对于我这个非酋 我真的比较服气我的脸 黑的像什么一样。学这个只是为了 考试遇到看似不可写的题目写一个随机化搜索。
毕竟 随机化到一定程度就可以完全的达到正确答案。
关于模拟退火 我只能说 真的是玄学 做题全靠随机。 随机 答案 随机AC 随机 都是随机 。
但是当随机到了一定次数 那么此时答案就有可能是最优解或者无限逼近最优解了哈。
爬山算法加退火,爬山基于greedy的思想 也是针对于单峰函数的做法,但是这有随机的靠近貌似没有什么大用。
我们可以直接三分找最值 准确高效。但是其还是非常有效的。

正解貌似是正交分解 我不是鬼才 我才不会写正交分解因为不会写。。。
考虑直接搜索答案 采用 模拟退火搜索 ,每次随机出一个值如果比当前优秀 就接受这个答案并以这个答案继续向后面搜索。
或者以一定的概率接受它 通常我们的写法是 exp((w-c)/T)>(db)rand()/RAND_MAX 如果是这样的话我们就接受它。
此时rand()的值就在0~RAND_MAX之间 RAND_MAX==32767没记错这个应该是short的最大范围吧。
而exp(x) 是返回以e为底的x次方 到这里就非常的玄学了 玄学的接受新解。
然后 生成解 的时候也是靠随机a=w1+T*(rand()*2-RAND_MAX); b=w2+T*(rand()*2-RAND_MAX);
生成在坐标范围内的 新坐标。 温度慢慢降低时 坐标的跳度也会降低这就是退火。能量降低。

//#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<string> #include<cstring> #include<ctime> #include<cmath> #include<queue> #include<stack> #include<algorithm> #include<cctype> #include<cstdlib> #include<utility> #include<iomanip> #include<vector> #include<deque> #include<set> #include<map> #include<bitset> #define INF 2147483646 #define min(x,y) (x>y?y:x) #define max(x,y) (x>y?x:y) #define up(p,i,n) for(int i=p;i<=n;++i) #define ll long long #define db double #define ldb long double #define x(i) t[i].x #define y(i) t[i].y #define w(i) t[i].w using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(int x) { x<0?putchar('-'),x=-x:0; int num=0;char ch[50]; while(x)ch[++num]=x%10,x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar(' ');return; } const int MAXN=1002; const double EPS=1e-14; int n; int ti=5; double ans,ansx,ansy; struct wy { int x,y; int w; }t[MAXN]; inline double carculate(double x,double y) { double tmp=0; up(1,i,n)tmp+=sqrt((x(i)-x)*(x(i)-x)+(y(i)-y)*(y(i)-y))*w(i); return tmp; } int main() { //freopen("1.in","r",stdin); n=read(); up(1,i,n) { x(i)=read(); y(i)=read(); w(i)=read(); ansx+=x(i); ansy+=y(i); } ansx/=n;ansy/=n; ans=carculate(ansx,ansy); srand(time(NULL)); while(ti--) { double w,w1,w2; w=ans;w1=ansx;w2=ansy; for(double T=10002;T>EPS;T*=0.98) { double a,b,c; a=w1+T*(rand()*2-RAND_MAX); b=w2+T*(rand()*2-RAND_MAX); c=carculate(a,b); if(ans>c)ans=c,ansx=a,ansy=b; if(w>c||exp((w-c)/T)>(db)rand()/RAND_MAX)w=c,w1=a,w2=b; } } printf("%.3lf %.3lf",ansx,ansy); return 0; }
调节好参数一般就能AC A不了也是80 看你是不是欧皇咯。

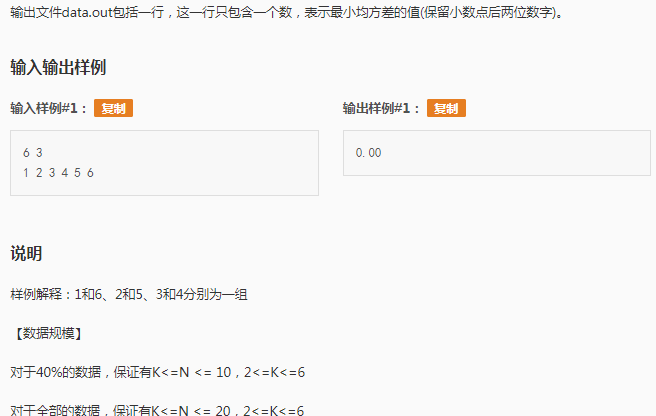
这道题就比较鬼畜一点了我调参调了1个多小时,关键是没有把握到随机的窍门 或者说我是太随机了。
初看题目好像40分能写爆搜 6^n 不会爆。 考虑随机化搜索,那么此时 我们随机化什么呢 标准差即均方差 貌似没用验证不了答案。
那考虑随机化数列 可是我根本没想出来可以随机化数列导致看了讨论才知道有 random_shuffle 这个玩意。
所以依靠它来进行 随机化数列即可 然后 取答案的时候显然靠dp 当然贪心解这道题会更轻松 然后我更没想到贪心。
然后发现是50分 因为random_shuffle 这玩意实在是太过于随机 很不容易随机到正解况且我的dp是完全按照随机到的东西来解当前序列来的到最优解的 所以这个不具有随机性 此时贪心针对每一个数字放在较小的那一组里根据随机性这个贪心贪的好 但是我要要随机到真正的答案 我要欧皇附体那就只能 以随机应随机了 此时我是太过于依赖这个 random_shuffle 了 其实已经脱离了模拟退火 开始胡蒙答案了 考虑 想模拟退火一样承接比较有优秀的状态 那就是 直接swap 直接swap 不就好了还能承接优秀的当前数列的情况 啊哈终于卡到了80 然后我也没有办法了 考修改随机种子 19260817 这玩意真好用直接AC 真猛 然后交bzoj 貌似不太行 bzoj 不认脸 那算了 我要让随机突破天际 于是随机多次 然后AC

//#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<string> #include<cstring> #include<ctime> #include<cmath> #include<queue> #include<stack> #include<algorithm> #include<cctype> #include<cstdlib> #include<utility> #include<iomanip> #include<vector> #include<deque> #include<set> #include<map> #include<bitset> #define INF 214748364 #define min(x,y) (x>y?y:x) #define max(x,y) (x>y?x:y) #define up(p,i,n) for(int i=p;i<=n;++i) #define ll long long #define db double #define ldb long double using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(int x) { x<0?putchar('-'),x=-x:0; int num=0;char ch[50]; while(x)ch[++num]=x%10,x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar(' ');return; } const int MAXN=22; const db ESP=1e-4; int n,k,flag; db a[MAXN],s[MAXN],b[MAXN]; db ans=INF,tmp,arrange; db f[MAXN][MAXN];//f[i][j] 表示前i个数字分成j组此时的方差值 inline void carculate() { up(1,i,n)s[i]=s[i-1]+a[i]; f[0][0]=0; up(1,i,n)up(1,j,k) { f[i][j]=INF; for(int w=j-1;w<=i;++w) { if((f[w][j-1]+(s[i]-s[w]-arrange)*(s[i]-s[w]-arrange))<f[i][j]) f[i][j]=f[w][j-1]+(s[i]-s[w]-arrange)*(s[i]-s[w]-arrange); } } tmp=f[n][k]/k; return; } inline void simulatedannealing() { double w=ans; for(db T=50000;T>ESP;T*=0.98) { int x=rand()%n+1,y=rand()%n+1; if(x==y)continue; swap(a[x],a[y]);flag=1; carculate(); if(ans>tmp)ans=tmp,flag=0; if(w>tmp||exp(w-tmp)/T>(db)rand()/RAND_MAX)w=tmp,flag=0; if(flag)swap(a[x],a[y]); } up(1,i,n) { int x=rand()%n+1,y=rand()%n+1; if(x==y)continue; swap(a[x],a[y]); } return; } int main() { //freopen("1.in","r",stdin); srand(time(NULL)); n=read();k=read(); up(1,i,n)a[i]=read(),arrange+=a[i]; arrange/=k; up(0,i,n)up(0,j,k)f[i][j]=INF; carculate(); if(ans>tmp)ans=tmp; simulatedannealing();//simulated 模拟 annealing 退火 simulatedannealing(); simulatedannealing(); simulatedannealing(); simulatedannealing(); simulatedannealing(); //random_shuffle(a+1,a+1+n); //up(1,i,n)cout<<a[i]<<' '; //cout<<ans<<endl; //cout<<sqrt(ans)<<endl; printf("%.2lf",sqrt(ans)); return 0; }
参数调的时候需要自己感受 因为参数调的越准确 越容易AC 当然这种玄学做法不知道提倡。
以下转自 flash hu 的博客:
众所周知,模拟退火最麻烦的地方在调参,只有合适的参数才能在一定的时间内很大概率跑出最优解。
蒟蒻的经验暂时还不足呢qwq,不过也随便谈谈吧。
首先,根据数据范围和精度要求,可以基本确定EPS的大小了,不过也需要尝试手动微调。
比较麻烦的是温度和变动率。首先不必顾虑,都开大一点,先把最优解跑出来。
然后,手动二分吧,注意每个二分的值要多跑几遍,因为模拟退火有偶然性,一次跑出最优解不代表大部分时候都能。
不过因为有两个量,还不能直接二分,应该二分套二分比较合适
update:考试的时候写提答,总结了一种方法:观察法
一边退火一边输出当前的温度、解等信息,通过观察大致感受一下解的降低速率
一般来说,如果解的降低速率比较均匀,跑出来的最优解也就好一些
不均匀的话,就调整参数,将解的降低速率较快的时间段的ΔTΔT变大一点,速率就能减慢一点。反之同理。
