题目要求的是 A+A2+...+Ak,而不是单个矩阵的幂。
那么可以构造一个分块的辅助矩阵 S,其中 A 为原矩阵,E 为单位矩阵,O 为0矩阵 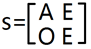
将 S 取幂,会发现一个特性:
Sk +1右上角那一块不正是我们要求的 A+A2+...+Ak
于是构造出 S 矩阵,然后对它求矩阵快速幂即可,最后别忘了减去一个单位阵。
时间降为O(n3log2k)
PS.减去单位矩阵的过程中要防止该位置小于零。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #define maxn 65 5 using namespace std; 6 struct mat{ 7 long long a[maxn][maxn]; 8 }; 9 mat res,c; 10 int n,k,m; 11 mat mat_mul(mat &x,mat &y,int Mod){ 12 mat ans; 13 memset(ans.a,0,sizeof(ans.a)); 14 for (int i=0;i<2*n;i++) 15 for (int j=0;j<2*n;j++) 16 for (int kk=0;kk<2*n;kk++){ 17 ans.a[i][j]+=x.a[i][kk]*y.a[kk][j]; 18 ans.a[i][j]%=Mod; 19 } 20 return ans; 21 } 22 void mat_pow(mat &res,int k,int Mod){ 23 mat c=res; 24 k--; 25 while (k){ 26 if (k&1) res=mat_mul(res,c,m); 27 k>>=1; 28 c=mat_mul(c,c,m); 29 } 30 } 31 int main(){ 32 cin >> n >> k >> m; 33 memset(res.a,0,sizeof(res.a)); 34 for (int i=0;i<n;i++){ 35 for (int j=0;j<n;j++){ 36 cin >> res.a[i][j]; 37 } 38 res.a[i][i+n]=res.a[i+n][i+n]=1; 39 } 40 mat_pow(res,k+1,m); //求出res的k+1次方 41 for (int i=0;i<n;i++){ 42 res.a[i][i+n]--; 43 while (res.a[i][i+n]<0) res.a[i][i+n]+=m; 44 } 45 for (int i=0;i<n;i++){ 46 for (int j=0;j<n-1;j++){ 47 cout << res.a[i][j+n] << " "; 48 } 49 cout << res.a[i][2*n-1] << endl; 50 } 51 return 0; 52 }