莫队
莫队算法的本质是一种暴力。
在一些区间(或树)上的问题,没有强制要求在线时,将区间(或树)上问题转换为离线去做。
1.普通莫队
算法介绍:
普通莫队,就是可离线,没有修改的莫队。这一类莫队算法的核心思想是:将整个数列区间划分$sqrt{n}$块。再将多个询问进行升序$sort()$,改变处理问题的顺序,即第一关键字为询问左区间l所在第几个块,第二关键字为询问右区间r。
用两个指针,$ll=1$和$rr=0$(保证开始为一个空区间)。从左到右处理所有询问。
在当前询问区间$[l_1,r_1]$向下一个询问区间$[l_2,r_2]$转移时,只需要处理两个指针在跳动过程中所经过的值就好。
核心代码:
1 ll=1,rr=0,cnt=0; 2 for (int i=0;i<m;i++){ 3 while (ll<b[i].l) del(ll++); 4 while (ll>b[i].l) add(--ll); 5 while (rr<b[i].r) add(++rr); 6 while (rr>b[i].r) del(rr--); 7 ans[b[i].id]=cnt; 8 }
复杂度:
用$B$代表块的大小。
对于$l$指针每次移动$O(B)$,对于指针$r$每次移动整个区间大小$O(n)$。
所以,对于$l$指针,移动次数最多为询问数×块的大小,即$O(m×B)$;
对于$r$指针,移动次数最多为块的个数×总区间大小,即$O(frac{n}{B}×n)$。
所以总的移动次数为:$O(m×B+frac{n}{B}×n)$。
可以看出这事一个对勾函数。
所以,当$B=sqrt{frac{n^2}{m}}$,即$B=frac{n}{sqrt{m}}$时,复杂度最小,为$O(nsqrt{m})$。
例.bzoj1878 [SDOI2009]HH的项链
传送:https://www.lydsy.com/JudgeOnline/problem.php?id=1878
题意:n个物品,每个物品有一个颜色,问区间$[l,r]$内有多少种颜色。
分析:莫队模板。

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxm=2e5+10; 4 const int maxn=5e4+10; 5 const int maxnum=1e6+10; 6 struct node{ 7 int l,r,blo,id; 8 bool operator <(node q)const{ 9 return blo<q.blo || blo==q.blo && r<q.r; 10 } 11 }b[maxm]; 12 int a[maxn],ans[maxm]; 13 int block,ll,rr,cnt; 14 int num[maxnum]; 15 void add(int x){ 16 int tmp=a[x]; 17 if (num[tmp]==0) cnt++; 18 num[tmp]++; 19 } 20 void del(int x){ 21 int tmp=a[x]; 22 if (num[tmp]==1) cnt--; 23 num[tmp]--; 24 } 25 int main(){ 26 int n; scanf("%d",&n); 27 block=sqrt(n); 28 for (int i=1;i<=n;i++) scanf("%d",&a[i]); 29 int m; scanf("%d",&m); 30 for (int i=0;i<m;i++){ 31 scanf("%d%d",&b[i].l,&b[i].r); 32 b[i].blo=b[i].l/block; 33 b[i].id=i; 34 } 35 sort(b,b+m); 36 memset(num,0,sizeof(num)); 37 ll=1,rr=0,cnt=0; 38 for (int i=0;i<m;i++){ 39 while (ll<b[i].l) del(ll++); 40 while (ll>b[i].l) add(--ll); 41 while (rr<b[i].r) add(++rr); 42 while (rr>b[i].r) del(rr--); 43 ans[b[i].id]=cnt; 44 } 45 for (int i=0;i<m;i++) printf("%d ",ans[i]); 46 return 0; 47 }
练习:
1.bzoj2038 小Z的袜子(hose)
传送:https://www.lydsy.com/JudgeOnline/problem.php?id=2038
题意:有n个袜子,每个袜子有一个颜色。m个询问,询问在一个区间$[l,r]$内,选择两种相同颜色的袜子的概率。
分析:莫队。将询问排序。每次转移时,$cnt$先减去$num[tmp]*num[tmp]$;更新$num$后,再加上$num[tmp]*num[tmp]$。最后的答案就是$cnt-b[i].len/b[i].len*(b[i].len-1)$。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn=5e4+10; 5 struct node{ 6 int l,r,blo,id; 7 bool operator <(node p)const{ 8 return blo<p.blo || blo==p.blo && r<p.r; 9 } 10 }b[maxn]; 11 struct node2{ 12 ll a,b; 13 }ans[maxn]; 14 int a[maxn]; 15 ll num[maxn]; 16 int ll_,rr_,block; 17 ll cnt; 18 void add(int x){ 19 int tmp=a[x]; 20 cnt-=num[tmp]*num[tmp]; 21 num[tmp]++; 22 cnt+=num[tmp]*num[tmp]; 23 } 24 void del(int x){ 25 int tmp=a[x]; 26 cnt-=num[tmp]*num[tmp]; 27 num[tmp]--; 28 cnt+=num[tmp]*num[tmp]; 29 } 30 ll calc(node p){ 31 return 1ll*(p.r-p.l+1)*(p.r-p.l); 32 } 33 ll gcd_(ll x,ll y){ 34 if (y==0) return x; 35 else return gcd_(y,x%y); 36 } 37 int main(){ 38 int n,m; scanf("%d%d",&n,&m); 39 block=sqrt(n); 40 for (int i=1;i<=n;i++) scanf("%d",&a[i]); 41 for (int i=0;i<m;i++){ 42 scanf("%d%d",&b[i].l,&b[i].r); 43 b[i].blo=b[i].l/block; 44 b[i].id=i; 45 } 46 sort(b,b+m); 47 ll_=1,rr_=0,cnt=0; 48 memset(num,0,sizeof(num)); 49 for (int i=0;i<m;i++){ 50 while (ll_<b[i].l) del(ll_++); 51 while (ll_>b[i].l) add(--ll_); 52 while (rr_<b[i].r) add(++rr_); 53 while (rr_>b[i].r) del(rr_--); 54 ans[b[i].id].a=cnt-(b[i].r-b[i].l+1); 55 ans[b[i].id].b=calc(b[i]); 56 } 57 for (int i=0;i<m;i++){ 58 ll tmp=gcd_(ans[i].a,ans[i].b); 59 ans[i].a/=tmp; ans[i].b/=tmp; 60 if (ans[i].a==0) printf("0/1 "); 61 else printf("%lld/%lld ",ans[i].a,ans[i].b); 62 } 63 return 0; 64 }
2.洛谷2709 小B的询问
题意:rt。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn=5e4+10; 5 struct node{ 6 int l,r,blo,id; 7 bool operator <(node p)const{ 8 return blo<p.blo || blo==p.blo && r<p.r; 9 } 10 }b[maxn]; 11 int a[maxn],num[maxn],l,r; 12 ll cnt; 13 ll ans[maxn]; 14 void add(int x){ 15 int tmp=a[x]; 16 cnt-=1ll*num[tmp]*num[tmp]; 17 num[tmp]++; 18 cnt+=1ll*num[tmp]*num[tmp]; 19 } 20 void del(int x){ 21 int tmp=a[x]; 22 cnt-=1ll*num[tmp]*num[tmp]; 23 num[tmp]--; 24 cnt+=1ll*num[tmp]*num[tmp]; 25 } 26 int main(){ 27 int n,m,k; scanf("%d%d%d",&n,&m,&k); 28 int block=sqrt(n); 29 for (int i=1;i<=n;i++) scanf("%d",&a[i]); 30 for (int i=0;i<m;i++){ 31 scanf("%d%d",&b[i].l,&b[i].r); 32 b[i].blo=b[i].l/block; 33 b[i].id=i; 34 } 35 sort(b,b+m); 36 l=1,r=0,cnt=0; 37 memset(num,0,sizeof(num)); 38 for (int i=0;i<m;i++){ 39 while (l<b[i].l) del(l++); 40 while (l>b[i].l) add(--l); 41 while (r<b[i].r) add(++r); 42 while (r>b[i].r) del(r--); 43 ans[b[i].id]=cnt; 44 } 45 for (int i=0;i<m;i++) printf("%lld ",ans[i]); 46 return 0; 47 }
2.带修莫队
算法介绍:
还是对询问进行排序,每个询问除了左端点和右端点还要记录这次询问是在第几次修改之后(时间),以左端点所在块为第一关键字,以右端点所在块为第二关键字,以时间为第三关键字进行排序。
暴力查询时,如果当前修改数比询问的修改数少就把没修改的进行修改,反之回退。
需要注意的是,修改分为两部分:
1.若修改的位置在当前区间内,需要更新答案(del原颜色,add修改后的颜色)。
2.无论修改的位置是否在当前区间内,都要进行修改(以供add和del函数在以后更新答案)。
核心代码:
1 while (l<b[i].l) del(l++); 2 while (l>b[i].l) add(--l); 3 while (r<b[i].r) add(++r); 4 while (r>b[i].r) del(r--); 5 while (tt<b[i].time) change(i,++tt); 6 while (tt>b[i].time) change(i,tt--); 7 ans[b[i].id]=cnt;
复杂度:
用$B$表示块的大小,$ccnt$代表修改次数,$qcnt$代表询问次数,$tt$代表当前的时间点,$l块$代表以左端点分的块,$r块$代表以右端点分的块。
对于指针$l$,在同一$l块$内每次最多移动$B$,跨$l块$块每次最多移动$2B$,总移动次数为$O(qcnt×B)$。
对于指针$r$,在同一$l块$块内,且在同一$r块$内,每次最多移动$B$,跨$r块$块每次最多移动$2B$,总移动次数为$O(qcnt×B)$;在跨$l块$块内,每次最多移动$n$,总移动次数为$O(n×frac{n^2}{B})$。所以最终总的移动次数为$O(qcnt×B+n×frac{n^2}{B})$。
对于时间指针$tt$,对于每个$r块$,最坏情况下移动$ccnt$次,总共有$(frac{n}{B})^2$个$r块$,所以总的移动次数为$frac{ccnt×n^2}{B^2}$。
所以总的移动次数为:$O(qcnt×B+n×frac{n^2}{B}+frac{ccnt×n^2}{B^2})$。
对于题目中,$qcnt$与$ccnt$的个数未知,都用$m$来表示,所以总的移动次数为:$O(m×B+n×frac{n^2}{B}+frac{mn^2}{B^2})$。
$B$的最佳取值为: 。
。
当$n==m$时,总的移动次数为:$O(n×B+n×frac{n^2}{B}+frac{n^3}{B^2})$,当$B=n^frac{2}{3}$时,取得最小值$O(n^frac{5}{3})$。
所以,带修莫队的时间复杂度为$O(nlogn+n^frac{5}{3})$。
例.洛谷1903[国家集训队]数颜色 / 维护队列
传送:https://www.luogu.org/problemnew/show/P1903
题意:n个物品,每个物品有一个颜色,m个操作。操作1:询问$[l,r]$内不同颜色的个数;操作2:将位置x的颜色修改为tmp。
分析:带修莫队模板。

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=5e4+10; 4 const int maxnum=1e6+5; 5 struct node{ 6 int l,r,id,time,lblo,rblo; 7 bool operator <(node p)const{ 8 return lblo<p.lblo || lblo==p.lblo && rblo<p.rblo 9 || lblo==p.lblo && rblo==p.rblo && time<p.time; 10 } 11 }b[maxn]; 12 struct node2{ 13 int x,tmp; 14 }c[maxn]; 15 int num[maxnum],ans[maxn],a[maxn]; 16 int l,r,cnt,qcnt,ccnt,tt,block; 17 void add(int x){ 18 int tmp=a[x]; 19 if (num[tmp]==0) cnt++; 20 num[tmp]++; 21 } 22 void del(int x){ 23 int tmp=a[x]; 24 if (num[tmp]==1) cnt--; 25 num[tmp]--; 26 } 27 void change(int i,int tt){ 28 if (c[tt].x>=b[i].l && c[tt].x<=b[i].r){ 29 //删除颜色 30 if (num[a[c[tt].x]]==1) cnt--; 31 num[a[c[tt].x]]--; 32 //添加颜色 33 if (num[c[tt].tmp]==0) cnt++; 34 num[c[tt].tmp]++; 35 } 36 swap(a[c[tt].x],c[tt].tmp); //回退 37 } 38 int main(){ 39 int n,m; scanf("%d%d",&n,&m); 40 block=pow(n,2.0/3); 41 for (int i=1;i<=n;i++) scanf("%d",&a[i]); 42 qcnt=0,ccnt=0; char ss[10]; 43 for (int i=0;i<m;i++){ 44 scanf("%s",ss); 45 if (ss[0]=='Q'){ 46 scanf("%d%d",&b[qcnt].l,&b[qcnt].r); 47 b[qcnt].lblo=b[qcnt].l/block; 48 b[qcnt].rblo=b[qcnt].r/block; 49 b[qcnt].id=qcnt; 50 b[qcnt++].time=ccnt; 51 } 52 else{ 53 ++ccnt; 54 scanf("%d%d",&c[ccnt].x,&c[ccnt].tmp); 55 } 56 } 57 sort(b,b+qcnt); 58 memset(num,0,sizeof(num)); 59 l=1,r=0,cnt=0,tt=0; 60 for (int i=0;i<qcnt;i++){ 61 while (l<b[i].l) del(l++); 62 while (l>b[i].l) add(--l); 63 while (r<b[i].r) add(++r); 64 while (r>b[i].r) del(r--); 65 while (tt<b[i].time) change(i,++tt); 66 while (tt>b[i].time) change(i,tt--); 67 ans[b[i].id]=cnt; 68 } 69 for (int i=0;i<qcnt;i++) printf("%d ",ans[i]); 70 return 0; 71 }
3.树上莫队
(小哲先去学LCA了!
算法介绍:
树上莫队,顾名思义,就是将莫队由序列挪至树上。
- 欧拉序:
核心思想是:当访问到点$i$时,加入序列,然后访问$i$的子树,当访问完时,再把$i$加入序列。
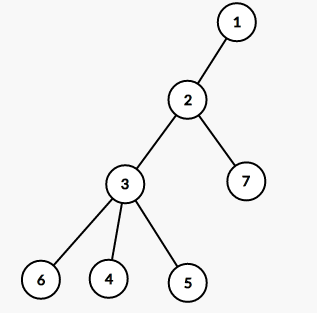
对于上图这棵树的欧拉序为:1 2 3 4 4 5 5 6 6 3 7 7 2 1
- LCA:
表示树上两结点之间的最近公共祖先。
树上莫队所求解的最经典(基础)问题为:求解树上$x$到$y$的唯一路径上出现了多少个不同的数。
这里设$st[i]$代表访问$i$时加入欧拉序的时间,$ed[i]$代表回溯经过$i$时加入欧拉序的时间。
假设:$st[x]<st[y]$,即先访问$x$,再访问$y$。
下面分情况讨论:
1.若$lca(x,y)=x$,这个时候代表$x,y$在同一条链上,那么在$st[x]$到$st[y]$的这段区间中,有的点经过了两次,有的点没有经过,这些点对答案没有贡献,只需要统计那些经过一次的点就可以了。
比如询问$2,6$时,$(st[2],st[6])=2 3 4 4 5 5 6$,4和5都出现了两次,不计入答案。
2.若$lca(x,y) epx$时,这个时候代表$x,y$在不同的子树里,同样按照上面的方法统计$ed[x]$到$st[y]$这段区间内的点就好。
比如询问$4,7$时,$(ed[4],et[7])=4 5 5 6 6 3 7$。
综上所述,我们需要特判两点之间的$lca$。
带修树上莫队
上面是不带修改的树上莫队。
带单点修改的树上莫队。
参考博客:https://www.cnblogs.com/ouuan/p/MoDuiTutorial.html
复杂度:
块的大小在$[B,3B)$,所以两点间的路径长度也在$[B,3B)$,块内移动是$O(B)$的。编号相邻的块位置相邻,之间路径长度也为$O(B)$。然后就与序列莫队一样。
例1。洛谷4618[SDOI2018]原题识别
传送:https://www.luogu.org/problemnew/show/P4618
题意:给定一个$n$个节点的树,每个节点表示一个整数,$m$个询问,问$u$到$v$的路径上有多少个不同的整数。
分析:树上莫队模板。
(辣鸡题目。。没有给$a[i]$范围,是$leq10^9$。需要把结点权值离散化再做。

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=4e5+10; 4 typedef pair<int,int> pii; 5 vector<int> mp[maxn]; 6 vector<pii> q[maxn]; 7 map<int,int> mp_; 8 int block,tot,num_,kk,cnt,ll,rr; 9 int ans[maxn],vis[maxn],fa[maxn],num[maxn],p[maxn]; 10 int st[maxn],ed[maxn],sta[maxn],bel[maxn],a[maxn],bb[maxn]; 11 struct node{ 12 int x,y,lca,blo,id; 13 bool operator <(node b)const { 14 return blo<b.blo || blo==b.blo && st[y]<st[b.y]; 15 } 16 }b[maxn]; 17 void dfs(int xx,int pre){ 18 st[xx]=++tot; p[tot]=xx; 19 int now=num_; 20 for (int i=0;i<mp[xx].size();i++){ 21 int tmp=mp[xx][i]; 22 if (tmp==pre) continue; 23 dfs(tmp,xx); 24 if (num_-now>=block){ 25 kk++; 26 while (num_!=now) bel[sta[num_--]]=kk; 27 } 28 } 29 sta[++num_]=xx; //入栈 30 ed[xx]=++tot; p[tot]=xx; 31 } 32 int find(int x){ 33 if (fa[x]==x) return x; 34 else return fa[x]=find(fa[x]); 35 } 36 void LCA(int root){ 37 fa[root]=root; 38 vis[root]=1; 39 for (int i=0;i<mp[root].size();i++){ 40 int tmp=mp[root][i]; 41 if (vis[tmp]) continue; 42 LCA(tmp); 43 fa[tmp]=root; 44 } 45 for (int i=0;i<q[root].size();i++){ 46 pii tmp=q[root][i]; 47 if (vis[tmp.first]){ 48 b[tmp.second].lca=find(tmp.first); 49 } 50 } 51 } 52 void add(int x){ 53 int tmp=a[x]; 54 num[tmp]++; 55 if (num[tmp]==1) cnt++; 56 } 57 void del(int x){ 58 int tmp=a[x]; 59 num[tmp]--; 60 if (num[tmp]==0) cnt--; 61 } 62 void update(int x){ 63 if (vis[x]) del(x); else add(x); 64 vis[x]^=1; 65 } 66 int main(){ 67 int n,m,x,y,l,r; scanf("%d%d",&n,&m); 68 block=sqrt(n); 69 for (int i=1;i<=n;i++){ 70 scanf("%d",&a[i]); 71 bb[i]=a[i]; 72 } 73 sort(bb+1,bb+1+n); 74 int kk=unique(bb+1,bb+1+n)-(bb+1); 75 for (int i=1;i<=kk;i++) mp_[bb[i]]=i; 76 for (int i=1;i<=n;i++) a[i]=mp_[a[i]]; //离散化 77 78 for (int i=0;i<n-1;i++){ 79 scanf("%d%d",&x,&y); 80 mp[x].push_back(y); 81 mp[y].push_back(x); 82 } 83 tot=0; num_=0; kk=0; 84 dfs(1,0); //处理欧拉序 85 while (num_) bel[sta[num_--]]=kk; 86 //for (int i=1;i<=tot;i++) cout << p[i] << " "; cout << endl; 87 88 for (int i=0;i<m;i++){ 89 scanf("%d%d",&b[i].x,&b[i].y); 90 if (st[b[i].x]>st[b[i].y]) swap(b[i].x,b[i].y); 91 b[i].blo=bel[b[i].x]; b[i].id=i; 92 q[b[i].x].push_back({b[i].y,i}); 93 q[b[i].y].push_back({b[i].x,i}); 94 } 95 memset(vis,0,sizeof(vis)); 96 LCA(1); 97 98 //莫队 99 sort(b,b+m); 100 ll=1,rr=0,cnt=0; 101 memset(num,0,sizeof(num)); 102 memset(vis,0,sizeof(vis)); 103 for (int i=0;i<m;i++){ 104 //cout << b[i].x << " " << b[i].y << endl; 105 int kk=b[i].lca; 106 if (kk==b[i].x){l=st[b[i].x]; r=st[b[i].y];} 107 else{l=ed[b[i].x]; r=st[b[i].y];} 108 //cout << l <<" " << r << endl; 109 while (ll<l) update(p[ll++]); 110 while (ll>l) update(p[--ll]); 111 while (rr<r) update(p[++rr]); 112 while (rr>r) update(p[rr--]); 113 if(kk!=b[i].x) update(kk); 114 ans[b[i].id]=cnt; 115 if(kk!=b[i].x) update(kk); 116 } 117 for (int i=0;i<m;i++) printf("%d ",ans[i]); 118 return 0; 119 }
例2。洛谷4074[WC2013]糖果公园
传送:https://www.luogu.org/problemnew/show/P4074
题意:给出一颗n个结点的树,每个结点上有一种糖果(糖果种类是$[q,m]$);
一个人经过结点$i$品尝糖果j获得的愉悦度为$w[time[j]]*val[j]$ (其中$time[j]$指$j$的品尝次数);
给出$q$次操作,操作有两种:1.更改某结点的糖果种类;2.查询某两个结点路径上的愉悦度总和。
分析:单点修改树上莫队。
