快速排序

快速排序

快速排序(Quick Sort)使用分治策略的排序算法，它的算法的基本步骤如下：

• 1.选择一个基准（需要注意的是基准的选择策略可能影响算法的性能）
• 2.通过一趟排序将待排序的序列分割成独立的两部分，其中前一部分记录的元素值比基准小，后一部分记录的元素值比基准大，这一步叫做分割
• 3.通过一趟排序此时基准的位置整好在其排好序的位置
• 4.分别对第2步得出的两部分进行同样的排序算法，之道整个序列有序

快排的图解

下面以数列a={30,40,60,10,20,50}为例，演示它的快速排序过程(如下图)。

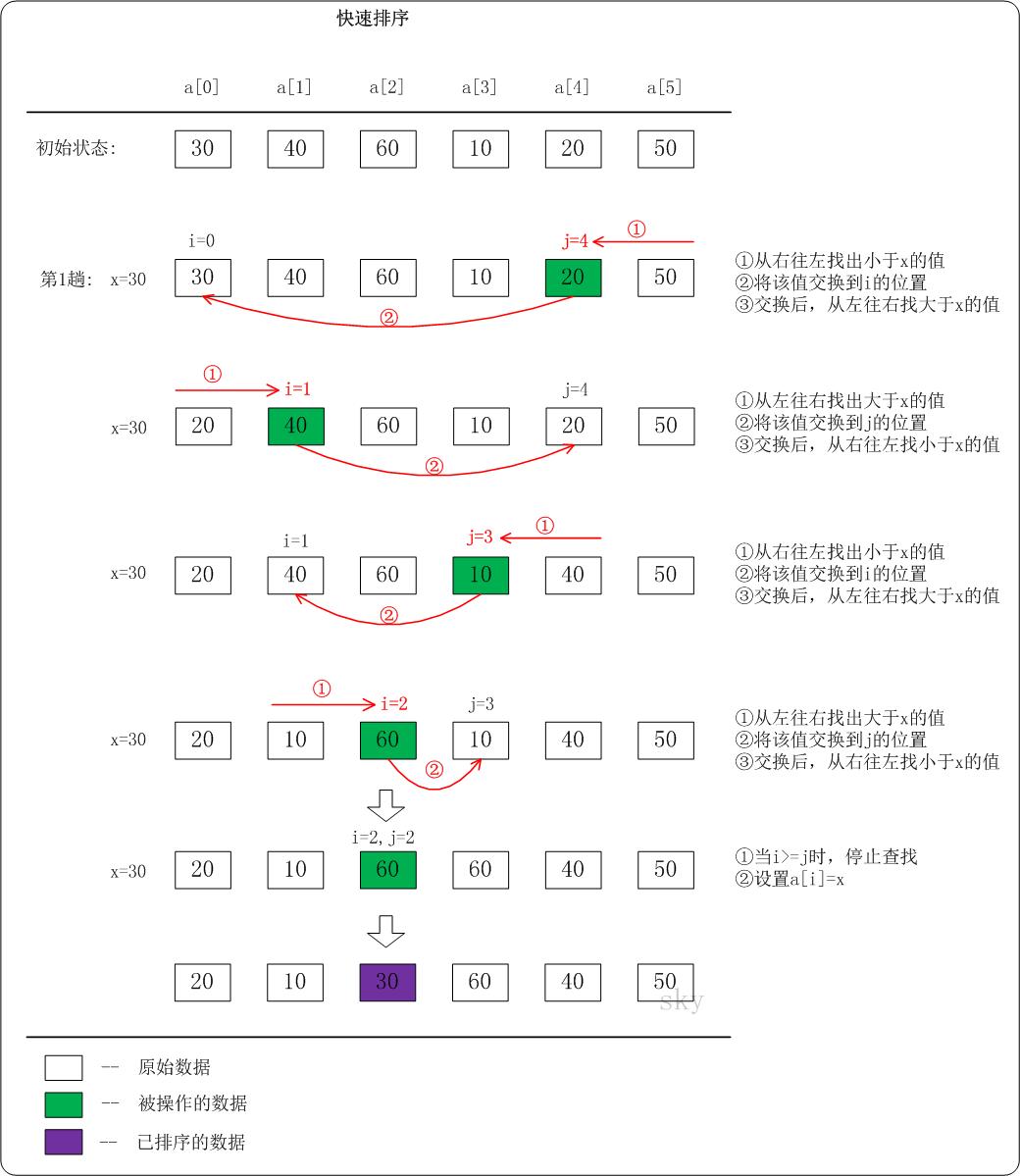
上图只是给出了第1趟快速排序的流程。在第1趟中，设置x=a[i]，即x=30。
(01) 从"右 --> 左"查找小于x的数：找到满足条件的数a[j]=20，此时j=4；然后将a[j]赋值a[i]，此时i=0；接着从左往右遍历。
(02) 从"左 --> 右"查找大于x的数：找到满足条件的数a[i]=40，此时i=1；然后将a[i]赋值a[j]，此时j=4；接着从右往左遍历。
(03) 从"右 --> 左"查找小于x的数：找到满足条件的数a[j]=10，此时j=3；然后将a[j]赋值a[i]，此时i=1；接着从左往右遍历。
(04) 从"左 --> 右"查找大于x的数：找到满足条件的数a[i]=60，此时i=2；然后将a[i]赋值a[j]，此时j=3；接着从右往左遍历。
(05) 从"右 --> 左"查找小于x的数：没有找到满足条件的数。当i>=j时，停止查找；然后将x赋值给a[i]。此趟遍历结束！

按照同样的方法，对子数列进行递归遍历。最后得到有序数组！

代码实现

/**
 * QuickSort
 */
public class QuickSort {

    public static void main(String[] args) {
        int[] array ={30,40,60,10,20,50};
        quickSort(array, 0, array.length-1);
        for (int i : array) {
            System.out.print(i + " ");
        }
    }
    public static void quickSort(int[] array, int start, int end) {
        if (start >= end) {
            return;
        }
        //
        int index = partation(array, start, end);   //获得基准位置
        //对两部分重复排序过程
        if (index > start) {
            quickSort(array, start, index-1);
        }
        if (index < end) {
            quickSort(array, index + 1, end);
        }
    }
    public static int partation(int[] array, int start, int end) {
        int i = start, j = end;
        int index = array[i];                       //确定基准
        while (i < j) {
            while (i < j && array[j] > index) {     //从右边找到第一个比基准小的
                j --;
            }
            if (i < j) {                            //移动元素到前面
                array[i++] = array[j];
            }
            while (i < j && array[i] < index) {     //从左到右找到第一个比基准大的
                i ++;
            }
            if (i < j) {                            //移动元素到后面
                array[j--] = array[i];
            }
        }
        array[i] = index;                           //放置基准的位置
        return i;
    }
}

快排分析

• 最坏时间复杂度
  最坏情况是指每次区间划分的时候，划分的结果都是在基准数字的左边或者右边的序列为空，另一边的序列的元素个数只比排序前少一项（很拗口）！！
  选择的基准是待排序的序列中最小或者最大的那一个！！ 此时的时间复杂度是O(n^2)。
• 最好时间复杂度
  最好情况是指每次区间划分的结果都是基准关键字左右两边的序列长度相等或者相差1，基准是待排序序列的中间值。此时的时间度复杂度是O(nlgn)。
• 平均时间复杂度
  时间度复杂度是O(nlgn)。
• 基准关键字的选取
  基准关键字的选取是决定算法性能的关键，常用的基准关键字选取方法如下：
  • 1. 三者取中
       三者取中是指在当前序列中将首、尾和中间的位置上的元素进行比较，选择三者的中值作为基准关键字，在划分开始前交换序列中第一个和基准关键字的位置。
  • 2. 取随机数
       取序列左边界和右边界之间的一个随机数作为基准关键字的位置，这种方法得到的快排叫做随机化快速排序。