冒泡排序

冒泡排序
冒泡排序是一种比较简单的排序算法。它会遍历若干次要排序的序列，每次排序的时候，它
都会从前往后比较相邻两个数的大小；如果前者比后者大，就交换他们的位置，这样一次遍
历之后，最大的元素就在数列的末尾！ 采用相同的方法再次遍历的时候，第二大的元素就
被排列在最大的元素之前。重复上述排列过程，直达整个数列排列完毕。
冒泡排序说明

import java.io.*;
class test  
{
    public static void BubbleSort(int[] array){
        int len = array.length;
        if( len <= 0)
            return;
        for (int i = len - 1; i >= 0 ; i-- ) {
            for(int j = 0; j < i; j ++){
                if(array[j] > array[j+1])
                swap(array, j, j+1);
            }
        } 
    }
    
    public static void swap(int[] array, int pos1, int pos2){
        int val = array[pos1];
        array[pos1] = array[pos2];
        array[pos2] = val;
    }
    public static void main (String[] args) { 
        int[] array = {20,40,30,10,60,50};
        BubbleSort(array);
        for(int i: array)
            System.out.println(i);
    }
}

下面以 {20,40,30,10,60,50}为例来说明：

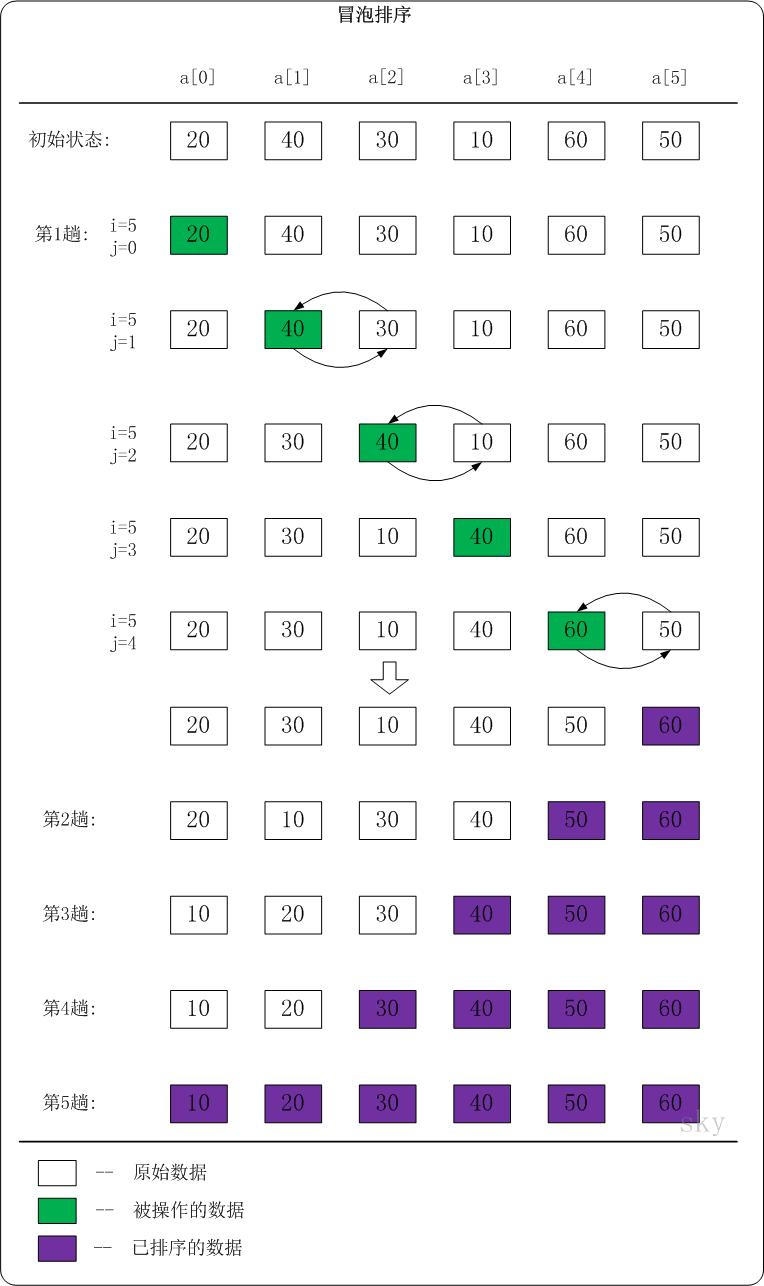
可以查看上图的排序过程：
第一趟排序选出了数组中最大的元素60，
第二趟排序选出了数组中对打的元素50，
∙∙∙∙∙∙∙
第五趟排序结束之后，整个数组就是有序的了。
但是从上图中，我们可以看到，其实在第三趟的时候，整个数组就已经完成了排序，第四趟
和第五趟并没有任何进行数据的交换，那么就可以对冒泡做一个简单的优化，增加一个标志
位，判断这一趟是否有数据的交换，如果没有那么就说明数组中数据已经排序完毕：

 public static void BubbleSortChange(int[] array) {
        int len = array.length;
        if( len <= 0)
            return;
        for (int i = len - 1; i >= 0 ; i-- ) {
            int flag = 0;
            for(int j = 0; j < i; j ++){
                if(array[j] > array[j+1]){
                    swap(array, j, j+1);
                    flag = 1;
                }
                   
            }
            if(flag == 0)
                break;
        } 
    }
    public static void swap(int[] array, int pos1, int pos2){
        int val = array[pos1];
        array[pos1] = array[pos2];
        array[pos2] = val;
    }

上面的排序实现的是从小到大的排序，那么从大到小怎么实现的，其实就是把上面的过程转
换：
第一趟遍历选出最小的那个，第二趟遍历选出次小的那个、、、、
直到n趟遍历完毕！！（变换一下中间的判断的符号）

 public static void BubbleSortChange(int[] array) {
        int len = array.length;
        if( len <= 0)
            return;
        for (int i = len - 1; i >= 0 ; i-- ) {
            int flag = 0;
            for(int j = 0; j < i; j ++){
                if(array[j] > array[j+1]){
                    swap(array, j, j+1);
                    flag = 1;
                }
                   
            }
            if(flag == 0)
                break;
        } 
    }
    public static void swap(int[] array, int pos1, int pos2){
        int val = array[pos1];
        array[pos1] = array[pos2];
        array[pos2] = val;
    }

冒泡排序的时间复杂度和稳定性
冒泡排序的时间复杂度是O(N2)。
假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢？N­1
次！因此，冒泡排序的时间复杂度是O(N2)。
冒泡排序稳定性
冒泡排序是稳定的算法，它满足稳定算法的定义。
算法稳定性 ­­ 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序
之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！