Python数据的相关性和标准化

1、相关性分析

协方差：Cov(X，Y)=E(XY)-E(X)E(Y) 或 cov(X, Y) = E(X-EX)(Y-EY)，表示两个变量总体误差的期望，范围在负无穷到正无穷。协方差为0时，两者独立。协方差绝对值越大，两者对彼此的影响越大，反之越小

公式简单翻译一下是：如果有X,Y两个变量，每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”得到一个乘积，再对这每时刻的乘积求和并求出均值（其实是求“期望”，但就不引申太多新概念了，简单认为就是求均值了）。

相关系数：（相关系数=协方差除以两个变量的标准差）的绝对值越大，相关性越强。衡量变量间的相关程度或密切程度，范围[-1,1]，分正负相关，负相关意味着两个变量的增长趋势相反。相关系数也可以看成协方差：一种剔除了两个变量量纲影响、标准化后的特殊协方差，单纯反应两个变量每单位变化时的相似程度。标准差描述了变量在整体变化过程中偏离均值的幅度。协方差除以标准差，也就是把协方差中变量变化幅度对协方差的影响剔除掉，这样协方差也就标准化了，它反应的就是两个变量每单位变化时的情况。（当x或y的波动幅度变大的时候，协方差会变大，标准差也会变大。）（在描述X和Y在同一物理量纲之下有一定的作用，但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异。因此统一单位，即消去x和y的单位，除以标准差，引入相关系数）

 

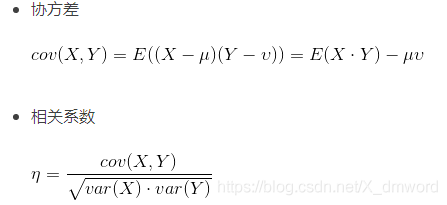
### 相关系数矩阵
import pandas as pd
data=pd.read_csv('E:/test.csv')
print(data.corr())  ## 两两之间的相关性
print(data.corr()[u'G3'])  ##G3与其他的相关系数
 
import numpy as np
import pandas as pd
data=pd.read_csv('E:/test.csv')
print(data.head())
correlation=np.corrcoef(data,rowvar=0) ##  0对列做分析，1对行做分析
## x=data.ix[:,:-1] #### 切分自变量，只讨论自变量间的相关性？？
## correlation=np.corrcoef(x,rowvar=0)  ### np.cov() 协方差
print(correlation.round(2))  ## 保留2位小数
## 输出相关矩阵，也是对称矩阵

和 numpy 相比，pandas 对于有多组数据的协方差、相关系数的计算比 numpy 更为简便、清晰，我们可以指定计算具体的两组数据的协方差、相关系数，这样就不需要再分析结果的协方差矩阵了。见参考
dfab = pd.DataFrame(ab.T, columns=['A', 'B'])
# A B 协方差
dfab.A.cov(dfab.B)
>> 150.95263157894738
# A B 相关系数
dfab.A.corr(dfab.B)

2、标准化

目的：处理不同规模和量纲的数据。使其缩放到相同的数据区间和范围，以减少规模、特征、分布差异等对模型的影响。

7个严格定义的基本单位是：长度（米）、质量（千克）、时间（秒）、电流（安培）、热力学温度（开尔文）、物质的量（摩尔）和发光强度（坎德拉），量纲即单位的组合。

1）Z-Score标准化：适合大多数类型的的数据，不适合稀疏数据（因为该方法是一种中心化方法，会改变原有数据的分布结构）。基于原始数据的均值和标准差，标准化后的数据是以0为均值，方差为1的正态分布。

                                 x'=(x-mean)/std

2）归一化的Max-Min标准化：对原始数据进行线性变换，得到的数据全部落在[0,1]区间，很好的保持原有数据结构。

                                 x'=(x-min)/(max-min)

3）MaxAbs（最大值绝对值标准化）：用于稀疏数据，不会破坏原有数据分布结构的特点，得到的数据会落在一定区间[-1,1]。

                                 x'=x/|max|，max为x所在列的最大的绝对值

import pandas as pd
import numpy as np
from sklearn import preprocessing
data=[[78,521,602,2865],[144,-600,-521,2245],[146,413,435,2571]]
df=pd.DataFrame(data)
## Z标准
zs=preprocessing.StandardScaler() ### 建立StandardScaler对象
df1=zs.fit_transform(data)
df1=np.round(df1,2)
 
## 最大-最小标准化
mm=preprocessing.MinMaxScaler() ### 建立MinMaxScaler
df2=mm.fit_transform(data)
df2=np.round(df2,2)
 
### 最大值绝对值标准化
mb=preprocessing.MaxAbsScaler() ### 建立MaxAbsScale
df3=mb.fit_transform(data)
df3=np.round(df3,2)
print(df,'

',df1,'

',df2,'

',df3)

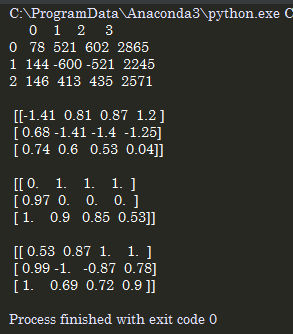
import pandas as pd
import numpy as np
data=[[78,521,602,2865],[144,-600,-521,2245],[146,413,435,2571]]
data=pd.DataFrame(data)
## Z标准
## 0表示列 1表示行
df1=(data - np.mean(data,axis=0))/ np.std(data,axis=0)
## df1=(data-data.mean(0))/data.std(0)   可能是pandas的统计量形式，结果不同
df1=np.round(df1,2)
 
## 最大-最小标准化
df2=(data -data.min(0)) / (data.max(0) - data.min(0)) 
df2=np.round(df2,2)
 
### 最大值绝对值标准化
df3=data/ abs(data).max(0)   ## 最大的绝对值
##df3=data/ abs(np.max(data,axis=0)) ## 最大值的绝对值
df3=np.round(df3,2)
print(data,'

',df1,'

',df2,'

',df3,)
##print(data.std(0))
##print(np.std(data,axis=0))

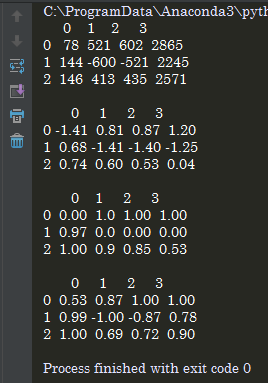
两个结果数值一样，注意numpy和pandas的统计量有所差异

两种做法的结果形式也有所差异，向量一维，数组矩阵多维，数据框类似表格
————————————————
版权声明：本文为CSDN博主「X_dmword」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/X_dmword/article/details/88700855