2019牛客暑期多校训练营（第十场） G Road Construction（计算几何、思维）

https://ac.nowcoder.com/acm/contest/890/G

题意

平面上有偶数个点，现在你要找出一条直线将这些点隔开成数量相同的两部分，直线不能穿过任何一点

问离直线最近的点离直线的距离最大是多少？

题解

必须知道一个结论：

这条最优的直线一定是与某两点连线平行或垂直。

那么我们可以枚举直线斜率n^2，然后求出所有点到这条直线的距离并排序nlogn，

那么中间的两个的差值除以2就是答案。

总时间复杂度n^3logn，n最大为300可以接受。

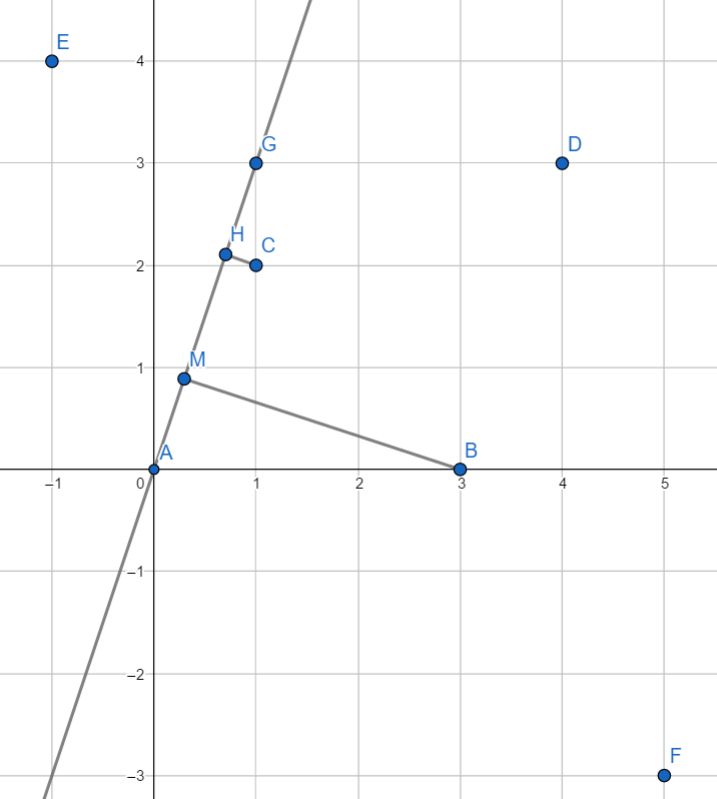
举个例子，如图（其实就是第一个样例），我们要把A,B,C,D,E,F分开，假设我们已经枚举到平行BD的直线AG，

那么答案为（BM-CH）/2。

代码很好写

#define bug(x) cout<<#x<<" is "<<x<<endl
#define IO std::ios::sync_with_stdio(0)
#include <bits/stdc++.h>
#define iter ::iterator
#define pa pair<int,ll>
using namespace  std;
#define ll long long
#define mk make_pair
#define pb push_back
#define se second
#define fi first
ll mod=998244353;
const int N=1e5+5;
int n;
struct node{
    double x,y;
}p[N];
double ans=0;
double d[N];
void cal(double k){
    for(int i=1;i<=n;i++){
        d[i]=(k*p[i].x-p[i].y)/sqrt(1+k*k);
    }
    sort(d+1,d+1+n);
    double res=(d[n/2+1]-d[n/2])/2;
    ans=max(ans,res);
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%lf%lf",&p[i].x,&p[i].y);
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<i;j++){
            double k=(p[i].y-p[j].y)/(p[i].x-p[j].x);
            cal(k);
            k=-1/k;
            cal(k);
        }
    }
    printf("%.10lf
",ans);
}