数据结构与算法——计数排序

原文链接：https://jiang-hao.com/articles/2020/algorithms-algorithms-count-sort.html

目录

• 算法介绍
• 算法实现
• 算法优化

算法介绍

计数排序（Counting sort）是一种稳定的线性时间排序算法。该算法于1954年由 Harold H. Seward 提出。计数排序使用一个额外的数组C ，其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。

当输入的元素是 n 个 0 到 k 之间的整数时，它的运行时间是 Θ(n + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法。

由于用来计数的数组C的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存。例如：计数排序是用来排序0到100之间的数字的最好的算法，但是它不适合按字母顺序排序人名。但是，计数排序可以用在基数排序中的算法来排序数据范围很大的数组。

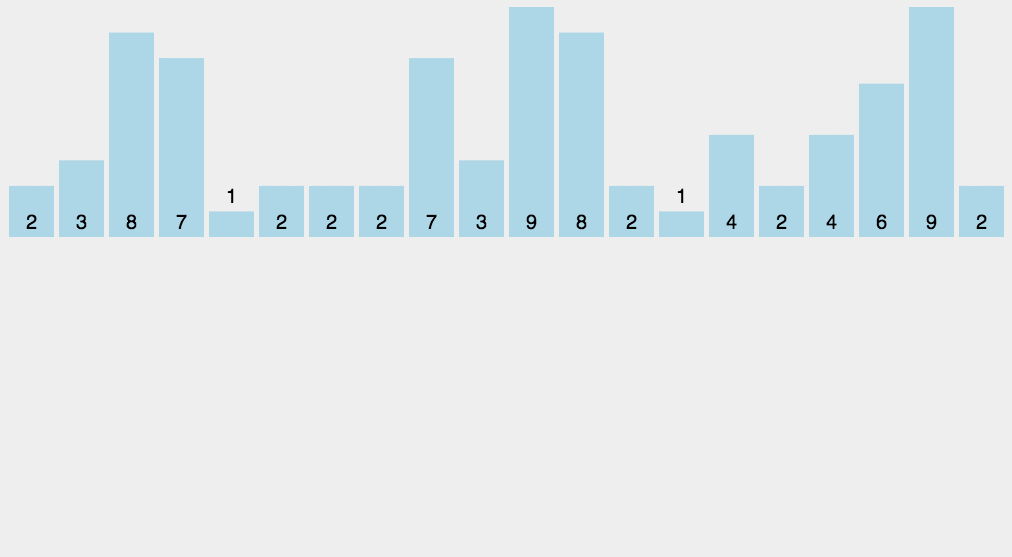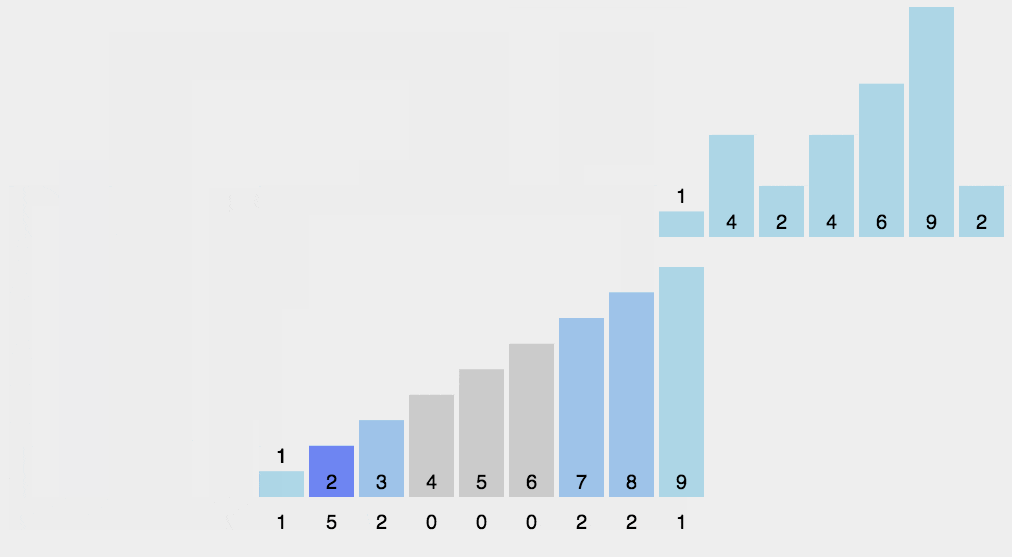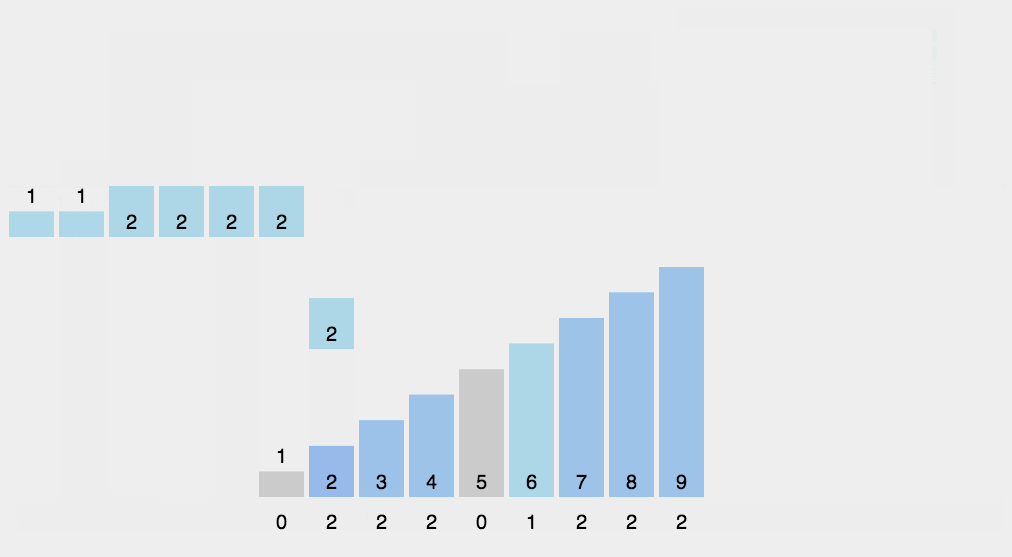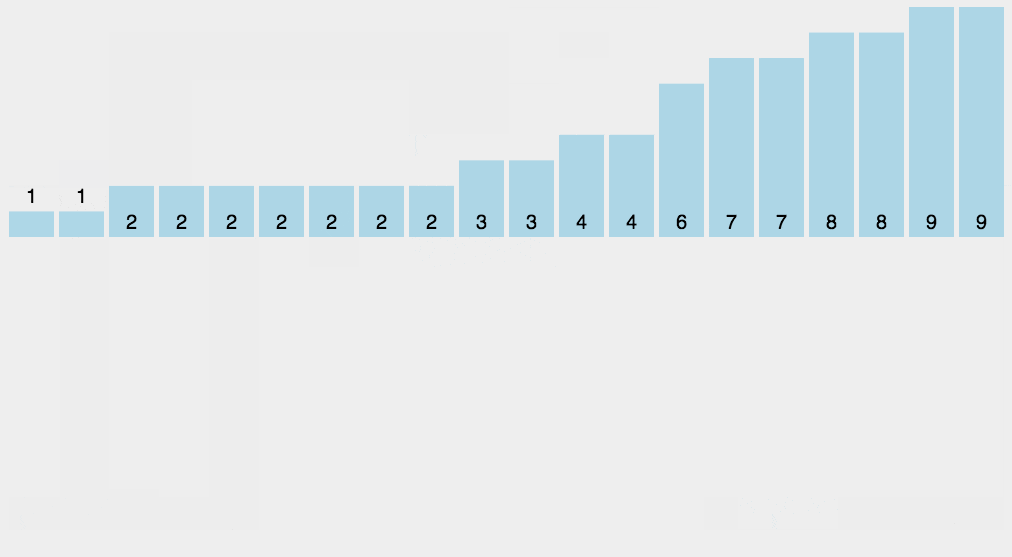
我们使用下面的例子进行说明。

假设有20个随机整数，其取值范围在0~10之间，对其进行排序，由于这20个随机整数的取值范围是固定的，那么我们可以定义一个长度为11的数组，数组下标为从0到10，并且元素初始值全为0，然后遍历要排序的20个随机整数，将遍历到的数值对应的数组下标进行+1，直到遍历结束。如下图所示：

假设我们要遍历的20个随机数为：9，3，5，4，8，9，1，2，7，8，5，3，6，7，9，0，4，7，2，4。创建一个长度为11的数组如下所示：

然后我们开始遍历，遍历的第一个数字是9，则给新建立的数组下标为9的值+1，即：

接着我们依此类推，直到遍历完要排序的数，遍历完之后的结果是：

根据上面的数组的结果，我们就可以得到一个有序的数列，即：0，1，2，2，3，3，4，4，4，5，5，6，7，7，7，8，8，9，9，9。

算法实现

public static int[] sort(int[] arr) {
    // 空数组直接返回
    if (arr.length==0) return arr;
    // 新建数组储存排序后的结果
    int[] res = new int[arr.length];
    // 得到数列的最大值
    int max = arr[0];
    for (int i: arr) {
        if (max < i) max = i;
    }
    // 根据数列最大值确定统计数组的长度
    int[] cntArr = new int[max+1];
    // 遍历数组，填充统计数组
    for (int i: arr) {
        cntArr[i]++;
    }
    // 遍历统计数组,得到排好序后的数组
    int index = 0;
    for (int i=0; i<cntArr.length; i++) {
        for (int j=0; j<cntArr[i]; j++) {
            res[index++] = i;
        }
    }
    return res;
}

算法优化

问题1：

对于上面的计数排序，我们不难发现存在这样一个问题：如果要排序的20个随机整数的范围在81~93之间，那么我们就需要建立一个长度为94的数组，这样就会造成新建的数组的前面81个空间位置就白白浪费了。

解决方法：

我们可以通过使用使用数列的最大值-最小值+1作为统计数组的长度即可，同时使用最小值作为一个偏移量，用于计算整数在统计数组中的下标。

问题2：

以上的计数排序只是按照输入数列从小到大的一个顺序对其进行输出而已，并没有对原始数列进行排序。如果遇到类似于对学生分数进行排序这样的现实问题，比如对于相同分数的学生就会造成分不清分数对应的是谁这样的问题。

解决方法：

假如现在有5个学生的分数为：（学生A：90，学生B：99，学生C：95，学生D：94，学生E：95），使用上面的方法得到的统计数组如下所示：

我们首先对统计数组进行变形，即从统计数组的第2个元素开始，每个元素都加上前面的所有元素之和，得到的新的统计数组如下所示：

然后，我们从后向前依次遍历5位学生的分数，第1个为学生E95分，找到统计数组下标为5的元素，值是4，代表学生E成绩排名在第4位，然后对数组下标为5的元素的值-1，表示下次再遇到成绩为95分的，其位置就会在第3位，按照此方法就会得出最终的成绩排名顺序为：（学生A：90，学生B：94，学生C：95，学生D：95，学生E：99）。

优化后的计数排序的实现：

public static int[] sort(int[] arr) {
    // 空数组直接返回
    if (arr.length==0) return arr;
    // 新建数组储存排序后的结果
    int[] res = new int[arr.length];
    // 得到数列的最大值，最小值
    int max = arr[0];
    int min = max;
    for (int i: arr) {
        if (max < i) max = i;
        if (min > i) min = i;
    }
    // 根据数列最大最小值确定统计数组的长度
    int[] cntArr = new int[max-min+1];
    // 遍历数组，填充统计数组
    for (int i: arr) cntArr[i-min]++;
    // 遍历统计数组累加计数
    for (int i=1; i<cntArr.length; i++) cntArr[i]+=cntArr[i-1];
    // 倒序遍历数组,得到排好序后的数组
    for (int i=arr.length-1; i>=0; i--) res[--cntArr[arr[i]-min]] = arr[i];
    return res;
}