[2017北航软工]第1次个人项目
——求解数独与生成数独终局
项目GitHub地址 https://github.com/Hesitater/Sudoku
解题思路
这次的数独问题主要可分为求解数独与生成终局两大部分。最开始拿到题目的时候,我决定先完成生成终局,再求解数独,然而找到的大部分生成数独的算法都无法满足生成1000000个不同终局的要求。虽然初始决策的错误让我绕了一些弯路,但也让我拜识不同生成终局的算法,在这里将找到的终局生成算法贴出来:
前两个算法用的都是对已有终局进行行、列、单元格交换的生成方法,最后一个算法比较有特色,虽然也需要终局,但相较前两者加入了一定随机性。
求解数独
在发现先生成终局这条路走不通后,我改变了策略,选择先完成求解数独的功能。在谷歌求解算法的过程中,翻到了Ladit同学的这篇博客:深度优先搜索和回溯法生成数独。我最后采用了博客中推荐的DLX算法来求解数独。由于使用指针操作以及算法解法的巧妙,DLX算法算是数独求解算法当中效率较高的,以下是对DLX算法讲解得比较全面而又易懂的两篇博客:
生成终局
生成终局同样利用求解数独的DLX算法就能完成。如果将DLX算法看做一个函数,求解数独的过程就是把挖了空的终局作为参数传给函数,让函数把空位填满;生成终局的过程就是把没有数字的空数独(除了第一个格子被填上指定数字)作为参数传给函数,让函数把空位填满。
这篇博客也提供了一个DLX和深度优先搜索结合的方式生成数独。这个算法给数独生成增加了一定随机性而又能保证生成的终局数量,值得参考——产生数独谜题
整体设计
类结构:
一共有8各类,可分为两大部分:
-
DLX:
-
- DLXNode——DLX节点类
-
- ColumnHead——DLXNode子类,列头类
-
- CommonNode——DLXNode子类,普通节点类
-
- DLXGenerator——DLX十字链表创建类
-
- DLXSolver——DLX问题求解类
-
-
Sudoku:
-
- SudokuLoader——文件存取操作类
-
- SudokuSolver——数独求解类,以DLXSolver为核心
-
- SudokuGenerator——终局生成类
-
代码组织:
数独的求解与终局生成都是建立在DLX算法的基础上的,因此为DLX算法单独设立了5个类来管理DLX算法,明确各部分分工。
单元测试:
贴出程序的两个重要方法的测试
SudokuSolver::solveSudoku:测试解出的数独是否与答案相符
TEST_METHOD(TestSolveSudoku) {
vector<int> puzzleVector;
vector<int> solutionVector;
int puzzle[81] = {
0,1,2,3,4,0,7,8,9,
7,8,9,5,1,2,3,4,6,
3,4,6,7,8,9,5,1,2,
2,5,1,0,3,4,9,6,7,
6,9,7,2,5,1,8,3,4,
8,3,4,6,9,7,2,5,0,
1,2,5,4,7,3,6,9,8,
9,6,8,0,2,5,4,7,3,
4,7,3,9,6,8,1,2,0 };
vector solution[81] = {
5,1,2,3,4,6,7,8,9,
7,8,9,5,1,2,3,4,6,
3,4,6,7,8,9,5,1,2,
2,5,1,8,3,4,9,6,7,
6,9,7,2,5,1,8,3,4,
8,3,4,6,9,7,2,5,1,
1,2,5,4,7,3,6,9,8,
9,6,8,1,2,5,4,7,3,
4,7,3,9,6,8,1,2,5
};
for (int i = 0; i < 81; i++) {
puzzleVector.push_back(puzzle[i]);
}
SudokuSolver solver;
DLXNode* listHead = new DLXNode();
solver.solveSudoku(listHead, puzzleVector, solutionVector);
for (int j = 0; j < 81; ++j) {
Assert::AreEqual(solutionVector[i], solution[i]);
}
}
SudokuGenerator::generate: 测试生成的数独是否满足数独的约束与格式
TEST_METHOD(TestGenerateSudokus) {
SudokuSolver solver;
DLXNode* listHead = new DLXNode();
vector<vector<int>> sudokus;
vector<int> answers;
SudokuGenerator generator;
generator.generateSudokus(10);
for (int i = 0; i < 10; ++i) {
Assert::AreEqual(solver.solveSudoku(listHead, sudokus[i], answers),true);
}
}
性能分析
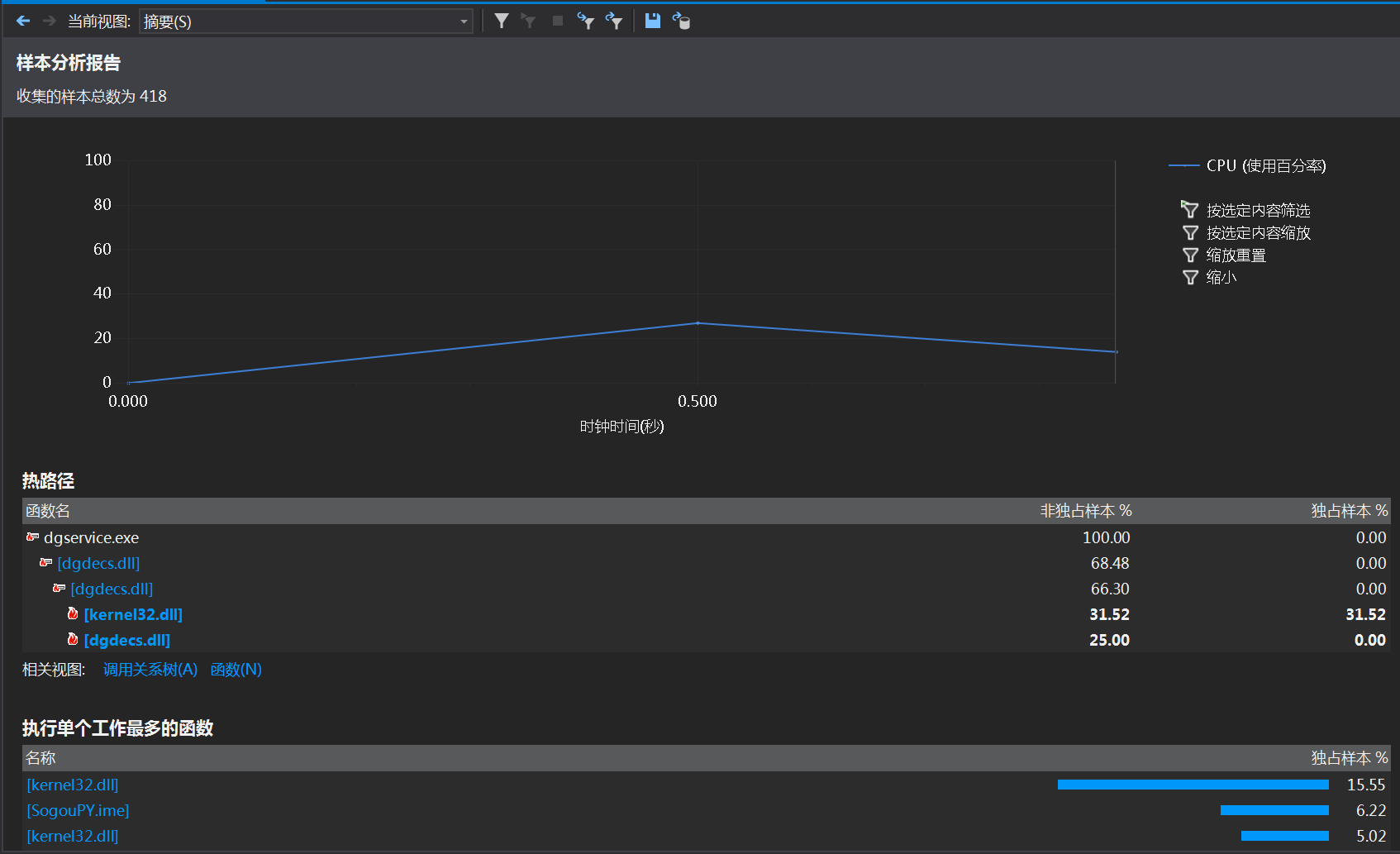
上图为VS生成的本次项目的样本分析报告

从上面的调用树可以看出,整个程序占用资源最多的方法是SudokuSolver::solveWithMultiAnswers,这个方法主要负责利用DLX算法完成求解工作,暂时未想到性能改进的办法。
代码说明
DLX部分:
DLXGenerator::appendLine:增加一行元素到DLX十字链表底部
void DLXGenerator::appendLine(vector<ColumnHead*> columnHeads, vector<int> elementSubscripts, int rowIndex){
CommonNode* lastHorizontalNode = NULL;
CommonNode* firstHorizontalNode = NULL;
for (int i = 0; i < elementSubscripts.size(); ++i) {
int subscript = elementSubscripts[i];
ColumnHead* columnHead = columnHeads[subscript];
CommonNode* currentNode = new CommonNode(rowIndex, columnHead);
DLXNode *lastVerticalNode = columnHead->upNode;
//Link vertical nodes
lastVerticalNode->appendDownNode(currentNode);
currentNode->appendDownNode(columnHead);
//Link horizontal nodes
if (i == 0) {
firstHorizontalNode = currentNode;
lastHorizontalNode = currentNode;
} else {
lastHorizontalNode->appendRightNode(currentNode);
lastHorizontalNode = currentNode;
}
currentNode->columnIndex = columnHead->columnIndex;
columnHead->numberOfOne++;
}
lastHorizontalNode->appendRightNode(firstHorizontalNode);
}
DLXSolver::solveWithOneAnswer:求解DLX十字链(只求一个解),参数listHead为DLX十字链链头,solution中存储所有解的行号。
bool DLXSolver::solveWithOneAnswer(DLXNode *listHead, vector<int>& solution, int depth) {
if (listHead->rightNode == listHead) { //Solution found
/*for (int i = 0; i < depth; ++i) { //Debugging code
cout << solution[i] <<endl;
}*/
return true;
}
//Select column with least one's
ColumnHead* columnHead = selectColumn(listHead);
cover(columnHead);
bool solutionFound = false; //Usage: return type
//Loop rows with one in column below columnHead
for (DLXNode* node = columnHead->downNode; node != columnHead; node = node->downNode) {
solution.push_back(((CommonNode*)node)->rowIndex); //Add temporary tempSolution node
for (DLXNode* node2 = node->rightNode; node2 != node; node2 = node2->rightNode) {
cover(((CommonNode*)node2)->columnHead);
}
depth++;
solutionFound = solveWithOneAnswer(listHead, solution, depth); //Enter next recursion level
depth--;
for (DLXNode* node2 = node->leftNode; node2 != node; node2 = node2->leftNode) {
uncover(((CommonNode*)node2)->columnHead);
}
if (solutionFound){ //Solution found, jump out loop
break;
}
solution.pop_back(); //Delete temporary tempSolution node
}
uncover(columnHead);
return solutionFound;
}
DLXSolver:: solveWithCertainAnswers:对一个DLX十字链表,求多(answerCount)个解
void DLXSolver:: solveWithCertainAnswers(DLXNode *listHead, vector<int>& tempSolution, vector<vector<int>>& lastSolution,
int answerCount, int depth) {
if (listHead->rightNode == listHead) { //One solution found
/*for (int i = 0; i < depth; ++i) { //Debugging code
cout << tempSolution[i] <<endl;
}*/
lastSolution.push_back(tempSolution);
return;
}
ColumnHead* columnHead = selectColumn(listHead);
cover(columnHead);
for (DLXNode* node = columnHead->downNode; node != columnHead; node = node->downNode) {
tempSolution.push_back(((CommonNode*)node)->rowIndex); //Add temporary tempSolution node
for (DLXNode* node2 = node->rightNode; node2 != node; node2 = node2->rightNode) {
cover(((CommonNode*)node2)->columnHead);
}
depth++;
solveWithCertainAnswers(listHead, tempSolution, lastSolution, answerCount, depth); //Enter next recursion level
depth--;
for (DLXNode* node2 = node->leftNode; node2 != node; node2 = node2->leftNode) {
uncover(((CommonNode*)node2)->columnHead);
}
if (lastSolution.size() == answerCount) { //Solution count achieved get out of recursion
break;
}
tempSolution.pop_back(); //Delete temporary tempSolution node
}
uncover(columnHead);
return;
}
Sudoku部分:
SudokuSolver::solveSudoku:得到所给数独题的一个解,传到answer中
void SudokuSolver::solveSudoku(DLXNode *listHead, vector<int> &sudoku, vector<int> &answer) {
transformToList(sudoku, listHead);
DLXSolver dlxSolver = DLXSolver();
vector<int> solution;
dlxSolver.solveWithOneAnswer(listHead, solution, 0); //Got DLX answer
solutionToAnswer(solution, answer); //Answer got
}
SudokuSolver::solveWithMultiAnswers:对一个数独题求多(answercount)个解
* void SudokuSolver::solveWithMultiAnswers(DLXNode *listHead, vector<int>& sudoku, vector<vector<int>>& answers, int answerCount) {
transformToList(sudoku, listHead);
DLXSolver dlxSolver = DLXSolver();
vector<int> tempSolution;
vector<vector<int>> lastSolution;
dlxSolver.solveWithCertainAnswers(listHead, tempSolution, lastSolution, answerCount, 0); //Got DLX answer
//Get answers from lastSolution
for (int i = 0; i < answerCount; ++i) {
vector<int> answer;
solutionToAnswer(lastSolution[i], answer);
answers.push_back(answer);
}
}
SudokuGenerator:: generateSudokus:创建sudokuCount个不重复的终局
vector<vector<int>> SudokuGenerator:: generateSudokus(int sudokuCount) {
vector<vector<int>> answers;
//Create an sudoku with all zero
vector<int> originalSudoku;
for (int j = 0; j < sudokuSize; ++j) {
if (j == 0) { //The first one must be 5
originalSudoku.push_back(5);
}else {
originalSudoku.push_back(0);
}
}
//Solve the zero sudoku to get sudoku outcomes
DLXGenerator generator = DLXGenerator();
DLXNode* listHead = new DLXNode();
SudokuSolver solver = SudokuSolver();
solver.solveWithMultiAnswers(listHead, originalSudoku, answers, sudokuCount);
return answers;
}
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 5 | 7 |
| · Estimate | · 估计这个任务需要多少时间 | 5 | 7 |
| Development | 开发 | 430 | 1020 |
| · Analysis | · 需求分析 (包括学习新技术) | 120 | 600 |
| · Design Spec | · 生成设计文档 | 30 | 0 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 0 | 0 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 0 |
| · Design | · 具体设计 | 20 | 120 |
| · Coding | · 具体编码 | 120 | 120 |
| · Code Review | · 代码复审 | 10 | 0 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 120 | 180 |
| Reporting | 报告 | 70 | 160 |
| · Test Report | · 测试报告 | 30 | 30 |
| · Size Measurement | · 计算工作量 | 10 | 5 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 125 |
| 合计 | 505 | 1207 |
小结
万事开头难。由于对语法、算法和各种工具的生疏,这次的项目花了不少时间,Deadline前才勉强把作业的基本要求达成。这一周的练习算是让我头次真正体会到高效学习的重要性,打算在下次项目尝试指定阶段性目标,可把一周的项目周期切割成三份,每个项目制定周期定为2~4天,希望能对效率提高有所帮助。