HNOI2008 水平可见直线

传送门

这道题我自己想了想……不过并没有想出什么很好的方法。

我们简单一点考虑，问题可以转化成求所有在最上面的直线的那个集合中有哪些直线。我们知道斜率最大（接近正无穷）和斜率最小（接近负无穷）的是肯定要被保留下来的，而且还是在最两侧的两条直线。

那么对于一般的直线，我们考虑一下。

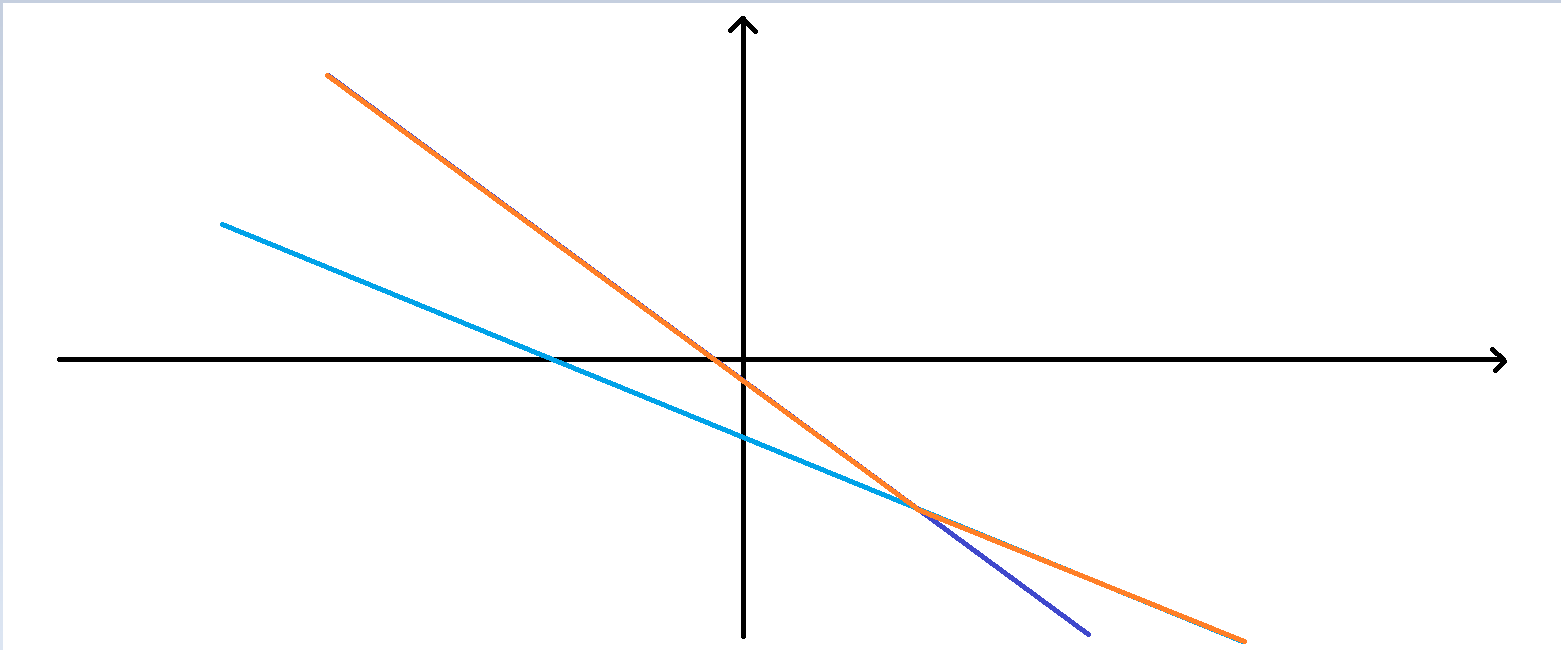
如上图，这两条直线都是可见的。那么再插入一条新的直线，就会变成这个样子：

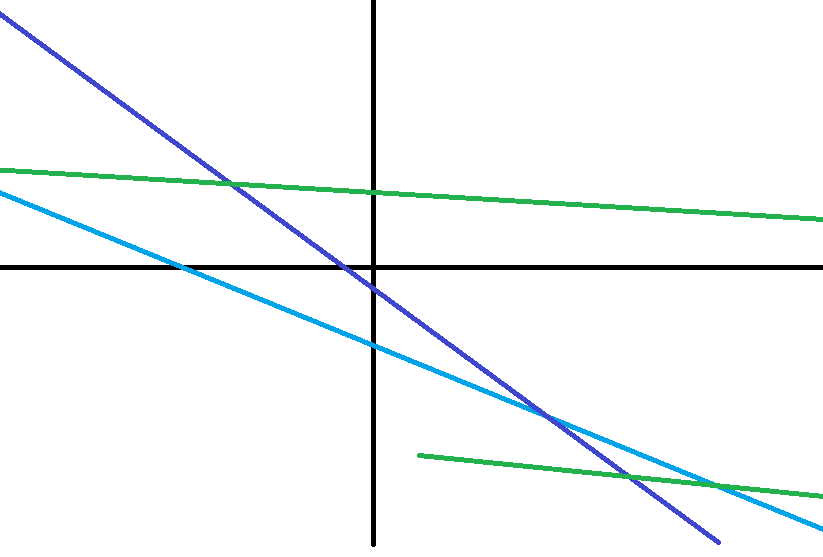
这样的话，可以发现对于斜率更大的一条线，如果他与当前斜率最大的线的交点在斜率最大和次大的直线交点的左侧，那么当前斜率最大的直线会被覆盖，我们应该使用新的直线去代替这条直线，而如果是在右侧，那么我们就把它保留下来即可。

这样似乎思路就很清晰了。我们把直线按照斜率从小到大排序（当然反过来也一样），之后使用单调栈来维护当前可以被看见的直线有哪些，每次遇到一条新的，斜率更大的直线，我们把它和栈顶元素的交点计算出来，再把栈顶元素和栈中第二个元素的交点计算出来，之后按照上面的方法处理单调栈就好。

然后，对于有多条直线斜率相同的情况，肯定是去取截距最大的那一条（下面的一定被它覆盖了），所以我们可以重载个运算符，按想要的方式排序就好。

交点只需要计算横坐标，直接连立求解就可以啦。

看一下简短的代码。

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#define rep(i,a,n) for(int i = a;i <= n;i++)
#define per(i,n,a) for(int i = n;i >= a;i--)
#define enter putchar('
')
using namespace std;
typedef long long ll;
const int M = 200005;

int read()
{
    int ans = 0,op = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-') op = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        ans *= 10;
        ans += ch - '0';
        ch = getchar();
    }
    return ans * op;
}    
struct node
{
    int a,b,id;
    bool operator < (const node &g) const
    {
        if(a == g.a) return b > g.b;
        return a > g.a;
    }
}line[M];
double solve(int p,int q)//计算交点位置
{
    return (double)(line[p].b - line[q].b) / (double)(line[q].a - line[p].a);
}
int n,stack[M],top,ans[M];
int main()
{
    n = read();
    rep(i,1,n) line[i].a = read(),line[i].b = read(),line[i].id = i;
    sort(line+1,line+1+n);
    rep(i,1,n)
    {
        if(line[i].a == line[i-1].a && i != 1) continue;//斜率相同的情况
        while(top > 1 && solve(stack[top],i) >= solve(stack[top],stack[top-1])) top--;//将不合法元素从栈中清除
        stack[++top] = i;//将元素压入栈
        ans[top] = line[i].id;    
    }
    sort(ans,ans+top+1);//把答案排个序
    rep(i,1,top) printf("%d ",ans[i]);
    return 0;
}