Imp likes his plush toy a lot.

Recently, he found a machine that can clone plush toys. Imp knows that if he applies the machine to an original toy, he additionally gets one more original toy and one copy, and if he applies the machine to a copied toy, he gets two additional copies.
Initially, Imp has only one original toy. He wants to know if it is possible to use machine to get exactly x copied toys and y original toys? He can't throw toys away, and he can't apply the machine to a copy if he doesn't currently have any copies.
The only line contains two integers x and y (0 ≤ x, y ≤ 109) — the number of copies and the number of original toys Imp wants to get (including the initial one).
Print "Yes", if the desired configuration is possible, and "No" otherwise.
You can print each letter in arbitrary case (upper or lower).
Examples
input 6 3 output Yes
input 4 2 output No
input 1000 1001 output Yes
In the first example, Imp has to apply the machine twice to original toys and then twice to copies.
思路:注意很多特殊情况,漏掉就会gg。
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int x,y; int main(){ scanf("%d%d",&x,&y); x-=(y-1); if(x==0&&y==1){ cout<<"Yes";return 0; } if(x>=0&&x%2==0&&y>1) cout<<"Yes"; else cout<<"No"; }
Imp is in a magic forest, where xorangles grow (wut?)

A xorangle of order n is such a non-degenerate triangle, that lengths of its sides are integers not exceeding n, and the xor-sum of the lengths is equal to zero. Imp has to count the number of distinct xorangles of order n to get out of the forest.
Formally, for a given integer n you have to find the number of such triples (a, b, c), that:
- 1 ≤ a ≤ b ≤ c ≤ n;
 , where
, where 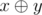 denotes the bitwise xor of integers x and y.
denotes the bitwise xor of integers x and y.- (a, b, c) form a non-degenerate (with strictly positive area) triangle.
The only line contains a single integer n (1 ≤ n ≤ 2500).
Print the number of xorangles of order n.
Examples
input 6 output 1
input 10 output 2
The only xorangle in the first sample is (3, 5, 6).
思路:枚举即可,注意两个相同的数的抑或值为0。
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int n,ans; int main(){ scanf("%d",&n); for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++){ int k=i^j; if(k>n) continue; if(i+j>k&&abs(i-j)<k&&i+k>j&&abs(i-k)<j&&j+k>i&&abs(j-k)<i) ans++; } cout<<ans/3; }
Imp is watching a documentary about cave painting.

Some numbers, carved in chaotic order, immediately attracted his attention. Imp rapidly proposed a guess that they are the remainders of division of a number n by all integers i from 1 to k. Unfortunately, there are too many integers to analyze for Imp.
Imp wants you to check whether all these remainders are distinct. Formally, he wants to check, if all 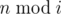 , 1 ≤ i ≤ k, are distinct, i. e. there is no such pair (i, j) that:
, 1 ≤ i ≤ k, are distinct, i. e. there is no such pair (i, j) that:
- 1 ≤ i < j ≤ k,
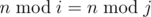 , where
, where 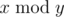 is the remainder of division x by y.
is the remainder of division x by y.
Input
The only line contains two integers n, k (1 ≤ n, k ≤ 1018).
Output
Print "Yes", if all the remainders are distinct, and "No" otherwise.
You can print each letter in arbitrary case (lower or upper).
Examples
input 4 4 output No
input 5 3 output Yes
In the first sample remainders modulo 1 and 4 coincide.
思路:正序顺序枚举就可以了。
#include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int vis[1000000]; long long n,k; int main(){ cin>>n>>k; for(int i=1;i<=k;i++){ int m=n%i; if(!vis[m]) vis[m]=1; else{ cout<<"No";return 0; } } cout<<"Yes"; }
Apart from plush toys, Imp is a huge fan of little yellow birds!

To summon birds, Imp needs strong magic. There are n trees in a row on an alley in a park, there is a nest on each of the trees. In the i-th nest there are ci birds; to summon one bird from this nest Imp needs to stay under this tree and it costs him costi points of mana. However, for each bird summoned, Imp increases his mana capacity by B points. Imp summons birds one by one, he can summon any number from 0 to ci birds from the i-th nest.
Initially Imp stands under the first tree and has W points of mana, and his mana capacity equals W as well. He can only go forward, and each time he moves from a tree to the next one, he restores X points of mana (but it can't exceed his current mana capacity). Moving only forward, what is the maximum number of birds Imp can summon?
The first line contains four integers n, W, B, X (1 ≤ n ≤ 103, 0 ≤ W, B, X ≤ 109) — the number of trees, the initial points of mana, the number of points the mana capacity increases after a bird is summoned, and the number of points restored when Imp moves from a tree to the next one.
The second line contains n integers c1, c2, ..., cn (0 ≤ ci ≤ 104) — where ci is the number of birds living in the i-th nest. It is guaranteed that 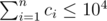 .
.
The third line contains n integers cost1, cost2, ..., costn (0 ≤ costi ≤ 109), where costi is the mana cost to summon a bird from the i-th nest.
Print a single integer — the maximum number of birds Imp can summon.
Examples
input 2 12 0 4 3 4 4 2 output 6
input 4 1000 10 35 1 2 4 5 1000 500 250 200 output 5
input 2 10 7 11 2 10 6 1 output 11

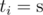 and
and 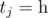 .
.


 for some set of integers
for some set of integers 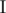 as the number of pairs
as the number of pairs 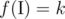 .
.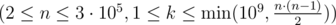 .
.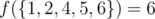 .
.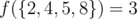 .
.