Python——因子分析（KMO检验和Bartlett's球形检验）

因子分析用Python做的一个典型例子

一、实验目的

采用合适的数据分析方法对下面的题进行解答

二、实验要求

采用因子分析方法，根据48位应聘者的15项指标得分，选出6名最优秀的应聘者。

三、代码

import pandas as pd
import numpy as np
import math as math
import numpy as np
from numpy import *
from scipy.stats import bartlett
from factor_analyzer import *
import numpy.linalg as nlg
from sklearn.cluster import KMeans
from matplotlib import cm
import matplotlib.pyplot as plt
def main():
    df=pd.read_csv("./data/applicant.csv")
    # print(df)
    df2=df.copy()
    print("
原始数据:
",df2)
    del df2['ID']
    # print(df2)

    # 皮尔森相关系数
    df2_corr=df2.corr()
    print("
相关系数:
",df2_corr)

    #热力图
    cmap = cm.Blues
    # cmap = cm.hot_r
    fig=plt.figure()
    ax=fig.add_subplot(111)
    map = ax.imshow(df2_corr, interpolation='nearest', cmap=cmap, vmin=0, vmax=1)
    plt.title('correlation coefficient--headmap')
    ax.set_yticks(range(len(df2_corr.columns)))
    ax.set_yticklabels(df2_corr.columns)
    ax.set_xticks(range(len(df2_corr)))
    ax.set_xticklabels(df2_corr.columns)
    plt.colorbar(map)
    plt.show()

    # KMO测度
    def kmo(dataset_corr):
        corr_inv = np.linalg.inv(dataset_corr)
        nrow_inv_corr, ncol_inv_corr = dataset_corr.shape
        A = np.ones((nrow_inv_corr, ncol_inv_corr))
        for i in range(0, nrow_inv_corr, 1):
            for j in range(i, ncol_inv_corr, 1):
                A[i, j] = -(corr_inv[i, j]) / (math.sqrt(corr_inv[i, i] * corr_inv[j, j]))
                A[j, i] = A[i, j]
        dataset_corr = np.asarray(dataset_corr)
        kmo_num = np.sum(np.square(dataset_corr)) - np.sum(np.square(np.diagonal(A)))
        kmo_denom = kmo_num + np.sum(np.square(A)) - np.sum(np.square(np.diagonal(A)))
        kmo_value = kmo_num / kmo_denom
        return kmo_value

    print("
KMO测度:", kmo(df2_corr))

    # 巴特利特球形检验
    df2_corr1 = df2_corr.values
    print("
巴特利特球形检验:", bartlett(df2_corr1[0], df2_corr1[1], df2_corr1[2], df2_corr1[3], df2_corr1[4],
                                  df2_corr1[5], df2_corr1[6], df2_corr1[7], df2_corr1[8], df2_corr1[9],
                                  df2_corr1[10], df2_corr1[11], df2_corr1[12], df2_corr1[13], df2_corr1[14]))

    # 求特征值和特征向量
    eig_value, eigvector = nlg.eig(df2_corr)  # 求矩阵R的全部特征值，构成向量
    eig = pd.DataFrame()
    eig['names'] = df2_corr.columns
    eig['eig_value'] = eig_value
    eig.sort_values('eig_value', ascending=False, inplace=True)
    print("
特征值
：",eig)
    eig1=pd.DataFrame(eigvector)
    eig1.columns = df2_corr.columns
    eig1.index = df2_corr.columns
    print("
特征向量
",eig1)

    # 求公因子个数m,使用前m个特征值的比重大于85%的标准，选出了公共因子是五个
    for m in range(1, 15):
        if eig['eig_value'][:m].sum() / eig['eig_value'].sum() >= 0.85:
            print("
公因子个数:", m)
            break

    # 因子载荷阵
    A = np.mat(np.zeros((15, 5)))
    i = 0
    j = 0
    while i < 5:
        j = 0
        while j < 15:
            A[j:, i] = sqrt(eig_value[i]) * eigvector[j, i]
            j = j + 1
        i = i + 1
    a = pd.DataFrame(A)
    a.columns = ['factor1', 'factor2', 'factor3', 'factor4', 'factor5']
    a.index = df2_corr.columns
    print("
因子载荷阵
", a)
    fa = FactorAnalyzer(n_factors=5)
    fa.loadings_ = a
    # print(fa.loadings_)
    print("
特殊因子方差:
", fa.get_communalities())  # 特殊因子方差，因子的方差贡献度 ，反映公共因子对变量的贡献
    var = fa.get_factor_variance()  # 给出贡献率
    print("
解释的总方差（即贡献率）:
", var)

    # 因子旋转
    rotator = Rotator()
    b = pd.DataFrame(rotator.fit_transform(fa.loadings_))
    b.columns = ['factor1', 'factor2', 'factor3', 'factor4', 'factor5']
    b.index = df2_corr.columns
    print("
因子旋转:
", b)

    # 因子得分
    X1 = np.mat(df2_corr)
    X1 = nlg.inv(X1)
    b = np.mat(b)
    factor_score = np.dot(X1, b)
    factor_score = pd.DataFrame(factor_score)
    factor_score.columns = ['factor1', 'factor2', 'factor3', 'factor4', 'factor5']
    factor_score.index = df2_corr.columns
    print("
因子得分：
", factor_score)
    fa_t_score = np.dot(np.mat(df2), np.mat(factor_score))
    print("
应试者的五个因子得分：
",pd.DataFrame(fa_t_score))

    # 综合得分
    wei = [[0.50092], [0.137087], [0.097055], [0.079860], [0.049277]]
    fa_t_score = np.dot(fa_t_score, wei) / 0.864198
    fa_t_score = pd.DataFrame(fa_t_score)
    fa_t_score.columns = ['综合得分']
    fa_t_score.insert(0, 'ID', range(1, 49))
    print("
综合得分：
", fa_t_score)
    print("
综合得分：
", fa_t_score.sort_values(by='综合得分', ascending=False).head(6))

    plt.figure()
    ax1=plt.subplot(111)
    X=fa_t_score['ID']
    Y=fa_t_score['综合得分']
    plt.bar(X,Y,color="#87CEFA")
    # plt.bar(X, Y, color="red")
    plt.title('result00')
    ax1.set_xticks(range(len(fa_t_score)))
    ax1.set_xticklabels(fa_t_score.index)
    plt.show()

    fa_t_score1=pd.DataFrame()
    fa_t_score1=fa_t_score.sort_values(by='综合得分',ascending=False).head()
    ax2 = plt.subplot(111)
    X1 = fa_t_score1['ID']
    Y1 = fa_t_score1['综合得分']
    plt.bar(X1, Y1, color="#87CEFA")
    # plt.bar(X1, Y1, color='red')
    plt.title('result01')
    plt.show()

if __name__ == '__main__':
    main()

 

四、实验步骤

（1）引入数据，数据标准化

因为数据是面试中的得分，量纲相同，并且数据的分布无异常值，所以数据可以不进行标准化。

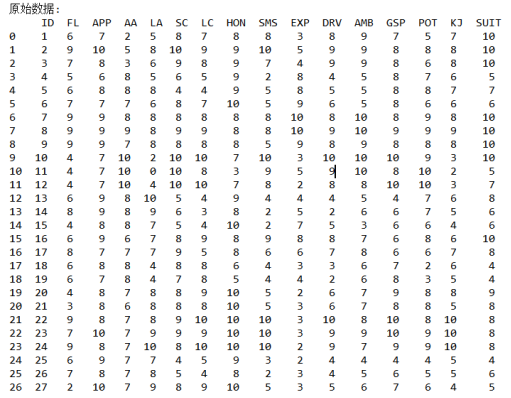
（2）建立相关系数矩阵

计算皮尔森相关系数，从热图中可以明显看出变量间存在的相关性。

 

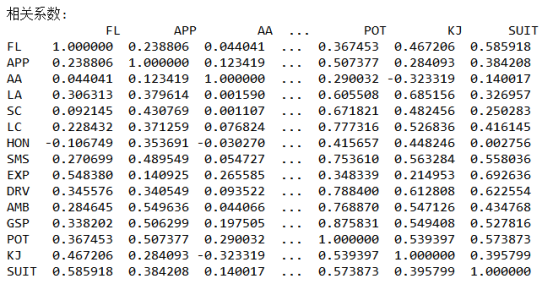
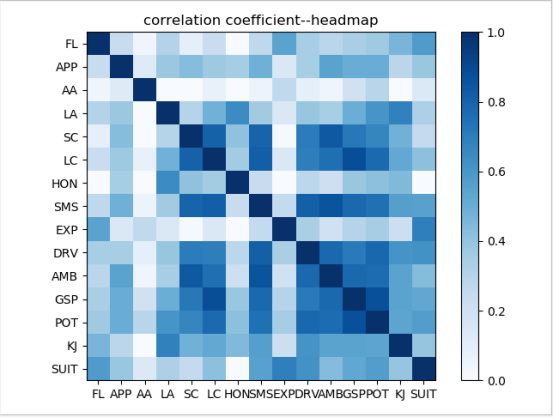
进行相关系数矩阵检验——KMO测度和巴特利特球体检验：

KMO值：0.9以上非常好；0.8以上好；0.7一般；0.6差；0.5很差；0.5以下不能接受；巴特利球形检验的值范围在0-1，越接近1，使用因子分析效果越好。

通过观察上面的计算结果，可以知道，KMO值为0.783775605643526，在较好的范围内，并且巴特利球形检验的值接近1，所有可以使用因子分析。

（3）求解特征值及相应特征向量 

 

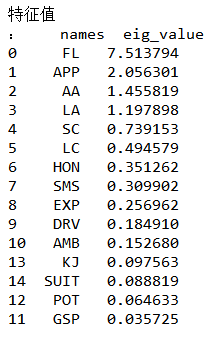
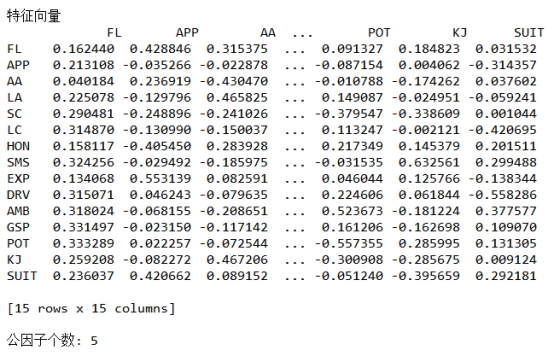
求公因子个数m,使用前m个特征值的比重大于85%的标准，选出了公共因子是五个。

（4）因子载荷阵

  

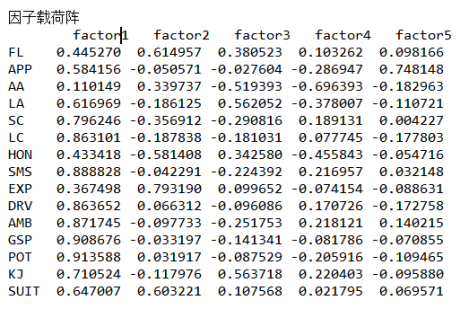
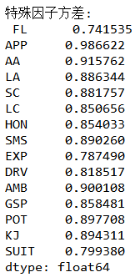
由上可以看出，选择5个公共因子，从方差贡献率可以看出，其中第一个公因子解释了总体方差的50.092%，四个公共因子的方差贡献率为86.42%，可以较好的解释总体方差。

（5）因子旋转

 

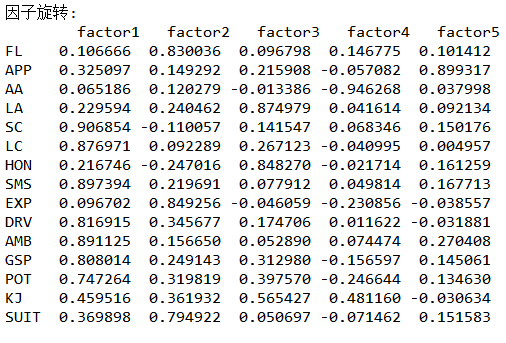
（6）因子得分

 

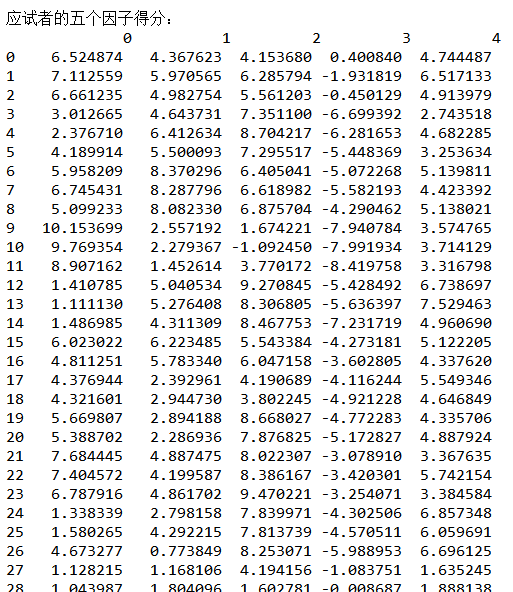
（7）根据应聘者的五个因子得分，按照贡献率进行加权，得到最终各应试者的综合得分，然后选出前六个得分最高的应聘者。

 

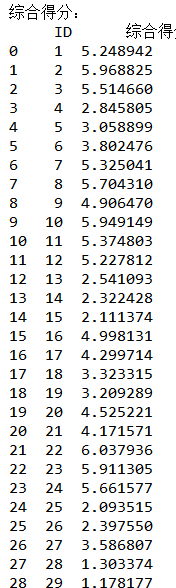
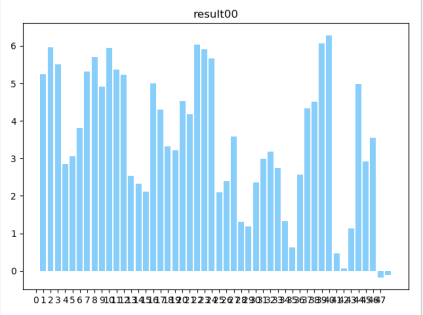
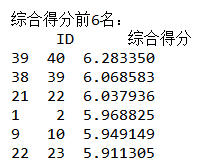
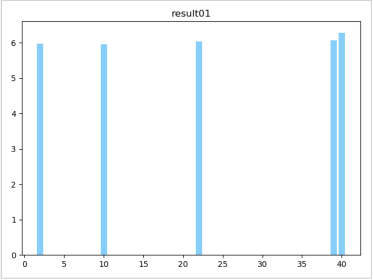
所以我们用因子分析产生的前六名分别是：40，39，22，2，10，23