简单回归
数据来源:http://www.statsci.org/data/general/cofreewy.html


1.读入数据
setwd("D:/数学建模/寒假美赛集训/R统计")
w=read.table("COfreewy.txt",header=T,encoding = "utf-8")
2.线性回归
a=lm(CO~.,w) #a=lm(CO~Traffic+Wind,w)#线性回归 #print(w) summary(a)
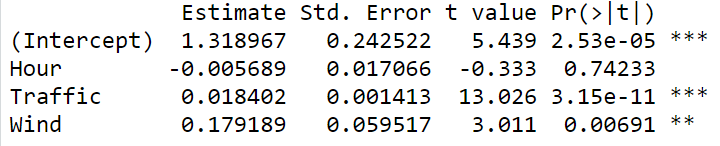
第一列为回归系数,第二列为标准差,一般都<0.05较好,第四列为p值。原假设为:系数为0。p<0.05,则拒绝原假设。若p>0.05,可以考虑去除该变量再做一次回归,以使每一个p值都<0.05。
3.AIC逐步回归
b=step(a,direction = "backward")#逐步回归 summary(b)
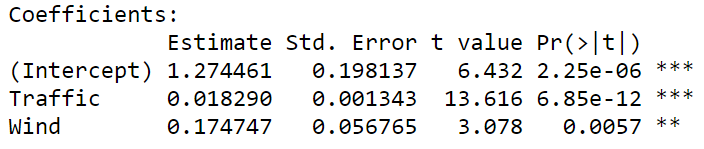
通过使用逐步回归,我们选择了变量,舍弃了Hour变量,每一个p值都<0.05。

4.残差检验
shapiro.test(b$res)#做残差的正态性检验
$y-hat{y}$为残差,应符合正态分布,均值为0。如果均值不为0,则存在系统误差。
5.画出qq图
qqnorm(b$res);qqline(b$res)#查看回归残差的qq图
qq图有两个作用:1、检验一组数据是否服从某一分布。2、检验两个分布是否服从同一分布。qq图全称是quantile-quantile plot,从名称中可以了解到是和分位数相关的图。qq图没有过原点,说明仍存在一定系统误差。


6.各变量散点图
plot(w) #pairs(w)
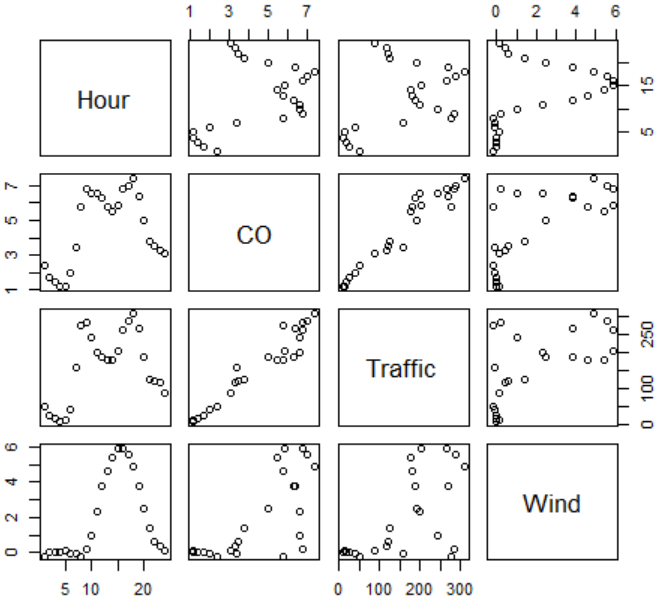
7.傅里叶技术变换

cor(cbind(CO,Traffic,Tsq=Traffic^2,Tcub=Traffic^3,
Hour,Hsq=Hour^2,Hcub=Hour^3,Wind,Wsq=Wind^2,Wcub=Wind^3))
a=lm(CO~Traffic+Wind+I(Wind^2)+I(Wind^3)+sin((2*pi/24)*Hour)+
cos((2*pi/24)*Hour)+sin((4*pi/24)*Hour)+cos((4*pi/24)*Hour))
b=step(a) #逐步回归,按照aIC选择变量
summary(b);anova(b);shapiro.test(b$res)
b1=lm(CO~Traffic+Wind+I(Wind^2)+
cos((2*pi/24)*Hour)+cos((4*pi/24)*Hour))
summary(b1)
anova(b1)#方差分析表
shapiro.test(b1$res)#对残差的正态性检验
qqnorm(b$res);qqline(b$res)#查看回归残差的qq图



所有代码:
setwd("D:/数学建模/寒假美赛集训/R统计")
w=read.table("COfreewy.txt",header=T,encoding = "utf-8")
attach(w)#把数据变成全局变量
print(CO)
head(w)#查看前6条数据
a=lm(CO~.,w)
#a=lm(CO~Traffic+Wind,w)#线性回归
#print(w)
summary(a)
b=step(a,direction = "backward")#逐步回归
summary(b)
shapiro.test(b$res)#做残差的正态性检验
qqnorm(b$res);qqline(b$res)#查看回归残差的qq图
par(mfrow=c(2,3))#同时显示6张图
plot(Traffic,Wind)
plot(CO,Wind)
plot(Traffic,CO)
plot(Hour,Wind)
plot(CO,Hour)
plot(Hour,Traffic)
plot(w)
#pairs(w)
cor(cbind(CO,Traffic,Tsq=Traffic^2,Tcub=Traffic^3,
Hour,Hsq=Hour^2,Hcub=Hour^3,Wind,Wsq=Wind^2,Wcub=Wind^3))
a=lm(CO~Traffic+Wind+I(Wind^2)+I(Wind^3)+sin((2*pi/24)*Hour)+
cos((2*pi/24)*Hour)+sin((4*pi/24)*Hour)+cos((4*pi/24)*Hour))
b=step(a) #逐步回归,按照aIC选择变量
summary(b);anova(b);shapiro.test(b$res)
b1=lm(CO~Traffic+Wind+I(Wind^2)+
cos((2*pi/24)*Hour)+cos((4*pi/24)*Hour))
summary(b1)
anova(b1)#方差分析表
shapiro.test(b1$res)#对残差的正态性检验
par(mfrow=c(1,1))
qqnorm(b$res);qqline(b$res)#查看回归残差的qq图