

> #############6.2一元线性回归分析
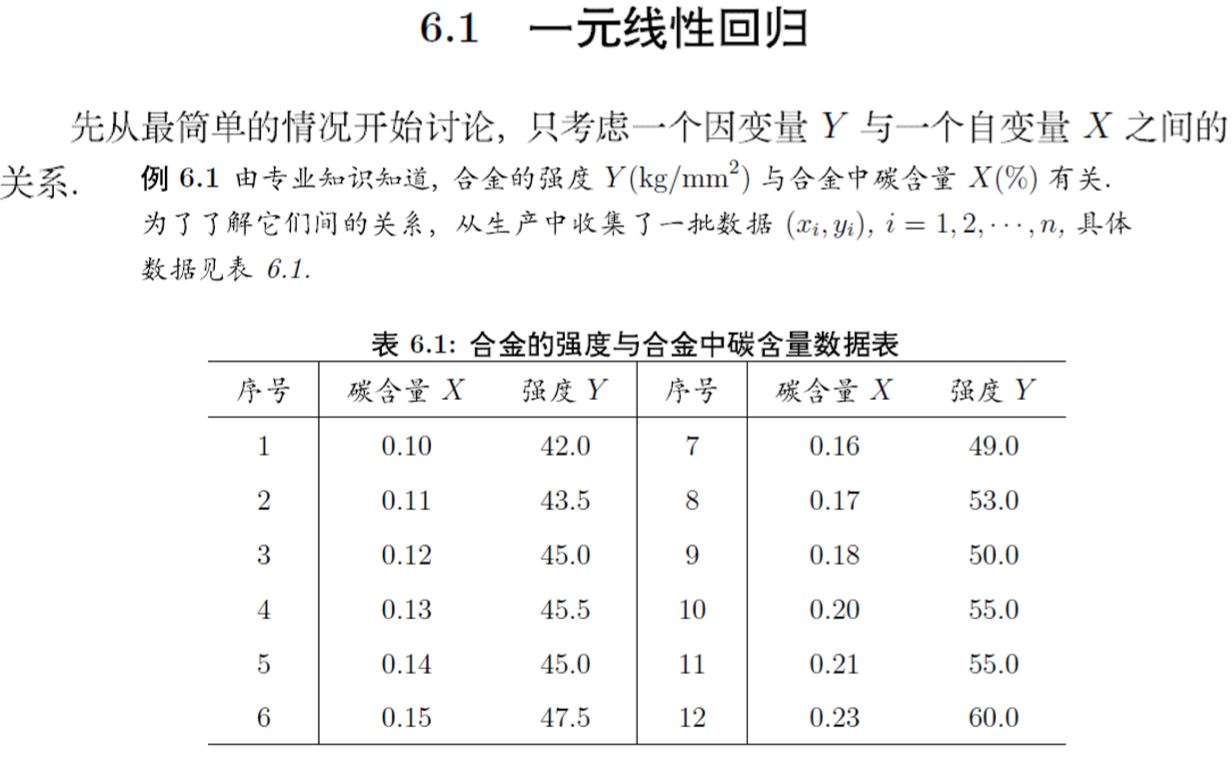
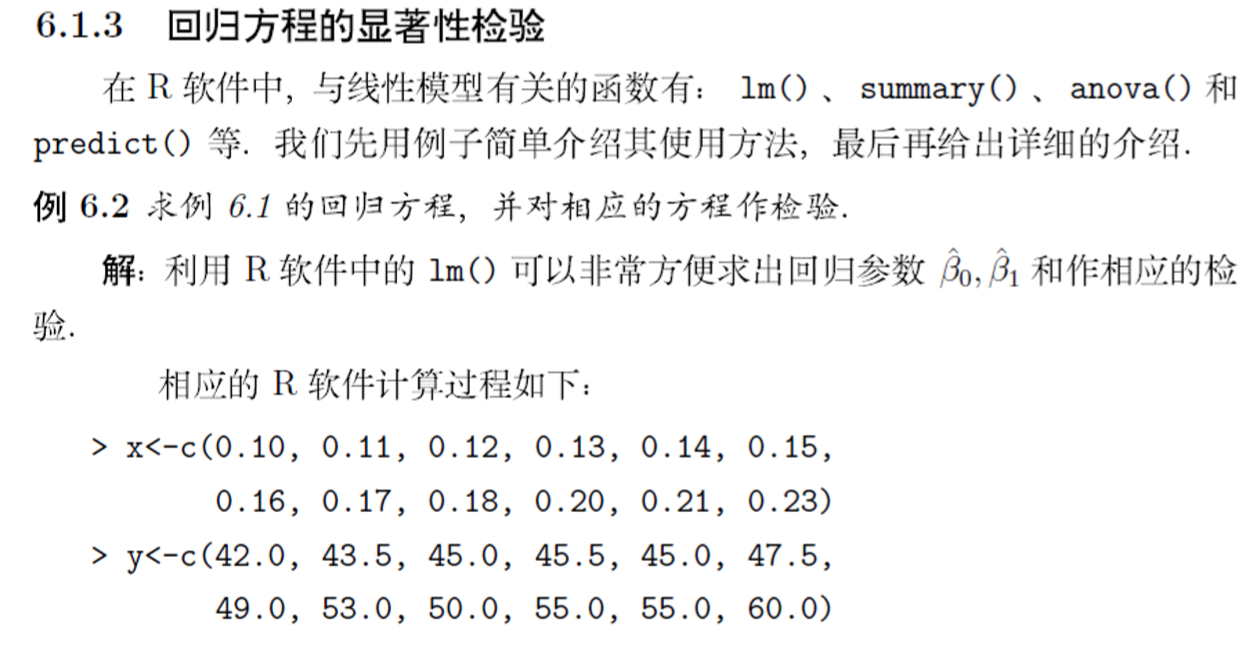
> x<-c(0.10,0.11,0.12,0.13,0.14,0.15,0.16,0.17,0.18,0.20,0.21,0.23)
> y<-c(42.0,43.5,45.0,45.5,45.0,47.5,49.0,53.0,50.0,55.0,55.0,60.0)
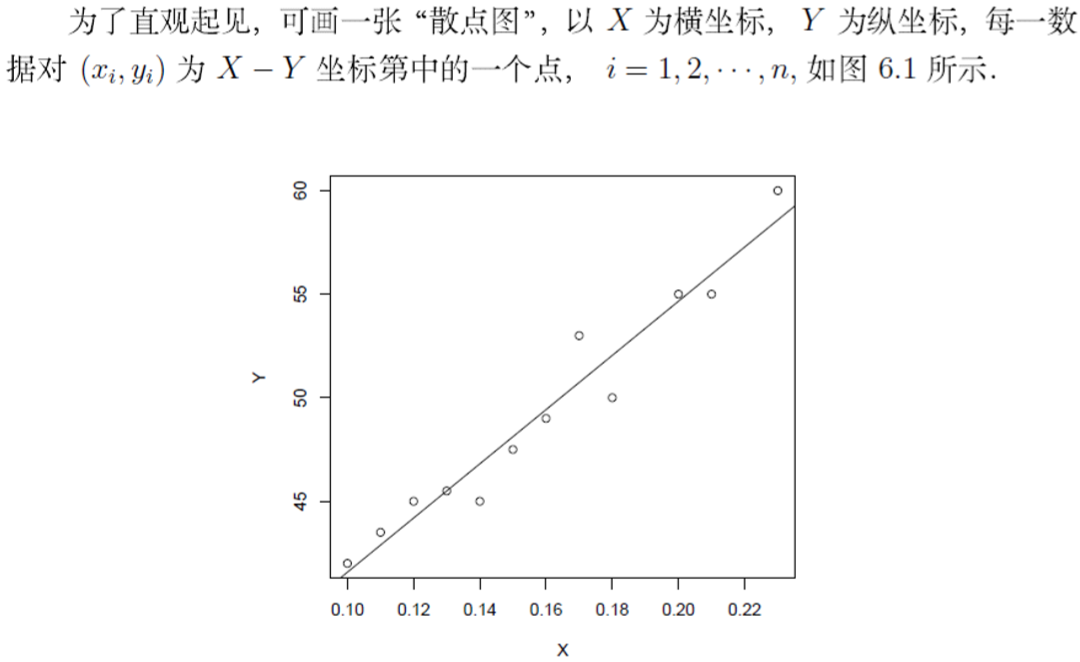
> plot(x~y)
> lm.sol<-lm(y ~ x)
> summary(lm.sol)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-2.0431 -0.7056 0.1694 0.6633 2.2653
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 28.493 1.580 18.04 5.88e-09 ***
x 130.835 9.683 13.51 9.50e-08 *** #所以y=130.835x+28.493,***表示显著性水平,*越多越好
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 #显著性水平
Residual standard error: 1.319 on 10 degrees of freedom
Multiple R-squared: 0.9481, Adjusted R-squared: 0.9429
F-statistic: 182.6 on 1 and 10 DF, p-value: 9.505e-08 ¥F检验,检验所有系数全是0的假设
> new=data.frame(x=0.16)#怎么预测多个数值的结果?
> lm.pred=predict(lm.sol,new,interval='prediction',level=0.95)
> lm.pred
fit lwr upr
1 49.42639 46.36621 52.48657


先求对数,再*100
> X<-matrix(c(
+ 194.5, 20.79, 1.3179, 131.79,
+ 194.3, 20.79, 1.3179, 131.79,
+ 197.9, 22.40, 1.3502, 135.02,
+ 198.4, 22.67, 1.3555, 135.55,
+ 199.4, 23.15, 1.3646, 136.46,
+ 199.9, 23.35, 1.3683, 136.83,
+ 200.9, 23.89, 1.3782, 137.82,
+ 201.1, 23.99, 1.3800, 138.00,
+ 201.4, 24.02, 1.3806, 138.06,
+ 201.3, 24.01, 1.3805, 138.05,
+ 203.6, 25.14, 1.4004, 140.04,
+ 204.6, 26.57, 1.4244, 142.44,
+ 209.5, 28.49, 1.4547, 145.47,
+ 208.6, 27.76, 1.4434, 144.34,
+ 210.7, 29.04, 1.4630, 146.30,
+ 211.9, 29.88, 1.4754, 147.54,
+ 212.2, 30.06, 1.4780, 147.80),
+ ncol=4, byrow=T,
+ dimnames = list(1:17, c("F", "h", "log", "log100")))#如何改变行和列的名称,如何按列排列数据?
>
> forbes<-data.frame(X)#把矩阵X转化为数据框
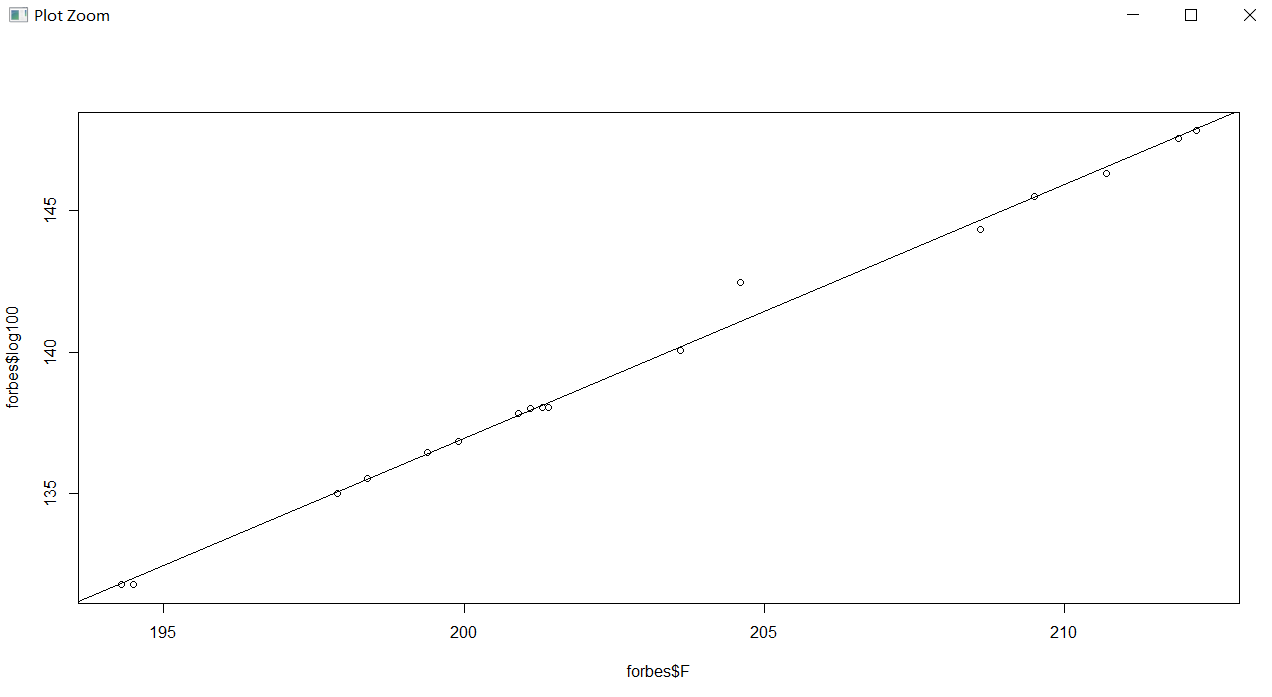
> plot(forbes$F, forbes$log100)#画出两个变量之间的散点图,观察是否存在线性趋势;学习
> #如何从数据框里面调取向量。怎么写坐标轴的名字和标题?
> #如何从数据框里面调取向量。怎么写坐标轴的名字和标题?
> lm.sol<-lm(log100~F, data=forbes)
> summary(lm.sol)
Call:
lm(formula = log100 ~ F, data = forbes)
Residuals:
Min 1Q Median 3Q Max
-0.32261 -0.14530 -0.06750 0.02111 1.35924
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -42.13087 3.33895 -12.62 2.17e-09 ***
F 0.89546 0.01645 54.45 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3789 on 15 degrees of freedom
Multiple R-squared: 0.995, Adjusted R-squared: 0.9946
F-statistic: 2965 on 1 and 15 DF, p-value: < 2.2e-16
> abline(lm.sol)#在散点图上添加直线
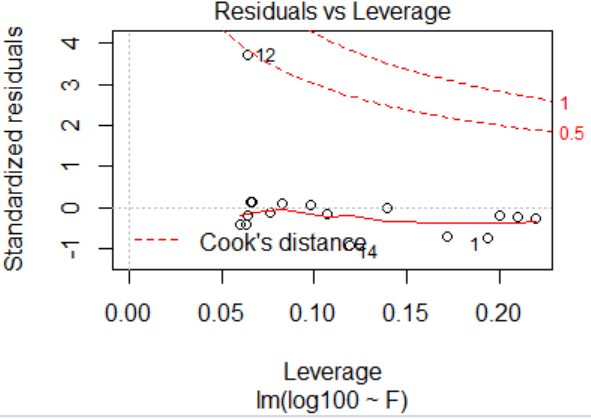
#残差检验 y.res<-residuals(lm.sol);plot(y.res)#画出残差图 text(12,y.res[12], labels=12,adj=1.2)
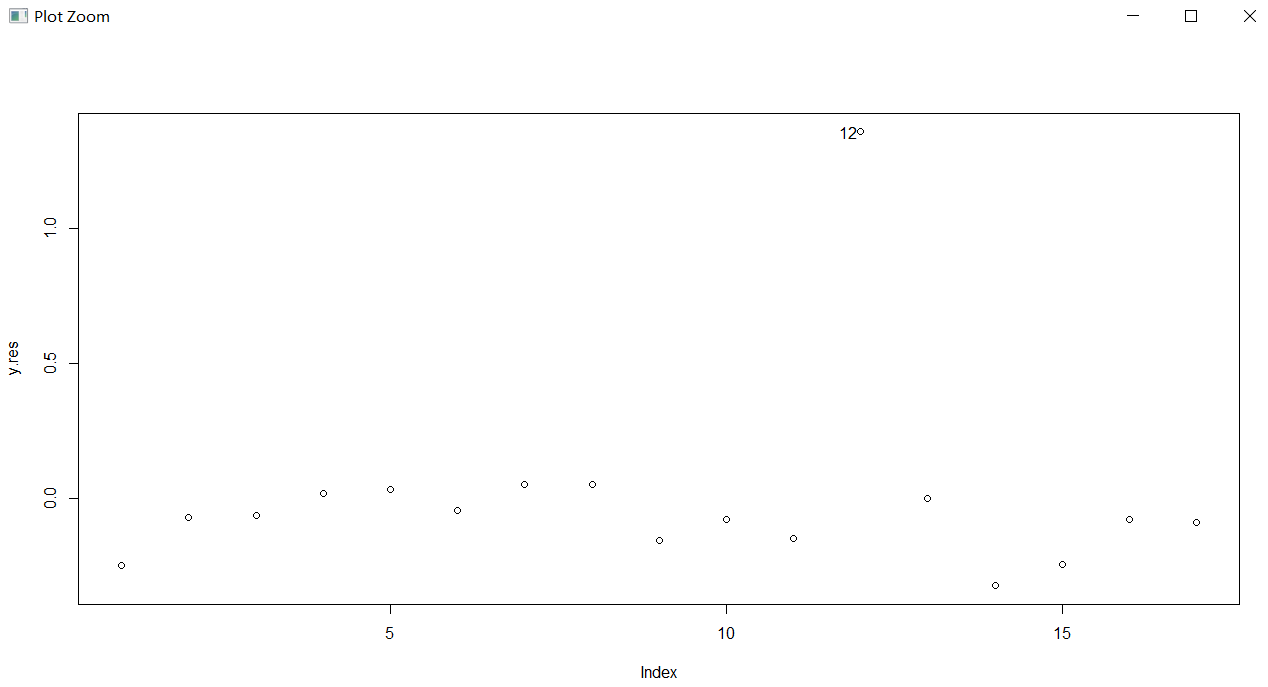
#异常值的判断 library(car) outlierTest(lm.sol)
> outlierTest(lm.sol) rstudent unadjusted p-value Bonferroni p 12 12.40369 6.1097e-09 1.0386e-07
> plot(lm.sol) Hit <Return> to see next plot: return Hit <Return> to see next plot: return Hit <Return> to see next plot: return Hit <Return> to see next plot: return
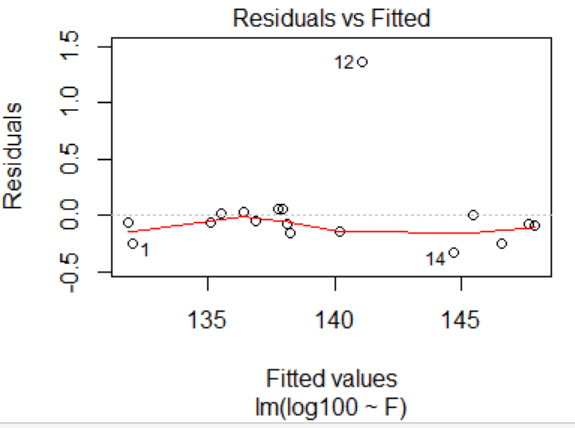
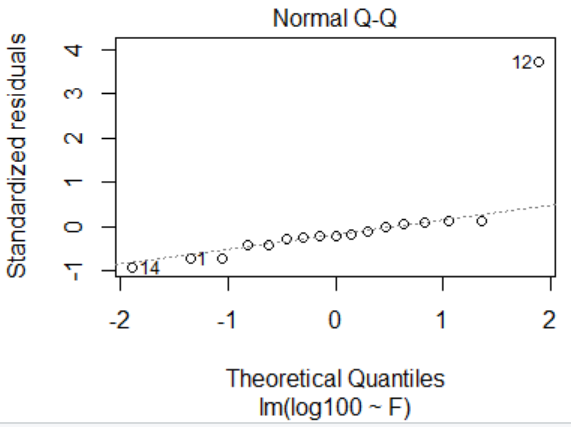
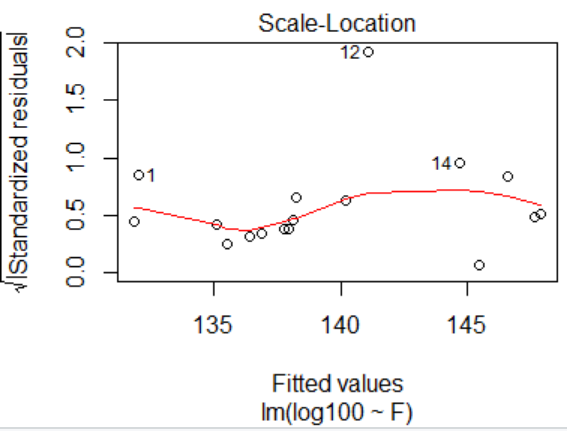
##################################6.6多元回归分析
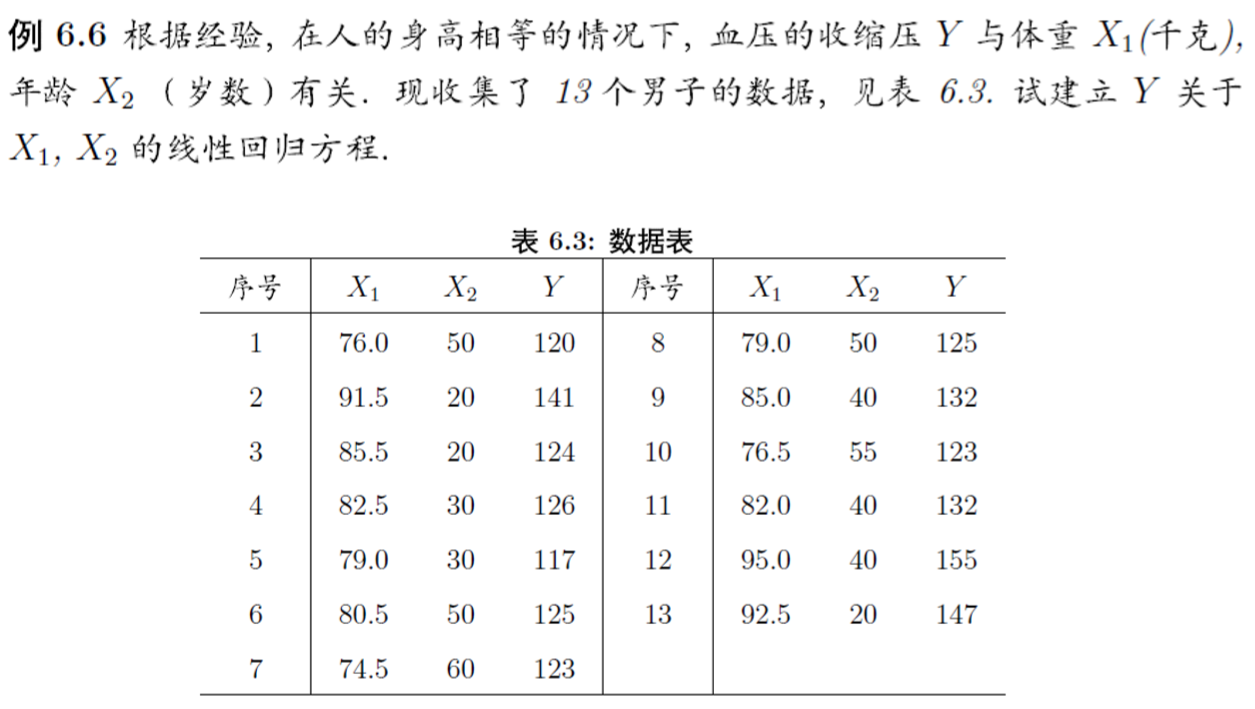
blood<-data.frame(
X1=c(76.0, 91.5, 85.5, 82.5, 79.0, 80.5, 74.5,
79.0, 85.0, 76.5, 82.0, 95.0, 92.5),
X2=c(50, 20, 20, 30, 30, 50, 60, 50, 40, 55,
40, 40, 20),
Y= c(120, 141, 124, 126, 117, 125, 123, 125,
132, 123, 132, 155, 147)
)
#多元回归分析时,最好先检查变量之间的相关性
cor(blood)
library(car)
scatterplotMatrix(blood,spread=F,lty.smooth=2,main='blood plot matrix')
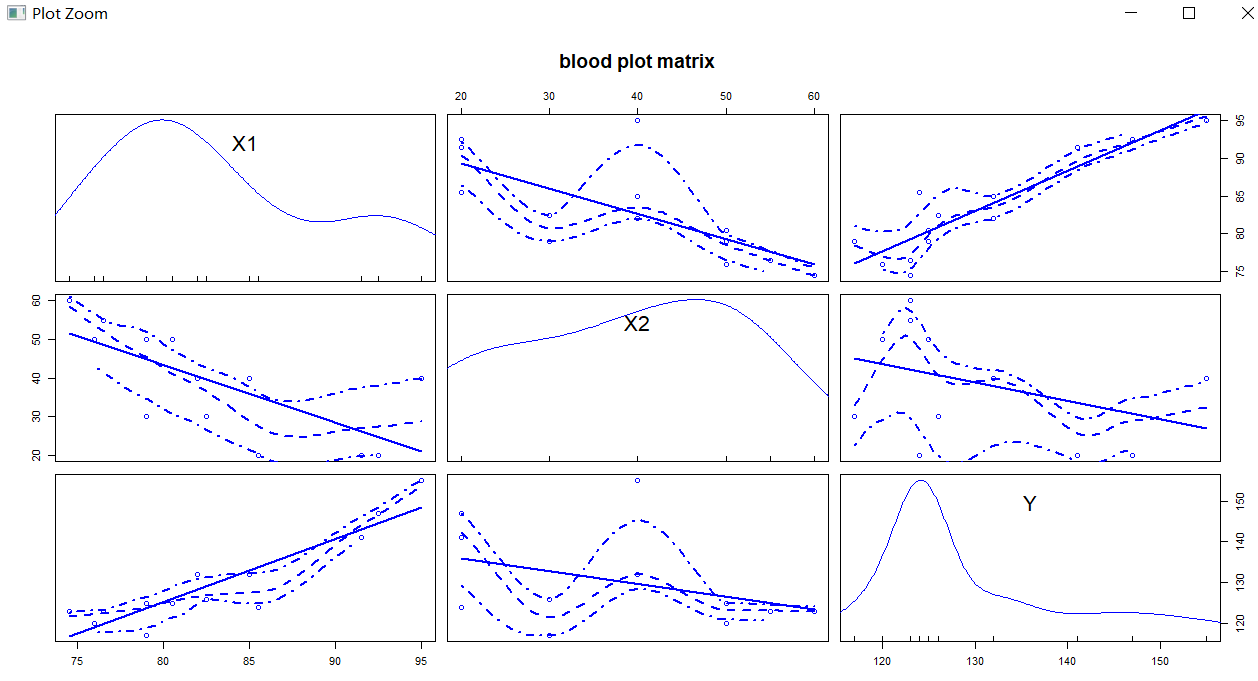
> lm.sol<-lm(Y ~ X1+X2, data=blood)
> summary(lm.sol)
Call:
lm(formula = Y ~ X1 + X2, data = blood)
Residuals:
Min 1Q Median 3Q Max
-4.0404 -1.0183 0.4640 0.6908 4.3274
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -62.96336 16.99976 -3.704 0.004083 **
X1 2.13656 0.17534 12.185 2.53e-07 ***
X2 0.40022 0.08321 4.810 0.000713 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.854 on 10 degrees of freedom
Multiple R-squared: 0.9461, Adjusted R-squared: 0.9354
F-statistic: 87.84 on 2 and 10 DF, p-value: 4.531e-07
> #回归系数的区间估计
> confint(lm.sol)
2.5 % 97.5 %
(Intercept) -100.8411862 -25.0855320
X1 1.7458709 2.5272454
X2 0.2148077 0.5856246
> #6.8预测
> new=data.frame(X1=80,X2=40)#怎么做多组预测?
> lm.pred=predict(lm.sol,new,interval='prediction',level=0.95)
> lm.pred
fit lwr upr
1 123.9699 117.2889 130.6509
所有代码:

#############6.2一元线性回归分析 x<-c(0.10,0.11,0.12,0.13,0.14,0.15,0.16,0.17,0.18,0.20,0.21,0.23) y<-c(42.0,43.5,45.0,45.5,45.0,47.5,49.0,53.0,50.0,55.0,55.0,60.0) plot(x~y) lm.sol<-lm(y ~ x) summary(lm.sol) #6.4做预测 new=data.frame(x=0.16)#怎么预测多个数值的结果? lm.pred=predict(lm.sol,new,interval='prediction',level=0.95) lm.pred ###### X<-matrix(c( 194.5, 20.79, 1.3179, 131.79, 194.3, 20.79, 1.3179, 131.79, 197.9, 22.40, 1.3502, 135.02, 198.4, 22.67, 1.3555, 135.55, 199.4, 23.15, 1.3646, 136.46, 199.9, 23.35, 1.3683, 136.83, 200.9, 23.89, 1.3782, 137.82, 201.1, 23.99, 1.3800, 138.00, 201.4, 24.02, 1.3806, 138.06, 201.3, 24.01, 1.3805, 138.05, 203.6, 25.14, 1.4004, 140.04, 204.6, 26.57, 1.4244, 142.44, 209.5, 28.49, 1.4547, 145.47, 208.6, 27.76, 1.4434, 144.34, 210.7, 29.04, 1.4630, 146.30, 211.9, 29.88, 1.4754, 147.54, 212.2, 30.06, 1.4780, 147.80), ncol=4, byrow=T, dimnames = list(1:17, c("F", "h", "log", "log100")))#如何改变行和列的名称,如何按列排列数据? forbes<-data.frame(X)#把矩阵X转化为数据框 plot(forbes$F, forbes$log100)#画出两个变量之间的散点图,观察是否存在线性趋势;学习 #如何从数据框里面调取向量。怎么写坐标轴的名字和标题? lm.sol<-lm(log100~F, data=forbes) summary(lm.sol) abline(lm.sol)#在散点图上添加直线 #残差检验 y.res<-residuals(lm.sol);plot(y.res)#画出残差图 text(12,y.res[12], labels=12,adj=1.2) #异常值的判断 library(car) outlierTest(lm.sol) #去除异常值 i<-1:17; forbes12<-data.frame(X[i!=12, ]) lm12<-lm(log100~F, data=forbes12) summary(lm12) ##################################6.6多元回归分析 blood<-data.frame( X1=c(76.0, 91.5, 85.5, 82.5, 79.0, 80.5, 74.5, 79.0, 85.0, 76.5, 82.0, 95.0, 92.5), X2=c(50, 20, 20, 30, 30, 50, 60, 50, 40, 55, 40, 40, 20), Y= c(120, 141, 124, 126, 117, 125, 123, 125, 132, 123, 132, 155, 147) ) #多元回归分析时,最好先检查变量之间的相关性 cor(blood) library(car) scatterplotMatrix(blood,spread=F,lty.smooth=2,main='blood plot matrix') lm.sol<-lm(Y ~ X1+X2, data=blood) summary(lm.sol) #回归系数的区间估计 confint(lm.sol) #6.8预测 new=data.frame(X1=80,X2=40)#怎么做多组预测? lm.pred=predict(lm.sol,new,interval='prediction',level=0.95) lm.pred
