麦克找了个新女朋友,玛丽卡对他非常恼火并伺机报复。
因为她和他们不住在同一个城市,因此她开始准备她的长途旅行。
在这个国家中每两个城市之间最多只有一条路相通,并且我们知道从一个城市到另一个城市路上所需花费的时间。
麦克在车中无意中听到有一条路正在维修,并且那儿正堵车,但没听清楚到底是哪一条路。无论哪一条路正在维修,从玛丽卡所在的城市都能到达麦克所在的城市。
玛丽卡将只从不堵车的路上通过,并且她将按最短路线行车。麦克希望知道在最糟糕的情况下玛丽卡到达他所在的城市需要多长时间,这样他就能保证他的女朋友离开该城市足够远。
编写程序,帮助麦克找出玛丽卡按最短路线通过不堵车道路到达他所在城市所需的最长时间(用分钟表示)。
第一行有两个用空格隔开的数N和M,分别表示城市的数量以及城市间道路的数量。1≤N≤1000,1≤M≤N*(N-1)/2。城市用数字1至N标识,麦克在城市1中,玛丽卡在城市N中。
接下来的M行中每行包含三个用空格隔开的数A,B和V。其中1≤A,B≤N,1≤V≤1000。这些数字表示在A和城市B中间有一条双行道,并且在V分钟内是就能通过。
输出文件的第一行中写出用分钟表示的最长时间,在这段时间中,无论哪条路在堵车,玛丽卡应该能够到达麦克处,如果少于这个时间的话,则必定存在一条路,该条路一旦堵车,玛丽卡就不能够赶到麦克处。
5 7
1 2 8
1 4 10
2 3 9
2 4 10
2 5 1
3 4 7
3 5 10
27
这道题乍一看是个单源最短路,只有1000的数据几乎是想咋做就咋做。
但再仔细一看输出描述,才发现要处理堵车的情况,想出来的解法很暴力,先SPFA一遍并记录路径,再依次删掉路径中的每条边再SPFA,取最大值。
那么如何记录路径呢?
我的方法是用一个pre数组来记录到当前节点的最优点/边。
1,pre[i]表示从1到i的最短路上的上一个节点,如图:
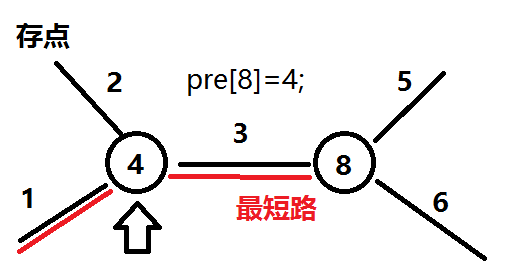
pre[i]表示1到点i的最短路的前一个点的编号,只需不停地x=pre[x]再找到对应的边删除即可。
2,pre[i]表示从1到i的最短路上一条边的编号,如图:
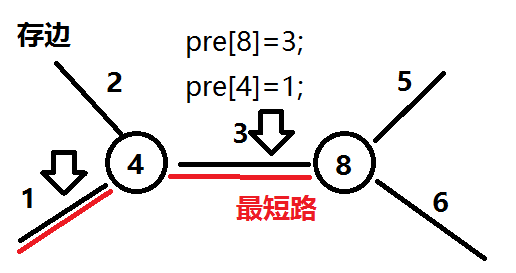
pre[i]表示到1点i的最短路的前一条边的编号,int edge=pre[x];再循环edge=pre[e[edge].u];只需将编号为edge的边删除。
本题是无向边,需要再删除另一个方向上的边,但在邻接表存边时一条无向边被拆为两条有向边,且编号相邻,所以找到一条边时再删去+1或-1的边。
在SPFA的过程中,每当松弛一条边时边更新pre数组,即可记录下路径。
代码如下,使用pre数组记录边的编号。
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 #define inf 100000000 6 int d[1001],q[100001],head[1001],pre[1001],n,m,cnt,h,t,ans; 7 bool vis[10001]; 8 struct edge 9 { 10 int u,v,val,next; 11 bool no;//是否堵车 12 }e[5000050]; 13 void spfa(bool re)//re为true则记录路径 14 { 15 h=t=1; 16 q[t++]=1; 17 while(h<t) 18 { 19 for(int i=head[q[h]];i!=0;i=e[i].next) 20 { 21 if(e[i].no)continue; 22 if(d[q[h]]+e[i].val<d[e[i].v]) 23 { 24 d[e[i].v]=d[q[h]]+e[i].val; 25 if(re)pre[e[i].v]=i;//记录边的编号i 26 if(!vis[e[i].v]) 27 { 28 q[t++]=e[i].v; 29 vis[e[i].v]=true; 30 } 31 } 32 } 33 vis[q[h]]=false; 34 ++h; 35 } 36 } 37 void add(int uu,int vv,int ww)//一条无向边被拆为二条有向边储存,编号分别为cnt,cnt+1 38 { 39 e[++cnt].next=head[uu]; 40 head[uu]=cnt; 41 e[cnt].u=uu; 42 e[cnt].v=vv; 43 e[cnt].val=ww; 44 e[++cnt].next=head[vv]; 45 head[vv]=cnt; 46 e[cnt].u=vv; 47 e[cnt].v=uu; 48 e[cnt].val=ww; 49 } 50 int main() 51 { 52 int x,y,w,now; 53 scanf("%d%d",&n,&m); 54 for(int i=2;i<=n;i++) 55 d[i]=inf; 56 for(int i=1;i<=m;i++) 57 { 58 scanf("%d%d%d",&x,&y,&w); 59 add(x,y,w); 60 } 61 spfa(true); 62 ans=d[n]; 63 now=pre[n]; 64 while(1) 65 { 66 if(now+1<=cnt&&e[now+1].u==e[now].v&&e[now+1].v==e[now].u)//找到另一条应删去的边 67 { 68 e[now+1].no=e[now].no=true; 69 memset(vis,false,sizeof(vis)); 70 for(int i=2;i<=n;i++)d[i]=inf; 71 spfa(false); 72 e[now+1].no=e[now].no=false; 73 ans=max(ans,d[n]); 74 } 75 else if(now-1>=1&&e[now-1].u==e[now].v&&e[now-1].v==e[now].u) 76 { 77 e[now-1].no=e[now].no=true; 78 memset(vis,false,sizeof(vis)); 79 for(int i=2;i<=n;i++)d[i]=inf; 80 spfa(false); 81 e[now-1].no=e[now].no=false; 82 ans=max(ans,d[n]); 83 } 84 if(e[now].u==1)break;//若边的起点为1,则退出 85 now=pre[e[now].u];//下一条边 86 } 87 printf("%d",ans); 88 return 0; 89 }