题目描述
对Samuel星球的探险已经取得了非常巨大的成就,于是科学家们将目光投向了Samuel星球所在的星系——一个巨大的由千百万星球构成的Samuel星系。
星际空间站的Samuel II巨型计算机经过长期探测,已经锁定了Samuel星系中许多星球的空间坐标,并对这些星球从1开始编号1、2、3……。
一些先遣飞船已经出发,在星球之间开辟探险航线。
探险航线是双向的,例如从1号星球到3号星球开辟探险航线,那么从3号星球到1号星球也可以使用这条航线。
例如下图所示:
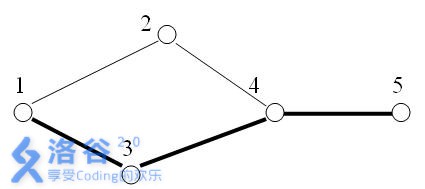
在5个星球之间,有5条探险航线。
A、B两星球之间,如果某条航线不存在,就无法从A星球抵达B星球,我们则称这条航线为关键航线。
显然上图中,1号与5号星球之间的关键航线有1条:即为4-5航线。
然而,在宇宙中一些未知的磁暴和行星的冲撞,使得已有的某些航线被破坏,随着越来越多的航线被破坏,探险飞船又不能及时回复这些航线,可见两个星球之间的关键航线会越来越多。
假设在上图中,航线4-2(从4号星球到2号星球)被破坏。此时,1号与5号星球之间的关键航线就有3条:1-3,3-4,4-5。
小联的任务是,不断关注航线被破坏的情况,并随时给出两个星球之间的关键航线数目。现在请你帮助完成。
输入输出格式
输入格式:
第一行有两个整数N,M。表示有N个星球(1< N < 30000),初始时已经有M条航线(1 < M < 100000)。随后有M行,每行有两个不相同的整数A、B表示在星球A与B之间存在一条航线。接下来每行有三个整数C、A、B。C为1表示询问当前星球A和星球B之间有多少条关键航线;C为0表示在星球A和星球B之间的航线被破坏,当后面再遇到C为1的情况时,表示询问航线被破坏后,关键路径的情况,且航线破坏后不可恢复; C为-1表示输入文件结束,这时该行没有A,B的值。被破坏的航线数目与询问的次数总和不超过40000。
输出格式:
对每个C为1的询问,输出一行一个整数表示关键航线数目。
输入输出样例
说明
我们保证无论航线如何被破坏,任意时刻任意两个星球都能够相互到达。在整个数据中,任意两个星球之间最多只可能存在一条直接的航线。
题解
LCT维护双联通分量
然而蒟蒻完全不知道怎么实现orz,于是只好(恬不知耻地)看着题解学了一个晚上
首先肯定是要将所有操作读入倒叙做的
还有,答案就是缩完点后两点间的路径长
最重要的问题是怎么连边
如果本来不相连,直接连
已经在同一个双连通分量,忽略
否则的话,用并查集维护在哪一个双连通,直接暴力将所有缩到一起就是了
可以发现每缩一次点就减少一个,所以最多缩$n$次
还有一个细节,我好久才搞明白,写在代码里了
1 //minamoto 2 #include<bits/stdc++.h> 3 using namespace std; 4 #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) 5 char buf[1<<21],*p1=buf,*p2=buf; 6 inline int read(){ 7 #define num ch-'0' 8 char ch;bool flag=0;int res; 9 while(!isdigit(ch=getc())) 10 (ch=='-')&&(flag=true); 11 for(res=num;isdigit(ch=getc());res=res*10+num); 12 (flag)&&(res=-res); 13 #undef num 14 return res; 15 } 16 char obuf[1<<24],*o=obuf; 17 inline void print(int x){ 18 if(x>9) print(x/10); 19 *o++=x%10+48; 20 } 21 const int N=50005,M=100005; 22 struct edge{ 23 int x,y; 24 inline bool operator <(const edge&b)const 25 {return x<b.x||(x==b.x&&y<b.y);} 26 }e[M]; 27 int fa[N],f[N],sz[N],s[N],ch[N][2],rev[N],vis[N],top; 28 int ff(int x){return f[x]==x?x:f[x]=ff(f[x]);} 29 inline bool isroot(int x){return ch[fa[x]][0]!=x&&ch[fa[x]][1]!=x;} 30 inline void pushup(int x){sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+1;} 31 inline void pushdown(int x){ 32 if(x&&rev[x]){ 33 swap(ch[x][0],ch[x][1]); 34 rev[ch[x][0]]^=1,rev[ch[x][1]]^=1,rev[x]=0; 35 } 36 } 37 void rotate(int x){ 38 int y=fa[x],z=fa[y],d=ch[y][1]==x; 39 if(!isroot(y)) ch[z][ch[z][1]==y]=x; 40 fa[x]=z,fa[y]=x,fa[ch[x][d^1]]=y,ch[y][d]=ch[x][d^1],ch[x][d^1]=y;pushup(y); 41 } 42 void splay(int x){ 43 s[top=1]=x;for(int i=x;!isroot(i);i=fa[i]) s[++top]=fa[i]; 44 for(int i=top;i;--i) pushdown(s[i]); 45 for(int y=fa[x],z=fa[y];!isroot(x);y=fa[x],z=fa[y]){ 46 if(!isroot(y)) ((ch[y][1]==x)^(ch[z][1]==y))?rotate(x):rotate(y); 47 rotate(x); 48 } 49 pushup(x); 50 } 51 void access(int x){ 52 for(int y=0;x;y=x,x=fa[x]=ff(fa[x])) 53 splay(x),ch[x][1]=y,pushup(x); 54 } 55 inline void makeroot(int x){ 56 access(x),splay(x),rev[x]^=1; 57 } 58 int findroot(int x){ 59 access(x),splay(x); 60 pushdown(x); 61 while(ch[x][0]) pushdown(x=ch[x][0]); 62 splay(x); 63 return x; 64 } 65 inline void split(int x,int y){ 66 makeroot(x),access(y),splay(y); 67 } 68 void del(int x,int y){ 69 if(x) f[x]=y,del(ch[x][0],y),del(ch[x][1],y); 70 } 71 void merge(int x,int y){ 72 if(x==y) return; 73 makeroot(x); 74 if(findroot(y)!=x) return(void)(fa[x]=y); 75 /*makeroot的时候打了标记 76 所以findroot的时候顺便把标记放掉 77 再把根转到splay的根节点 78 然后因为x为根,y深度必然大于x 79 所以把所有右节点搞掉就好了 80 */ 81 del(ch[x][1],x); 82 ch[x][1]=0,pushup(x); 83 } 84 int op[N],ans[M],a[M],b[M]; 85 int main(){ 86 //freopen("testdata.in","r",stdin); 87 int n,m,i,j; 88 n=read(),m=read(); 89 for(i=1;i<=n;++i) sz[i]=1,f[i]=i; 90 for(i=1;i<=m;++i){ 91 int u=read(),v=read(); 92 if(u>v) swap(u,v); 93 e[i]=(edge){u,v}; 94 } 95 sort(e+1,e+1+m); 96 for(j=1;op[j]=read(),op[j]!=-1;++j){ 97 int u=read(),v=read(); 98 if(!op[j]){ 99 if(u>v) swap(u,v); 100 vis[lower_bound(e+1,e+1+m,(edge){u,v})-e]=1; 101 } 102 a[j]=u,b[j]=v; 103 } 104 for(i=1;i<=m;++i) 105 if(!vis[i]) merge(ff(e[i].x),ff(e[i].y)); 106 for(i=0,--j;j;--j){ 107 int u=ff(a[j]),v=ff(b[j]); 108 if(op[j]) split(u,v),ans[++i]=sz[v]-1; 109 else merge(u,v); 110 } 111 while(i) print(ans[i--]),*o++=' '; 112 fwrite(obuf,o-obuf,1,stdout); 113 return 0; 114 }