Welcome to Innopolis city. Throughout the whole year, Innopolis citizens suffer from everlasting city construction.
From the window in your room, you see the sequence of n hills, where i-th of them has height ai. The Innopolis administration wants to build some houses on the hills. However, for the sake of city appearance, a house can be only built on the hill, which is strictly higher than neighbouring hills (if they are present). For example, if the sequence of heights is 5, 4, 6, 2, then houses could be built on hills with heights 5 and 6 only.
The Innopolis administration has an excavator, that can decrease the height of an arbitrary hill by one in one hour. The excavator can only work on one hill at a time. It is allowed to decrease hills up to zero height, or even to negative values. Increasing height of any hill is impossible. The city administration wants to build k houses, so there must be at least k hills that satisfy the condition above. What is the minimum time required to adjust the hills to achieve the administration's plan?
However, the exact value of k is not yet determined, so could you please calculate answers for all k in range  ? Here
? Here 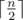 denotes n divided by two, rounded up.
denotes n divided by two, rounded up.
The first line of input contains the only integer n (1 ≤ n ≤ 5000)—the number of the hills in the sequence.
Second line contains n integers ai (1 ≤ ai ≤ 100 000)—the heights of the hills in the sequence.
Print exactly 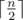 numbers separated by spaces. The i-th printed number should be equal to the minimum number of hours required to level hills so it becomes possible to build i houses.
numbers separated by spaces. The i-th printed number should be equal to the minimum number of hours required to level hills so it becomes possible to build i houses.
5
1 1 1 1 1
1 2 2
3
1 2 3
0 2
5
1 2 3 2 2
0 1 3
In the first example, to get at least one hill suitable for construction, one can decrease the second hill by one in one hour, then the sequence of heights becomes 1, 0, 1, 1, 1 and the first hill becomes suitable for construction.
In the first example, to get at least two or at least three suitable hills, one can decrease the second and the fourth hills, then the sequence of heights becomes 1, 0, 1, 0, 1, and hills 1, 3, 5 become suitable for construction.
链接:http://codeforces.com/contest/1012/problem/C
题目大意:
给定一段序列,如果其中一个点上数大于旁边的数就可以为特殊点,然后我们可以减少任一点上的数,减少其中任意一点的数每减少1时间就消耗1,求获得1...floor(n/2)个特殊点所耗费的时间。
f[i][j][0]表示选择在第i个点已经有j个特殊点,且第i个点不一定是特殊点
f[i][j][1]表示选择在第i个点已经有j个特殊点,且第i个点一定是特殊点
至于dp方程在代码中做注释
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int N=5005; int h[N],f[N][N>>1][2],ans[N]; int main() { int n; scanf("%d",&n); for(int i=1;i<=n;++i) scanf("%d",&h[i]); memset(f,0x3f,sizeof(f)); memset(ans,0x3f,sizeof(ans)); f[2][1][0]=f[1][1][1]=max(0,h[2]-h[1]+1); f[2][1][1]=max(0,h[1]-h[2]+1)+max(0,h[3]-h[2]+1); ans[1]=min(f[2][1][1],f[1][1][1]); for(int i=1;i<=n;++i) f[i][0][0]=0; for(int i=3;i<=n;++i) for(int j=1;j<=(i+1)>>1;++j) { f[i][j][0]=min(f[i-1][j][1],f[i-1][j][0]);//这一点不是可以考虑上一点的情况直接转移 f[i][j][1]=f[i-2][j-1][1]+max(0,max((h[i-2]>h[i-1]?h[i-1]:h[i-2]-1)-h[i]+1,0)); //如果这一点选择成为特殊点,它会受到前两个点和后一个点的影响,我们思考前一个的高度可能会改变就是为了让前面的i-2的点成为特殊点时会消减i-1的高度 f[i][j][1]=min(f[i][j][1],f[i-2][j-1][0]+max(h[i-1]-h[i]+1,0)); f[i][j][1]+=max(0,h[i+1]-h[i]+1); ans[j]=min(ans[j],min(f[i][j][0],f[i][j][1])); } for(int j=1;j<=(n+1)>>1;++j) printf("%d ",ans[j]); return 0; }