显然,这是一道 DP 题。
于是设 f[i] 表示第 i 分钟发出一辆车所要的最小时间,设 t为最后一个人到达车站的时间。
得到状态转移方程: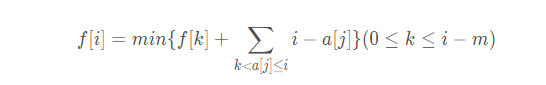
其中 k 表示上一辆末班车发车的时间。
那么最后的答案即为:ans=min{f[i]}(t≤i<t+m)
i<t+m 是因为最后一个人等的时间不会超过 m 分钟,不然他可以直接乘之前的一辆走,肯定不是最优解。
时间复杂度: Θ(t2n)
优化
1、前缀和优化
令 cnt[i] 表示到 i 止到达车站的人数和
sum[i]表示到 i为止到达车站的人的时间总和
显然有: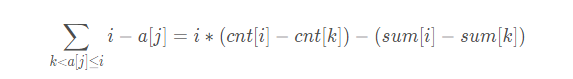
即,总等待时间 = i×(i∼k内总人数) − 等待时间在 i∼k 内所有人的等待时间之和。
附上一张图帮助理解:
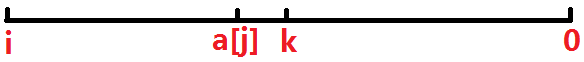
于是方程变为: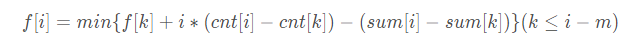
时间复杂度:Θ(t2)
2、转移优化
显然,没有一位同学的等待时间会超过 2m 分钟。
简单证明:
考虑最坏的情况,在 k 时刻发了一辆车,有个同学在 k+1 时到达车站,那么摆渡车将在 k+m 时返回,考虑到等待其它学生的情况,摆渡车最晚会在 k+2m−1时发车,否则还不如分别在 k+m 和 k+2m 的时候发出。
所以, k 的范围就变为: i−2m<k≤i−m。
时间复杂度: Θ(tm)
#include<bits/stdc++.h> #define ll long long #define me(x) memset(x,0,sizeof(x)) #define bi(x) memset(x,0x3f,sizeof(x)) #define ud using namespace std ud; const int maxn=1e7+10; int last_time=-9876543,ans=1<<30; int N,M,t[maxn],f[maxn],sum[maxn]={},cnt[maxn]={}; int main() { scanf("%d",&N); scanf("%d",&M); for(int i=1;i<=N;++i) { scanf("%d",&t[i]); // Find the last person who reach the station last_time=max(last_time,t[i]); ++cnt[t[i]];//从0到i时间为止到达车站的人数和 sum[t[i]]+=t[i];//从0到i时间为止到达车站的人的时间总和 } for(int i=1;i<last_time+M;++i) { cnt[i]+=cnt[i-1]; sum[i]+=sum[i-1]; } for(int i=0;i<last_time+M;++i) { if(i>=M&&cnt[i-M]==cnt[i]) { f[i]=f[i-M]; continue; } f[i]=cnt[i]*i-sum[i]; for(int j=max(i-(M<<1)+1,0);j<=i-M;++j) f[i]=min(f[i],f[j]+(cnt[i]-cnt[j])*i-(sum[i]-sum[j])); } for(int i=last_time;i<last_time+M;++i) ans=min(ans,f[i]); printf("%d ",ans); return 0; }