题目描述
有 nn 个同学(编号为 11 到 nn )正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象,其中,编号为 ii 的同学的信息传递对象是编号为 T_iTi 的同学。
游戏开始时,每人都只知道自己的生日。之后每一轮中,所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象(注意:可能有人可以从若干人那里获取信息, 但是每人只会把信息告诉一个人,即自己的信息传递对象)。当有人从别人口中得知自 己的生日时,游戏结束。请问该游戏一共可以进行几轮?
输入输出格式
输入格式:
共22行。
第11行包含1个正整数 nn ,表示 nn 个人。
第22行包含 nn 个用空格隔开的正整数 T_1,T_2,cdotscdots,T_nT1,T2,⋯⋯,Tn ,其中第 ii 个整数 T_iTi 表示编号为 ii 的同学的信息传递对象是编号为 T_iTi 的同学, T_i leq nTi≤n 且 T_i eq iTi≠i 。
输出格式:
11个整数,表示游戏一共可以进行多少轮。
输入输出样例
说明
样例1解释
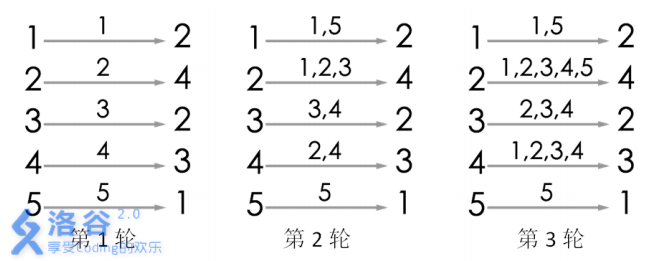
游戏的流程如图所示。当进行完第33 轮游戏后, 44号玩家会听到 22 号玩家告诉他自己的生日,所以答案为 33。当然,第 33 轮游戏后,22号玩家、 33 号玩家都能从自己的消息来源得知自己的生日,同样符合游戏结束的条件。
对于 30\%30%的数据, n ≤ 200n≤200;
对于 60\%60%的数据, n ≤ 2500n≤2500;
对于100\%100%的数据, n ≤ 200000n≤200000。
拓扑排序可以求是否有环 但是我不会求最小环
dfs 200000肯定会超时
可以采用拓扑排序优化 +dfs
300ms蒟蒻代码:

#include<bits/stdc++.h> using namespace std; //input b y bxd #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define RI(n) scanf("%d",&(n)) #define RII(n,m) scanf("%d%d",&n,&m) #define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k) #define RS(s) scanf("%s",s); #define ll long long #define REP(i,N) for(int i=0;i<(N);i++) #define CLR(A,v) memset(A,v,sizeof A) #define inf 0x3f3f3f3f ////////////////////////////////// #define N 200000+9 int in[N]; vector<int>edge[N]; int vis[N]; int minn; void dfs(int x,int cnt,int flag) { vis[x]=1; int k=edge[x][0]; vis[k]=1; if(k==flag) { minn=min(minn,cnt); return ; } dfs(k,cnt+1,flag); } int main() { int n; RI(n); rep(i,1,n) { int a,b; RI(a); in[a]++; edge[i].push_back(a); } queue<int>q; rep(i,1,n) if(!in[i])q.push(i);//后来还要取出来 所以这里cnt不用变 int cnt=0;//计算入读为0的点 while(!q.empty()) { int u=q.front();q.pop(); vis[u]=1;//去掉不成环的点 cnt++; if(edge[u].size()) rep(i,0,edge[u].size()-1) { int v=edge[u][i]; in[v]--; if(in[v]==0)q.push(v); } } minn=inf; rep(i,1,n) if(!vis[i]) dfs(i,1,i); cout<<minn; return 0; }
70ms
不要开队列!!!太慢了 只是借用拓扑排序的思想就够了

#include<bits/stdc++.h> using namespace std; //input b y bxd #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define RI(n) scanf("%d",&(n)) #define RII(n,m) scanf("%d%d",&n,&m) #define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k) #define RS(s) scanf("%s",s); #define ll long long #define REP(i,N) for(int i=0;i<(N);i++) #define CLR(A,v) memset(A,v,sizeof A) #define inf 0x3f3f3f3f ////////////////////////////////// #define N 200000+9 int in[N]; int edge[N]; int vis[N]; int minn; void dfs(int x,int cnt,int flag) { vis[x]=1; int k=edge[x]; if(k==flag) { minn=min(minn,cnt); return ; } dfs(k,cnt+1,flag); } void del(int x) { vis[x]=1; if( --in[edge[x]]==0 ) del(edge[x]); } int main() { int n; RI(n); rep(i,1,n) { int a,b; RI(a); in[a]++; edge[i]=a; } rep(i,1,n) if(!in[i]&&!vis[i]) del(i); minn=inf; rep(i,1,n) if(!vis[i]) dfs(i,1,i); cout<<minn; return 0; }
并查集 70ms
和今天写的带权并查集
一个原理

#include<bits/stdc++.h> using namespace std; //input b y bxd #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define RI(n) scanf("%d",&(n)) #define RII(n,m) scanf("%d%d",&n,&m) #define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k) #define RS(s) scanf("%s",s); #define ll long long #define REP(i,N) for(int i=0;i<(N);i++) #define CLR(A,v) memset(A,v,sizeof A) #define inf 0x3f3f3f3f ////////////////////////////////// #define N 200000+9 int f[N]; int dis[N];//维护距离头的距离 int minn; int find1(int x) { if(x==f[x])return x; int k=find1(f[x]); dis[x]+=dis[f[x]];//这个只是回溯 传递 并不是改权值 return f[x]=k; } void union1(int a,int b) { int x=find1(a); int y=find1(b); if(x==y) minn=min(minn,dis[a]+dis[b]+1); else { f[x]=y; dis[a]=dis[b]+1;//这里为改权值 } } int main() { int n; RI(n); rep(i,1,n) f[i]=i,dis[i]=0; minn=inf; rep(i,1,n) { int a; RI(a); union1(i,a); } cout<<minn; }
