裸的树形DP
P2016 战略游戏
对于(u,v)这条边,吾们在树上进行DP;
可以分两种情况讨论:
- 对于指向儿子的u,它选择不放放哨的,此时这条边要被看见必须在v放置。
状态转移:dp[u][0]+=dp[v][1];
2.放哨的弟弟已经在u啦,但不知道把放哨的再放在v上是不是更优的。
状态转移:dp[u][1]+=min(dp[v][0],dp[v][1]);
对于每棵树更新一下,递归实现即可。(包括原树与子树)
情况2的不确定v如图:
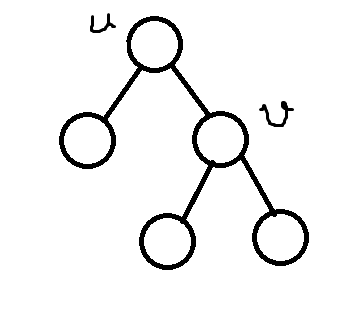
此时(如果以u为节点的话)最优解为(u,v);
这道题的代码实现:

1 #include<bits/stdc++.h>//动规 2 using namespace std; 3 struct edge{ 4 int nxt,to; 5 }ea[3010]; 6 int n,cnt,head[3010],dp[3010][2]; 7 void add_edge(int u,int v){ 8 ea[++cnt].to=v,ea[cnt].nxt=head[u],head[u]=cnt; 9 ea[++cnt].to=u,ea[cnt].nxt=head[v],head[v]=cnt; 10 } 11 void dfs(int u,int fa){ 12 dp[u][1]=1,dp[u][0]=0; 13 for(int i=head[u];i;i=ea[i].nxt){ 14 int v=ea[i].to; 15 if(v==fa) continue; 16 dfs(v,u); 17 dp[u][0]+=dp[v][1]; 18 dp[u][1]+=min(dp[v][0],dp[v][1]); 19 } 20 } 21 int main(){ 22 cin>>n; 23 for(int i=1,u,num;i<=n;i++){ 24 cin>>u>>num; 25 for(int i=1,v;i<=num;i++){ 26 cin>>v; 27 add_edge(u,v); 28 } 29 } 30 dfs(0,0); 31 cout<<min(dp[0][0],dp[0][1]); 32 }
P1122 最大紫薯和
这道题贪心很明显是对的,(因为局部最优解一定会影响到整体)但我是来说DP的……
设置状态dp[u]表示以u为根节点的子树的权值最大值。
递归更新的正确性同贪心思路。(如果此子树可删并且由叶子往根扫,不需要质疑它的正确性)
转移方程(话说跟数字三角形有异曲同工之妙)为:dp[u]=max(0,dp[v]);
同理分析,对于此图
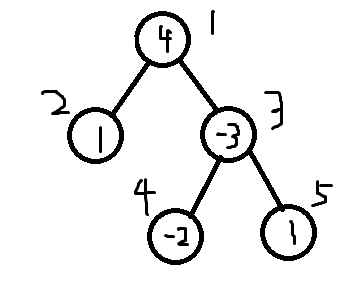
递归从叶子扫,把4号点删去,3,5点删去。
代码如下:

1 #include<bits/stdc++.h>//动规 2 using namespace std; 3 struct edge{ 4 int nxt,to; 5 }ea[35002]; 6 int n,cnt,head[35002],dp[35002],val[35002],ans=-2147483647; 7 void add_edge(int u,int v){ 8 ea[++cnt].to=v,ea[cnt].nxt=head[u],head[u]=cnt; 9 ea[++cnt].to=u,ea[cnt].nxt=head[v],head[v]=cnt; 10 } 11 void dfs(int u,int fa){ 12 dp[u]=val[u]; 13 for(int i=head[u];i;i=ea[i].nxt){ 14 int v=ea[i].to; 15 if(v==fa) continue; 16 dfs(v,u); 17 dp[u]+=max(0,dp[v]); 18 } 19 ans=max(ans,dp[u]); 20 } 21 int main(){ 22 cin>>n; 23 for(int i=1;i<=n;i++) cin>>val[i]; 24 for(int i=1,u,v;i<n;i++){ 25 cin>>u>>v; 26 add_edge(u,v); 27 } 28 dfs(1,0); 29 cout<<ans; 30 }
