话说它是(简单?)博弈论的基础的说?
这道模板还是很好打的,只要把所有数异或起来,ans如果为0就是必败局面,否则是必胜局面。
知道这个结论就很好打出来了啦!!

1 #include<bits/stdc++.h> 2 using namespace std; 3 int main(){ 4 int T; 5 cin>>T; 6 while(T--){ 7 int n,ans=0; 8 cin>>n; 9 for(int i=1,digit;i<=n;i++){ 10 cin>>digit; 11 ans^=digit; 12 } 13 if(!ans) cout<<"No"; 14 else cout<<"Yes"; 15 cout<<endl; 16 } 17 }
但我知道这肯定不是关键?
ヾ(o・ω・)ノ
是——怎么证明的说!!!
首先我们要了解nim的本质。
Nim游戏是博弈论中最经典的模型(之一),它又有着十分简单的规则和无比优美的结论 (我知道)Nim游戏是组合游戏(Combinatorial Games)的一种,准确来说,属于“Impartial Combinatorial Games”(以下简称ICG)。
第二个问题随之而出:ICG -> 1.两人;.
2.交替移动;
3.任意操作与以前无强制关系(为了最有可能会改变)
4.最后无法移动为负。
通常的Nim游戏的定义是这样的:有若干堆石子,每堆石子的数量都是有限的,合法的移动是“选择一堆石子并拿走若干颗(不能不拿)”,如果轮到某个人时所有的石子堆都已经被拿空了,则判负(因为他此刻没有任何合法的移动)。
目的是任何一方会在最开始出现必胜策略的时候遵循必胜策略。
那么(๑>ڡ<)✿ 什么是必胜策略?
定义:P-position(Previous)与N-position(Next)局面与无法进行任何移动的局面(也就是terminal position),遵循:
- 初始定义无法进行任何移动的局面为P(即最后一步),这样可以很好理解P是上一步操作的必胜局面。对于这一步的属于先手必败。(可向外拓展)
- 可以移动到P的局面是N局面,遵循这个原则就可以保证先手必胜。
- 所有只能导致N局面的局面是N局面,即指你走的这一步会导致下一操作者必胜。
Nim游戏结论
(Bouton's Theorem)对于一个Nim游戏的局面(a1,a2,...,an),它是P-position当且仅当a1^a2^...^an=0,其中^表示异或(xor)运算。
(雾)完全没有道理的和异或运算扯上了关系。(基本上就是按照两种position的证明来的。)
Nim游戏证明
- 这个判断将所有terminal position判为P-position;(废话) 全是0,异或——;
- 根据此判断,判为N-position的局面一定可以通过合法移动移动到某个P-position.即
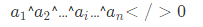
那么此时一定可以一步有
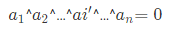 。
。
正确性:
3. 对于任意定义的P-position,一定不存在 一个合法移动移动到某个P-position。
正确性:因为异或求和满足消去律,那么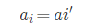 这不合法。
这不合法。
