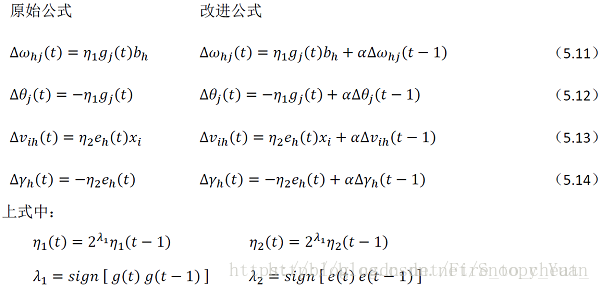试设计一个算法,能通过动态调整学习率显著提升收敛速度,编程实现该算法,并选择两个UCI数据集与标准的BP算法进行实验比较。
1.方法设计
传统的BP算法改进主要有两类:
- 启发式算法:如附加动量法,自适应算法
- 数值优化法:如共轭梯度法、牛顿迭代法、Levenberg-Marquardt算法
(1)附加动量项
这是一种广泛用于加速梯度下降法收敛的优化方法。其核心思想是:在梯度下降搜索时,若当前梯度下降与前一个梯度下降的方向相同,则加速搜索,反之则降速搜索。
标准BP算法的参数更新项为:
在添加动量项后,基于梯度下降的参数更新项为:
始终,为动量因子(取值 0~1)。上式也等价于:
式中 称为遗忘因子,表示上一次梯度下降的方向和大小信息对当前梯度下降的调整影响。
(2) 自适应学习率
附加动量法面临选取率的选取困难,进而产生收敛速度和收敛性的矛盾。于是另考虑引入学习速率自适应设计,这里给出一个·自适应设计方案:
上式中,为第t次迭代时的自适应学习速率因子,下面是一种计算实力:
其中为梯度方向:
这样,学习率的变化可以反映前面附加动量项中的“核心思想”。
(3)算法总结
将上述两种方法结合起来,形成动态自适应学习率的BP改进算法:

从上图及书中内容可知,输出层与隐层的梯度项不同,故而对应不同的学习率 η_1 和 η_2,算法的修改主要是第7行关于参数更新的内容:
将附加动量项与学习率自适应计算代入,得出公式(5.11-5.14)的调整如下图所示:
2.对比实验