《线性代数》知识点汇总

《线性代数》知识点汇总

原文网址：《线性代数》知识点汇总 - 知乎 (zhihu.com)

一、行列式：

行列式概念和性质

1、逆序数：所有的逆序的总数；

2、行列式定义：不同行不同列元素乘积代数和；

3、行列式性质：（用于化简行列式）；

（1）行列互换（转置），行列式的值不变；

（2）两行（列）互换，行列式变号；

（3）提公因式：行列式的某一行（列）的所有元素都乘以同一数 k，等于用数k乘此行列式；

（4）拆列分配：行列式中如果某一行（列）的元素都是两组数之和，那么这个行列式就等于两个行列式之和；

（5）一行（列）乘k加到另一行（列），行列式的值不变；

（6）两行成比例，行列式的值为0 ；

重要行列式

4、上（下）三角（主对角线）行列式的值等于主对角线元素的乘积；

5、副对角线行列式的值等于副对角线元素的乘积乘 $(-1)^{\frac{n\left( n-1 \right)}{2}}$ ；

6、Laplace展开式：（A是m阶矩阵，B是n阶矩阵），则

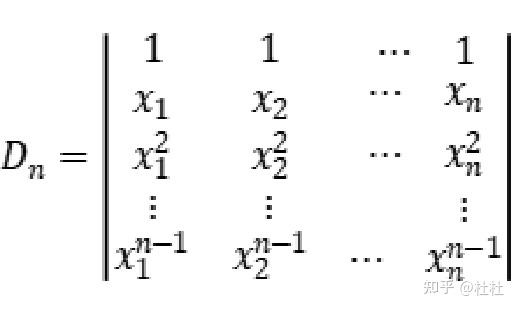
7、n阶（n≥2）范德蒙德行列式：

8、对角线的元素为a，其余元素为b的行列式的值：

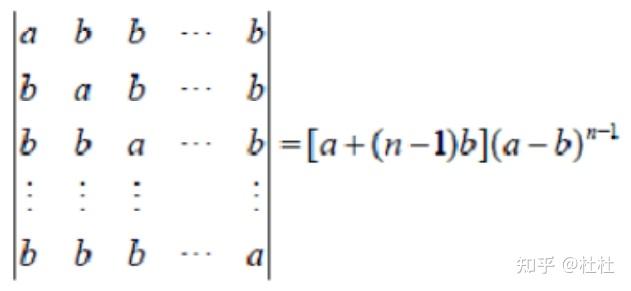
按行（列）展开

9、按行展开定理：

（1）任一行（列）的各元素与其对应的代数余子式乘积之和等于行列式的值；

（2）行列式中某一行（列）各个元素与另一行（列）对应元素的代数余子式乘积之和等于 0；

行列式公式

10、行列式七大公式：

（1） $|kA|=k n |A|$ ；

（2） $|AB|=|A| ·|B|$ ；

（3） $|A^{T} |=|A|$ ；

（4） $|A^{-1}|=|A|^{-1}$ ；

（5） $|A^{*}|=|A| ^{n-1}$ ；

（6）若 $A$ 的特征值为 $λ1,λ2,,, λn$ ，则 $\left| A \right|=\prod_{i=1}^{n}\lambda_{i}$ ；

（7）若 $A$ 与 $B$ 相似，则 $|A|=|B|$ ；

克莱姆法则

11、克莱姆法则：

（1）齐次线性方程组的系数行列式不为0，那么方程为唯一解 $x_{j}=\frac{D_{j}}{D},\kern{6pt}j=1,2,...,n$ ； $D$ 是系数系数行列式，其中 $D_{j}$ 是把 $D$ 中第 $j$ 列元素对应地换成常数项而其余各列保持不变所得到的行列式；

（2）如果非齐次线性方程组无解或有两个不同解，则它的系数行列式必为0；

（3）若齐次线性方程组的系数行列式不为0，则齐次线性方程组只有0解；如果方程组有非零解，那么必有 $D=0$ ；

二、矩阵

矩阵的运算

1、矩阵乘法注意事项：

（1）矩阵乘法要求前列后行一致；

（2）矩阵乘法不满足交换律；

（3） $AB=〇$ 不能推出 $A=〇$ 或 $B=〇$ ;

2、转置的性质：

（1） $(A+B)^T =A^T+B^T$

（2） $(kA)^T=kA^T$

（3） $(AB)^T =B^TA^T$

（4） $|A| ^T =|A|$

（5） $(A ^T)^T =A$

矩阵的逆

3、逆的定义： $AB=E$ 或 $BA=E$ 成立，称 $A$ 可逆， $B$ 是 $A$ 的逆矩阵，记为 $B=A^{-1}$ ; 注： $A$ 可逆的充要条件是 $|A| ≠0$ ;

4、逆的性质：

（1） $(kA)^{-1}=\frac{1}{k}·A^{-1} (k≠0)$

（2） $(AB)^{-1}=B^{-1}·A^{ -1}$

（3） $|A^{-1}|=|A|^{-1}$

（4） $(A^{T})^{-1} =(A^{-1})^{T}$

（5） $(A^{-1})^{-1}=A$

5、逆的求法：

（1） $A$ 为抽象矩阵：由定义或性质求解

（2） $A$ 为数字矩阵： $(A|E)→初等行变换→(E|A^{-1})$

（3）如果 $A$ 是可逆矩阵，则可以通过伴随矩阵求解: $A^{-1}=\frac{1}{\left| A \right|}A^{\ast}$

矩阵的初等变换

6、初等行（列）变换定义：

（1）两行（列）互换；

（2）一行（列）乘非零常数 $c$ ;

（3）一行（列）乘 $k$ 加到另一行（列）;

7、初等矩阵：单位矩阵 $E$ 经过一次初等变换得到的矩阵；

8、初等变换与初等矩阵的性质：

（1）初等行（列）变换相当于左（右）乘相应的初等矩阵

（2）初等矩阵均为可逆矩阵，会有

$E_{ij}^{-1}=E_{ij} \kern{6pt} (i,j 两行互换)\\ E_{i}^{-1}(c)=E_{i}(1/c)\kern{6pt}(第 i 行(列)乘 c)\\ E_{ij}^{-1}(k)=E_{ij}(-k)\kern{6pt} (第 i 行乘 k 加到 j)$

矩阵的秩

9、秩的定义：非零子式的最高阶数；

注：

（1） $r(A)=0$ 意味着所有元素为 0，即 $A=〇$ ；

（2） $r(A_{n×n})=n(满秩)\leftrightarrow|A| ≠0\leftrightarrow A 可逆； r(A_{n×n})＜n\leftrightarrow |A|=0 \leftrightarrow A 不可逆；$

（3） $r(A)=r（r=1,2,,,n-1)\leftrightarrow r 阶子式非零且所有 r+1 子式均为 0$ ;

10、秩的性质：

（1） $A$ 为 $m×n$ 阶矩阵，则 $r\left( A \right)\leq min\left( m,n \right)$ ;

（2） $r\left( A\pm B \right)\leq r\left( A \right)+r\left( B \right)$ ;

（3） $r\left( AB \right)\leq min\{ r(A),r(B)\}$ ;

（4） $r(kA)=r(A)（k≠0）$ ;

（5） $r(A)=r(AC)$ ( $C$ 是一个可逆矩阵) ；

（6） $r(A)=r(A^T)=r(A^TA)=r(AA^T)$ ；

（7）设 $A$ 是 $m×n$ 阶矩阵， $B$ 是 $n\times s$ 矩阵， $AB=O$ ，则 $r(A)+r(B)≤n$ ；

11、秩的求法：

（1） $A$ 为抽象矩阵：由定义或性质求解；

（2） $A$ 为数字矩阵： $A\rightarrow初等行变换 →阶梯型$ （每行第一个非零元素下面的元素均为 0），则 $r(A)=非零行的行数$ ；

伴随矩阵

12、伴随矩阵的性质：

（1） $AA^*=A^*A=|A|E \rightarrow A^*=|A|A ^{-1}$

（2） $(kA)^*=k^{n-1}A^*$

（3） $(AB)^*=B^*A^*$

（4） $|A^*|=|A|^{n-1}$

（5） $(A ^T)^*=(A^*)^T$

（6） $(A^ {-1})^*=(A^*)^ {-1}=A|A| ^{-1}$

（7） $(A^*)^*=|A|^{(n-2)}·A$

（8） $r(A^*)=n(r(A)=n)； r(A^*)=1\kern{6pt}(r(A)=n-1)； r(A^*)=0 \kern{6pt}(r(A)＜n-1)$

分块矩阵

13、分块矩阵的乘法：要求前列后行分法相同；

14、分块矩阵求逆：

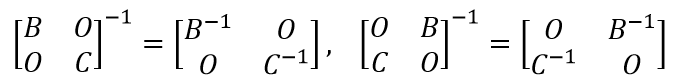
三、向量

向量的概念及运算

1、向量的内积： $(α,β)=α ^Tβ=β ^T α$ ；

2、长度定义： $\left| \left| \alpha \right| \right|=\sqrt{\left( \alpha,\alpha \right)}=\sqrt{\alpha^T\alpha}=\sqrt{a_{1}^{2}+a_{2}^{2}+\cdot\cdot\cdot+a_{n}^{2}}$ ；

3、正交定义： $(α,β)=α ^Tβ=β ^T α=a_1b_1+a_2b_2+,,, +a_nb_n=0$ ；

4、正交矩阵的定义： A 为 n 阶矩阵， $AA^T =E \leftrightarrow A^{-1}=A^T \leftrightarrow A^T A=E \leftrightarrow |A|= ±1$

线性组合和线性表示

5、线性表示的充要条件：非零列向量 $\beta$ 可由 $α_1,α_2,..., α_s$ 线性表示：

（1）非齐次线性方程组 $(α_1,α_2,...,α_s)\left( x_1,x_2,...,x_s \right)^T=\beta$ 有解；

（2） $r(α_1,α_2,...,α_s)=r(α_1,α_2,...,α_s,β)$ 系数矩阵的秩等于增广矩阵的秩；

6、线性表示的充分条件：若 $α_1,α_2,...,α_s$ 线性无关， $α_1,α_2,...,α_s,β$ 线性相关，则 $\beta$ 可由 $α_1,α_2,...,α_s$ 线性表示。

7、线性表示的求法：

设 $α_1,α_2,...,α_s$ 线性无关， $\beta$ 可由其线性表示： $\left( α_1,α_2,...,α_s |\beta\right)\rightarrow$ 初等行变换 $\rightarrow$ （行最简形|系数）；

行最简形：每行第一个非0的数为1，其余元素均为0；

线性相关和线性无关

8、线性相关注意事项：

（1） $\alpha$ 线性相关 $\leftrightarrow$ $\alpha=0$

（2） $α_1,α_2$ 线性相关 $\leftrightarrow$ $α_1,α_2$ 成比例

9、线性相关的充要条件：

向量组 $α_1,α_2,,,α_s$ 线性相关：

（1）有个向量可由其余向量线性表示；

（2）齐次方程 $(α_1,α_2,...,α_s)\left( x_1,x_2,...,x_s \right)^T=0$ 有非零解；

（3） $r(α_1,α_2,...,α_s)<s$ 即秩小于个数；

特别地， $n$ 个 $n$ 维列向量 $α_1,α_2,...,α_n$ 线性相关：

（1） $r(α_1,α_2,...,α_n)<n$

（2） $\left| α_1,α_2,...,α_s \right|=0$

（3） $\left( α_1,α_2,...,α_n \right)$ 不可逆

10、线性相关的充分条件：

（1）向量组含有零向量或成比例的向量必相关；

（2）部分相关，则整体相关；

（3）高维相关，则低维相关；

（4）以少表多，多必相关；

推论： $n+1$ 个 $n$ 维向量一定线性相关。

11、线性无关的充要条件

向量组 $α_1,α_2,...,α_s$ 线性无关：

（1）任意向量均不能由其余向量线性表示；

（2）齐次方程 $(α_1,α_2,...,α_s)\left( x_1,x_2,...,x_s \right)^T=0$ 只有零解；

（3） $r(α_1,α_2,...,α_s)=s$ ；

特别地， $n$ 个 $n$ 维向量 $α_1,α_2,...,α_n$ 线性无关，则 $r(α_1,α_2...,,α_n)=n$ ； $\left| α_1,α_2,...,α_n\right|\ne0$ ；矩阵 $(α_1,α_2,...,α_n)$ 可逆。

12、线性无关的充分条件：

（1）整体无关，部分无关；

（2）低维无关，高维无关；

（3）正交的非零向量组线性无关；

（4）不同特征值的特征向量无关；

13、线性相关、线性无关判定

（1）定义法；

（2）秩：若小于阶数，线性相关；若等于阶数，线性无关；

极大线性无关组与向量组的秩

14、极大线性无关组不唯一；

15、向量组的秩 :极大无关组中向量的个数成为向量组的秩（矩阵的秩 :非零子式的最高阶数）；

注：向量组 $α_1,α_2,...,α_s$ 的秩与矩阵 $A=(α_1,α_2,...,α_s)$ 的秩相等；

16、极大线性无关组的求法

（1） $α_1,α_2,...,α_s$ 为抽象的：定义法

（2） $α_1,α_2,...,α_s$ 为数字的： $(α_1,α_2,...,α_s)\rightarrow$ 初等行变换 $\rightarrow$ 阶梯型矩阵，则每行第一个非零的数对应的列向量构成极大无关组；

向量空间

17、基（就是极大线性无关组）变换公式：若 $α_1,α_2,...,α_n$ 与 $β_1,β_2,...,β_n$ 是 $n$ 维向量空间 $V$ 的两组基，则基变换公式为 $(β_1,β_2,...,β_n)=(\alpha_1,\alpha_2,...,\alpha_n)\cdot C_{n\times n}$ ；其中， $C_{n\times n}$ 是从基式 $α_1,α_2,...,α_n$ 到 $β_1,β_2,...,β_n$ 的过渡矩阵： $C_{n\times n}= (α_1,α_2,...,α_n) ^{-1}\left( \beta_1,\beta_2,...,\beta_n \right)$ .

18、坐标变换公式：向量 $\gamma$ 在基 $α_1,α_2,...,α_n$ 与基 $β_1,β_2,...,β_n$ 的坐标分别为 $x=(x_1,x_2,...,x_n)^T$ ， $y=(y_1,y_2,...,y_n)^T$ ，即 $\gamma=\alpha_{1}x_{1}+\alpha_{2}x_{2}+...+\alpha_{n}x_{n}=\beta_{1}y_{1}+\beta_2y_{2}+...+\beta_ny_{n}$ ，则坐标变换公式为 $x=Cy$ 或 $y=C^{-1}x$ 。其中， $C$ 是从基 $α_1,α_2,...,α_n$ 到 $β_1,β_2,...,β_n$ 的过渡矩阵， $C=\left( α_1,α_2,...,α_n \right)^{-1}\left( \beta_1, \beta_2,...,\beta_n\right)$ ；

Schmidt正交化

19、设 $\alpha_1,\alpha_2,\alpha_3$ 线性无关：

（1）正交化

令 $\beta_1=\alpha_1$ ,则：

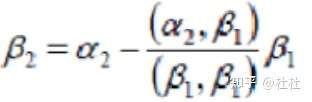
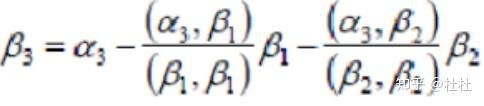
（2）单位化

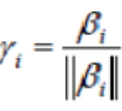
四、线性方程组

方程组的表达形与解向量

1、解的形式：

（1）一般形式

（2）矩阵形式： $Ax=b$ ；

（3）向量形式： $A=(α_1，α_2, ...,α_n)$ ;

2、解的定义：若 $η=（c_1,c_2,...,c_n）^T$ 满足方程组 $Ax=b$ ，即 $A\eta=b$ ，称 $\eta$ 是 $Ax=b$ 的一个解(向量)；

解的判定与性质

3、齐次方程组：

（1）只有零解 —— $r(A)=n$ （ $n$ 为 $A$ 的列数或是未知数 x 的个数）

（2）有非零解 —— $r(A)<n$

4、非齐次方程组：

（1）无解 —— $r\left( A \right)<r\left( A|b \right)$

（2）唯一解 —— $r\left( A \right)=r\left( A|b \right)=n$

（3）无穷多解 —— $r\left( A \right)=r\left( A|b \right)<n$

5、解的性质：

（1）若 $\xi_1,\xi_2$ 是 $Ax=0$ 的解，则 $k_1\xi_1+k_2ξ_2$ 是 $Ax=0$ 的解；

（2）若 $\xi$ 是 $Ax=0$ 的解， $\eta$ 是 $Ax=b$ 的解，则 $\xi+\eta$ 是 $Ax=b$ 的解；

（3）若 $\eta_1,\eta_2$ 是 $Ax=b$ 的解，则 $\eta_1-\eta_2$ 是 $Ax=0$ 的解；

推广：

（1）设 $\eta_1,\eta_2,...,\eta_s$ 是 $Ax=b$ 的解，则当 $\Sigma k_i=1$ , $k_1η_1+k_2η_2+,..., +k_sη_s$ 是 $Ax=b$ 的解；当 $\Sigma k_i = 0$ 是 $Ax=0$ 的解；

（2）设 $\eta_1,\eta_2,...,\eta_s$ 是 $Ax=b$ 的 $s$ 个线性无关的解，则 $\eta_2-\eta_1,\eta_3-\eta_1,...,\eta_s-\eta_1$ 为 $Ax=0$ 的 $s-1$ 个线性无关的解；

基础解系

6、基础解系定义：

（1） $\xi_1,\xi_2,...,\xi_s$ 是 $Ax=0$ 的解；

（2） $\xi_1,\xi_2,...,\xi_s$ 线性无关；

（3） $Ax=0$ 的所有解均可由其线性表示——基础解系即所有解的极大无关组；注：基础解系不唯一。任意 $n-r\left( A \right)$ 个线性无关的解均可作为基础解系；

7、重要结论：

设 $A$ 是 $m×n$ 阶矩阵， $B$ 是 $n×s$ 阶矩阵， $AB=O$

（1）B的列向量均为方程 $Ax=0$ 的解；

（2） $r(A)+r(B)≤n$ ;

8、基础解系的求法

（1） $A$ 为抽象的：由定义或性质凑 $n-r(A)$ 个线性无关的解

（2） $A$ 为数字的： $A$ $\rightarrow$ 初等行变换 $\rightarrow$ 阶梯型

解的结构（通解）

9、齐次线性方程组的通解（所有解）

设 $r(A)=r$ ， $ξ_{1}，ξ_{2},..., ξ_{n-r}$ 为 $Ax=0$ 的基础解系，则 $Ax=0$ 的通解为 $k_1η_1+k_2η_2+... +k_{n-r}η_{n-r}$ （其中 $k_1,k_2,...k_{n-r}$ 为任意常数）;

10、非齐次线性方程组的通解

设 $r(A)=r$ ， $ξ_{1}，ξ_{2},..., ξ_{n-r}$ 为 $Ax=0$ 的基础解系， $η$ 为 $Ax=b$ 的特解，则 $Ax=b$ 的通解为 $η+ k_1η_1+k_2η_2+, +k_{n-r}η_{n-r}$ （其中 $k_1,k_2,...,k_{n-r}$ 为任意常数）;

公共解与同解

11、公共解定义：如果 $\alpha$ 既是方程组 $Ax=0$ 的解，又是方程组 $Bx=0$ 的解，则称 $α$ 为其公共解；

12、非零公共解的充要条件：方程组 $Ax=0$ 与 $Bx=0$ ,

13、重要结论

（1）设 $A$ 是 $m×n$ 阶矩阵，则齐次方程 $A^TAx=0$ 与 $Ax=0$ 同解， $r(A^TA)=r(A)$ ；

（2）设 $A$ 是 $m×n$ 阶矩阵， $r(A)=n$ ， $B$ 是 $n×s$ 阶矩阵，则齐次方程 $ABx=0$ 与 $Bx=0$ 同解， $r(AB)=r(B)$ ；

五、特征值与特征向量

矩阵的特征值与特征向量

1、特征值、特征向量的定义：设 $A$ 为 $n$ 阶矩阵，如果存在数 $\lambda$ 及非零列向量 $\alpha$ ，使得 $Aα=λα$ ，称 $α$ 是矩阵 $A$ 属于特征值 $λ$ 的特征向量。

2、特征多项式、特征方程的定义： $| λE-A|$ 称为矩阵 $A$ 的特征多项式（ $λ$ 的 $n$ 次多项式）。 $| λE-A |=0$ 称为矩阵 $A$ 的特征方程（ $λ$ 的 $n$ 次方程）。注:特征方程可以写为 $|A- λE|=0$ ；

注：特征方程可以写为 $|A- λE|=0$

3、重要结论：

（1）若 $\alpha$ 为齐次方程 $Ax=0$ 的非零解，则 $Aα=0·α$ ，即 $α$ 为矩阵 $A$ 特征值 $λ=0$ 的特征向量；

（2） $A$ 的各行元素和为 $k$ ，则 $(1,1,...,1)^T$ 为特征值为 $k$ 的特征向量；

（3）上（下）三角或主对角的矩阵的特征值为主对角线各元素；

4、特征值与特征向量的求法

（1） $A$ 为抽象的：由定义或性质求解；

（2） $A$ 为数字的：由特征方程法求解；

5、特征方程法

（1）解特征方程 $|A- λE|=0$ ，得矩阵 $A$ 的 $n$ 个特征值 $λ_{1},λ_{2},...,λ_n$ ；注： $n$ 次方程必须有 $n$ 个根（可有多重根，写作 $λ1=λ2=, ...,=λs=实数$ ，不能省略）；

（2）解齐次方程 $(λ_{i}E-A)=0$ ，得属于特征值 $λ_{i}$ 的线性无关的特征向量，即其基础解系（共 $n-r(\lambda_{i}E-A)$ 个解）；

6、性质

（1）不同特征值的特征向量线性无关；

（2） $k$ 重特征值最多 $k$ 个线性无关的特征向量： $1≤n-r(λ_{i}E-A)≤k_{i}$ ；

（3）设 $A$ 的特征值为 $λ_1,λ_2,...,λ_n$ ，则 $\left| A \right|=\Pi\lambda_{i},\kern{4pt} \Sigma\lambda_{i}=\Sigma a_{ii}=tr(A)$ ；

（4）当 $r(A)=1$ ，即 $A=αβ^T$ ，其中 $α,β$ 均为 $n$ 维非零列向量，则 $A$ 的特征值为 $\lambda_{1}=\Sigma a_{ii}=\alpha\beta^T=\beta^T\alpha,\kern{4pt}\lambda_2=,...,=\lambda_n=0$ ；

相似矩阵

7、相似矩阵的定义：设 $A、B$ 均为 $n$ 阶矩阵，如果存在可逆矩阵 $P$ 使得 $B=P^{-1}AP$ ，称 $A$ 与 $B$ 相似，记作 $A\sim B$ ；

8、相似矩阵的性质：

（1）若 $A$ 与 $B$ 相似，则 $f(A)$ 与 $f(B)$ 相似；

（2）若 $A$ 与 $B$ 相似， $B$ 与 $C$ 相似，则 $A$ 与 $C$ 相似；

（3）相似矩阵有相同的行列式、秩、特征多项式、特征方程、特征值、迹（即主对角线元素之和）；

（4）若 $A$ 与 $B$ 相似，则 $AB$ 与 $BA$ 相似， $A^T$ 与 $B^T$ 相似， $A^{ -1}$ 与 $B^{ -1}$ 相似， $A^*$ 与 $B^*$ 也相似；

矩阵的相似对角化

9、相似对角化定义：

如果 $A$ 与对角矩阵相似，即存在可逆矩阵 $P$ ，使得

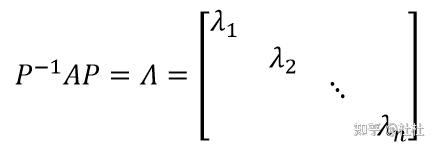
称 A 可相似对角化。

注： $Aα_i=λ_iα_i（α_i≠0，由于 P 可逆）$ ，故 $P$ 的每一列均为矩阵 $A$ 的特征值 $λ_i$ 的特征向量；

10、相似对角化的充要条件

（1） $A$ 有 $n$ 个线性无关的特征向量；

（2） $A$ 的 $k$ 重特征值有 $k$ 个线性无关的特征向量；

11、相似对角化的充分条件：

（1） $A$ 有 $n$ 个不同的特征值（不同特征值的特征向量线性无关）；

（2） $A$ 为实对称矩阵；

12、重要结论：

（1）若 $A$ 可相似对角化，则 $r(A)$ 为非零特征值的个数， $n-r(A)$ 为零特征值的个数；

（2）若 $A$ 不可相似对角化， $r(A)$ 不一定为非零特征值的个数；

实对称矩阵

13、性质

（1）特征值全为实数；

（2）不同特征值的特征向量正交；

（3） $A$ 可相似对角化，即存在可逆矩阵 $P$ 使得 $P^{-1}AP=Λ$ ；

（4） $A$ 可正交相似对角化，即存在正交矩阵 $Q$ ，使得 $Q^{-1}AQ=Q^TAQ=Λ$ ；

六、二次型

二次型及其标准形

1、二次型：

（1）一般形式

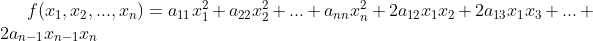
（2）矩阵形式（常用）： $Q\left( x \right)=x^TAx$

2、标准形：如果二次型只含平方项，即 $f(x_1,x_2,...,x_n)=d_1x_{1}^{2} +d_2x_{2}^{2}+,...,+d_nx_{n}^{2}$ 这样的二次型称为标准形（对角线）；

3、二次型化为标准形的方法：

（1）配方法：通过可逆线性变换 $x=Cy\kern{6pt}(C 可逆)$ ，将二次型化为标准形。其中，可逆线性变换及标准形通过先配方再换元得到。

（2）正交变换法：通过正交变换 $x=Qy$ ，将二次型化为标准形 $λ_1y_{12} +λ_2y_{22} +,...,+λ_ny_{n2}$ ，其中， $λ_1，λ_2,...,λ_n$ 是 $A$ 的 $n$ 个特征值， $Q$ 为 $A$ 的正交矩阵；注：正交矩阵 $Q$ 不唯一， $γ_i$ 与 $λ_{i}$ 对应即可。

惯性定理及规范型

4、定义：

正惯性指数：标准形中正平方项的个数称为正惯性指数，记为p；

负惯性指数：标准形中负平方项的个数称为负惯性指数，记为q；

规范型：规范型中系数1的个数等于正特征值的个数 (或二次型正惯性指数)，规范型中系数-1的个数等于负特征值的个数 (或二次型负惯性指数)。不考虑+1， -1 顺序的情况下，规范型是唯一的；

5、惯性定理：二次型无论选取怎样的可逆线性变换为标准形，其正负惯性指数不变。

注：

（1）由于正负惯性指数不变，所以规范形唯一；

（2） $p$ =正特征值的个数， $q$ =负特征值的个数， $p+q$ =非零特征值的个数 $=r(A)$ ；

合同矩阵

6、定义： $A、B$ 均为 $n$ 阶实对称矩阵，若存在可逆矩阵 $C$ ，使得 $B=C^T AC$ ，称 $A$ 与 $B$ 合同；

7、 $n$ 阶实对称矩阵 $A、B$ 的关系

（1） $A,B$ 相似 $(B=P^{-1}AP)\leftrightarrow 相同的特征值$

（2） $A,B$ 合同 $(B=C^TAC) \leftrightarrow 相同的正负惯性指数\leftrightarrow相同的正负特征值的个数$

（3） $A,B等价（B=PAQ）\leftrightarrow r(A)=r(B)$

注：实对称矩阵相似必合同，合同必等价；

正定二次型与正定矩阵

8、正定的定义：二次型 $x^TAx$ ，如果任意 $x≠0$ ，恒有 $x ^T Ax＞0$ ，则称二次型正定，并称实对称矩阵 $A$ 是正定矩阵；

9、 $n$ 元二次型 $x^TAx$ 正定充要条件：

（1） $A$ 的正惯性指数为 $n$ ；

（2） $A$ 与 $E$ 合同，即存在可逆矩阵 $C$ ，使得 $A=C^TC$ 或 $C^T AC=E$ ；

（3） $A$ 的特征值均大于 0 ；

（4） $A$ 的顺序主子式均大于 0（ $k$ 阶顺序主子式为前 $k$ 行前 $k$ 列的行列式）；

10、 $n$ 元二次型 $x^T Ax$ 正定必要条件：

（1） $a_{ii}＞0$

（2） $|A| ＞0$

11、重要结论：

（1）若 $A$ 是正定矩阵，则 $kA（k＞0）,A^ k,A^ T，A^{ -1},A^*$ 正定

（2）若 $A,B$ 均为正定矩阵，则 $A+B$ 正定
相关阅读:
SpringBoot的启动Banner定制 IT
idea重启 IT
IDEA快捷键总结 IT
java8的List排序 IT
树数据处理
 antd 默认展开的三种实现方式
 antd input placeholder颜色样式修改
 react ref 用法案例
 audtomake
yocto相关
原文地址：https://www.cnblogs.com/bruce1992/p/16513903.html

《线性代数》知识点汇总

行列式概念和性质

重要行列式

按行（列）展开

行列式公式

克莱姆法则

二、矩阵

矩阵的运算

矩阵的逆

矩阵的初等变换

矩阵的秩

伴随矩阵

分块矩阵

三、向量

向量的概念及运算

线性组合和线性表示

线性相关和线性无关

极大线性无关组与向量组的秩

向量空间

Schmidt正交化

四、线性方程组

方程组的表达形与解向量

解的判定与性质

基础解系

解的结构（通解）

公共解与同解

五、特征值与特征向量

矩阵的特征值与特征向量

相似矩阵

矩阵的相似对角化

实对称矩阵

六、二次型

二次型及其标准形

惯性定理及规范型

合同矩阵

正定二次型与正定矩阵