1. 基于灰度值的模板匹配
模板匹配是通过计算模板与图像之间的相似度实现。
1.1. SAD & SSD
最简单的相似度量方法是计算模板与图像之间差值的绝对值的总和(SAD)或所有差值的平方和(SSD)。它们的等式分别为:
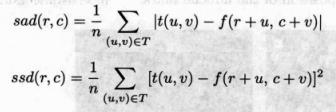

在光照情况保持不变的情况下,SAD和SSD相似度量的结果非常好。但是如果光照发生变化,甚至
在图像中存在相同物体的情况下,他们都将返回非常大的结果。
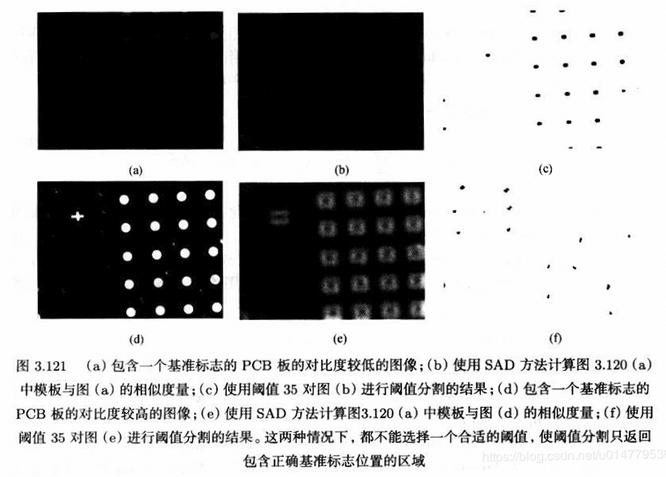
从上面的例子中我们可以看出,SAD和SSD相似度量只有在光照情况不发生变化的情况下可以使用。
在不能保证光照稳定的情况下,必须使用另外一种相似度量方法。理想的情况下,这个相似度量应该不随任何线性的光照变化而变化。
1.2. NCC
能够达到这种要求的一种相似度量是 归一化互相关系数 (NCC),等式为:


只有在 |nc(r,c)| = 1 的情况下,模板与图像之间才完全匹配。一般情况下,归一化互相关系数的绝对值越大就表示模板与正在检测的部分图像之间越接近,归一化互相关系数的绝对值越接近零就表示模板与图像越不一致。

1.3. (提前)终止标准
在上述讨论中,我们假设必须对所有平移位置都计算相似度量。事实上这样做是不必要的,因为计算相似度量的结果将在随后使用阈值 t 进行阈值分割。例如将等式(3.133)求出的SAD结果进行阈值分割意味着我们需要:
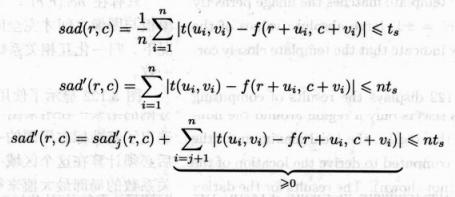

上面提到的停止标准可以使我们在确定不可能达到阅值的情况下停止相似度量的计算。因此,他们除了位姿区间中不必要的部分。事实上,目前改进裁减搜索区间方法的研究仍在积极地进行中。例如,在文献[125]中介绍了使用归一化互相关系数时如何进一步优化裁减搜索区间的方法。在文献[126]和[127]中讨论了使用SAD或SSD时裁减搜索区间的策略。他们首先将图像转换为另一种表示方法,使用这种表示方法时SAD和SSD的一大部分可以使用非常少的计算得到,因此计算中可以尽可能快地达到停止标准。
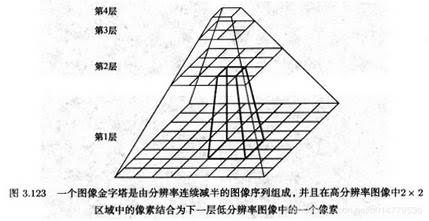
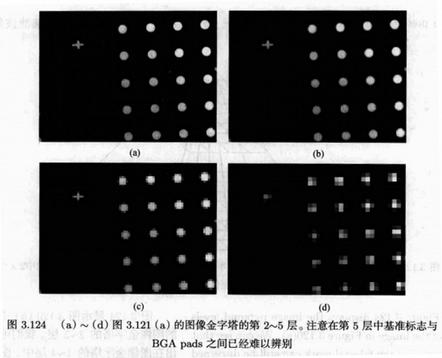
2. 图形金字塔加速匹配
使用上述讨论的停止标准的情况下,在整个图像中计算相似度量也是一个非常耗时的工作。 如果不使用停止标准, 那么算法的复杂度为O(whn) 其中ω和h是图像的宽和高,n是模板中点的数量。使用停止标准一般情况下可以提速的比例为一个常数,但是并不能改变算法复杂度。因此 为了能够在图像中实时找到模板,有必要提出能够进一步提高搜索速度的方法。


3. 基于灰度值的亚像素精度匹配
目前为止, 我们通过匹配得到的模板位置为像素精度。这个位置是通过提取相似度量的局部最大值(SAD,SSD)或局部最小值(NCC)得到。为了使得到的模板位姿的准确度更高,可以提取亚像素精度的局部最小值或最大值。我们只需要将在局部最小值或最大值附近 3×3 的邻域内的相似度量拟合为一个。然后求解得到该多项式的局部最大值或最小值。
另外一种方法是在模板和图像灰度值之间使用最小二乘匹配。由于灰度值之间的最小二乘匹配会受光照变化的影响,因此必须为光照变化建立明确的模型,并且它们的参数必须在最小二乘法拟合中确定,从而使算法不受光照变化影响。
4. 带旋转与缩放的模板匹配
前面的算法,我们将模板匹配限定为模板与图像中的目标物体方向与尺寸一致的情况,也就是说可能位姿的空间被限定为平移的空间。上面我们讨论到的相似度量方法只能够容忍图像中的目标物有很小的旋转和缩放。因此,如果图像中目标物体的方向或大小与模板中不同,那么该目标物体将不能被找到。如果我们希望处理更多类型的变换,例如刚性变换或相似变换,就必须更新匹配方法。为了简单起见,我们将只讨论存在旋转的情况,但这个方法也可以扩展到存在缩放的情况,甚至类似的广义变换。
5. 可靠的模板匹配算法
很多年来,机器视觉应用中都选用上面讨论的模板匹配算法。然而,最近越来越多的应用中要求就算在目标物体由于遮挡或其他方式的干扰导致只有部分出现在图像中时也能找到模板的位置。另外,甚至在目标物体本身存在大的干扰的情况下也能够找到目标物体的位置。这些干扰通常称为混乱。另外在图像中存在严重的非线性光照变化时,也应该能够找到目标物体。
目前为止我们讨论的基于灰度值的模板匹配算法不能够处理这些类型的干扰。因此,这章节中剩余的部分我们将讨论几种其他的方法,使用这些方法可以在存在遮挡、棍乱和非线性光照变化的情况下找到目标物体。
5.1. 基于边缘(SED)
我们已经在3.7节中提到了一个不会受非线性光照变化影响的特性:图像中的边缘不会(至少很少)受光线变化的影响。因此,它们经常被应用在可靠的模板匹配算法中。使用边缘时的唯一问题就是如何选择合适的值来分割边缘。如果这个阈值太小,那么图像中将会有非常多乱七八椭的边缘。如果这个阈值太大,目标物体的重要的边缘可能丢失,这种情况与物体发生遮挡时效果相同。由于这个阈值不可能选择的非常完美,这就是为什么需要匹配算法足够可靠能够处理遮挡和混乱情况。
使用边缘匹配物体存在几种策略:
首先,我们可以在匹配中使用原始的边缘点,或者增加每个点的一些特性(图3.127(b))。另外一种策略是使用3.8.4节中介绍的算法将边缘分割为多个几何基元,然后在图像中匹配这些分割得到的几何基元(图3.127(c))。最后一种策略是基于边缘的分割,我们可以得到边缘上的突变点然后在图像中匹配这些突变点(图3.127(d))。应该注意的是这些突变点可以直接从图像中提取,而不需要首先提取边缘。

边缘匹配算法中的一大类是基于模板边缘与图像边缘之间的距离。这些算法一般使用原始边缘点进行匹配。一个基于这种想法的非常普通的相似度量,是使模板边缘点与离它最近的图像边缘点之间的均方距离最小。因此,显然我们必须为模板边缘上每个点确定离它最近的图像边缘点,这个过程非常的耗时。
幸运的是,由于我们感兴趣的是与最近图像边缘点之间的距离,而不需要知道哪个点是最近的点,因此可是使用一种效率很高的方式,就是计算分割后搜索图像背景的距离变换。如果模板边缘点与图像边缘点之间的平均距离小于一个阈值,我们就认为找到了一个模板的实例。当然,为了得到模板的唯一位置,我们必须计算相似度量的局部最小值。
现在我们可以问自己SED方法是否满足上述可靠模板匹配算法的标准。由于它基于边缘进行匹配,因此不受任意光照变化的影响。另外,由于混乱(也就是搜索图像中其他的边缘)只能减少与搜索图像中最近边缘之间的距离,因此算法不受混乱影响。但是,如果部分边缘在搜索图像中没有出现,没有出现的部分模板边缘与最近图像边缘之间的距离可能会非常大,因此可能在图像中就找不到模板位置。这种情况可见图3.128。想象在一些边缘没有出现的的图像(图3.128(c)和图3.128(d))中搜索图3.128(a)中模板时会发生什么情况。这时没有出现的部分边缘将有一个非常大的平方距离,这将大大增加均方边缘距离的值。此时在图像中找到正确的匹配位置就非常困难。

5.2. Hausdorff算法
由于SED方法的上述问题,因此提出了一种可以应用在边缘匹配算法中的另一种距离。它们是基于两个点集之间的 Hausdorff 距离。让我们将模
板中边缘点表示为T,并且将图像中
边缘点表示为E。然后,这两个点集之间的 Hausdorff 距离可以表示为:

其中
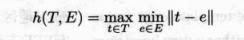
Hausdorff 距离需要非常大的计算量,另外,匹配过程中也会产生巨大的运算负载。而更为关键的,是即便图像中待搜索的的模板实例只存在稍许的遮挡,也会导致在图像中找到很多的错误实例。
5.3. 广义霍夫变换
另外一种基于边缘像素点本身搜索目标物体的算法是由Ballard提出的广义霍夫变换。原始霍夫变换是定义为在分割后的边缘中寻找直线的一种方法。后来霍夫变换经过扩展可以用来检测其他可解析描述的形状,如圆或椭圆。广义霍夫变换的原理可以通过一个简单例子来解释。如果我们试着在一个边缘图像中寻找一个已知半径的圆。因为圆是旋转对称的,这种情况只需要考虑平移。如果希望能够在边缘图像中尽可能迅速地找到圆的位置,我们可以注意到比背景亮的圆,它的边缘的梯度向量垂直与圆的边界,并且梯度向量的方向指向圆的中心。如果圆比背景更暗,梯度向量方向则是背离圆的中心向外。因此,由于我们已知圆的半径,理论上我们就可以从圆上单个点确定圆的中心。
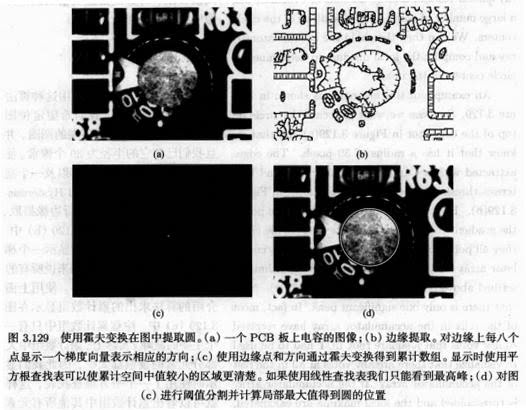
从上面例子中可以看出,我们可以在图像中非常高效地找到圆的位置。如果已知圆的极性,也就是知道它比背景暗还是亮,此时我们只需要在图像中每个边缘点处对累计数组执行一个简单加法即可。如果事先不知道边缘的极性,我们只需要在每个边缘点处执行两个加法即可。因此,算法的运算时间与图像中边缘点数量成比例,而与模板大小无关,也就是与圆大小无关。理想情况下,我们当然希望能够找到一种搜索任意目标物体的算法可以达到同样的效率。
上述讨论的广义霍夫变换效率已经非常高。平均起来,它增加固定数量的累计数组元素。因此,它的运行时间只取决于图像中边缘点的数量。然而,这种算法对于机器视觉应用还是不够快,因为用来搜索对象的累计空间会在很短时间内变的非常大,尤其在允许目标物体旋转或缩放的应
用中。另外,这个累计器还需要一个巨大的存储空间。
针对这种情况,在【[论文(2003): Real-time object recognition using a modified generalized Hough transform](数字图像处理-模板匹配/Real-time object recognition using a modified generalized Hough transform.pdf)】中提出了一种分级的广义霍夫变换。它使用图像金字塔加速搜素,通过利用金字塔高层中找到的匹配位置约東金字塔低层的搜索空间来减少累计数组的尺寸。使用这种分级广义霍夫变换,可以在图像中实时找到目标物体,并且图像中存在遮挡、混乱和几乎任意光照变化的情况下算法都非常稳定。
5.4. 基于匹配几何基元
目前为止,上面讨论的这些算法都是基于直接匹配边缘上的点。另一类边缘匹配算法基于匹配几何基元,例如点、线、圆。这些算法一般是猜测和测试的组合,也就是一般为少数几何基元假设一个匹配位置,然后测试这些假定的匹配位置在图像中有没有足够的证据。
这种类型算法的最大挑战就是它必须解决指数级的复杂度问题。