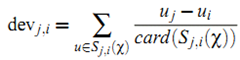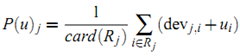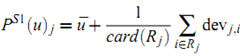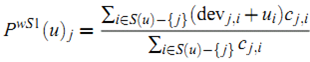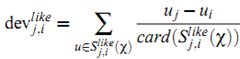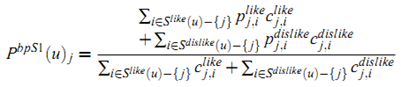[[ 本文地址:http://www.cnblogs.com/breezedeus/archive/2011/03/11/1981781.html
转载请注明出处 ]]
Slope One 是一种很好理解的推荐算法,因为它的简单性而备受关注。网上有很多相关的博文介绍它的原理,但很少见到比较全面而且数学性比较强的介绍。我下面主要从数学的角度比较全面的介绍相关的三个算法。里面使用红色标记的文字是我自己的感想,欢迎大家的指正。
一些很好的参考文献
- 算法提出的 paper:Slope One Predictors for Online Rating-Based Collaborative Filtering, Daniel Lemire, Anna Maclachlan, 2005
- 一个转载的中文博客:http://www.cppblog.com/AutomateProgram/archive/2010/07/19/120790.html
- 一个转载的详细介绍利用python实现Slope One的博客:http://blog.csdn.net/Java2King/archive/2010/03/14/5378597.aspx
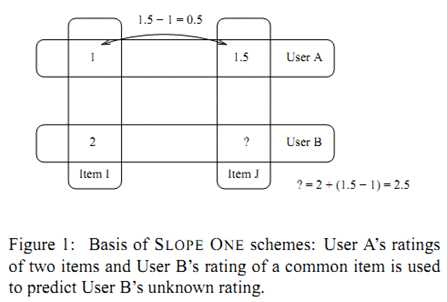
论文作者们试图建立满足如下性质的robust推荐算法:
1. 算法容易实现和维护
2. 对新的评分应该立即给予响应
3. 查询速度要快(虽然可能以牺牲存储量为代价)
4. 对新的用户也要能给出有效的推荐
5. 精度上要有竞争力
他们提出了三个算法,
Slope One
其基本的想法来自于简单的一元线性模型 $w = f(v) = v + b$。已知一组训练点 ${(v_i, w_i)}_{i=1}^n$,利用此线性模型最小化预测误差的平方和,我们可以获得
利用上式获得了$b$的取值后,对于新的数据点$v_{new}$,我们可以利用 $w_{new} = b + v_{new}$ 获得它的预测值。
直观上我们可以把上面求偏移 $b$ 的公式理解为 $w_i$ 和 $v_i$ 差值的平均值。
利用上面的直观,我们定义item $i$ 相对于 item $j$ 的平均偏差:
其中 $S_{j,i}()$ 表示同时对item $i$ 和 $j$ 给予了评分的用户集合,而 $card()$ 表示集合包含的元素数量。
有了上面的定义后,我们可以使用 ![]() 获得用户 $u$ 对 item $j$ 的预测值。当把所有这种可能的预测平均起来,可以得到:
获得用户 $u$ 对 item $j$ 的预测值。当把所有这种可能的预测平均起来,可以得到:
其中 $R_j$ 表示所有用户 $u$ 已经给予评分且满足条件 ($i \neq j$ 且 $S_{j,i}$非空) 的item集合。
对于足够稠密的数据集,我们可以使用近似
把上面的预测公式简化为
Weighted Slope One
Slope One中在计算 item $i$ 相对于 item $j$ 的平均偏差 $dev_{j,i}$ 时没有考虑到使用不同的用户数量平均得到的 $dev_{j,i}$,其可信度不同。假设有 $2000$ 个用户同时评分了 item $j$ 和 $k$,而只有$20$ 个用户同时评分了 item $j$ 和 $l$,那么显然获得的 $dev_{j, k}$ 比 $dev_{j, l}$ 更具有说服力(类似于kNN中压缩相似度的思想)。所以一个修正是对最终的平均使用加权:
其中
(根据在Netflix上的经验,可能把 $c_{j,i}$ 再开方更合适)
Bi-Polar Slope One
Bi-Polar Slope One 进一步把用户已经给予评分的item划分为两类——like和dislike,而其划分的方法是判断对应的评分是否大于此用户的平均评分:
类似地,可以定义对item $i$ 和 $j$ 具有相同喜好的用户集合:
利用上面的定义,我们可以使用下面的公式为(like或dislike的item)获得新的偏差值:
这样可以计算从item $i$ 计算得到的预测值:
最终 Bi-Polar Slope One 的预测公式为
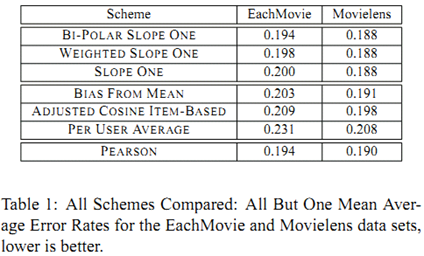
最后的实验比较使用的度量为 MAE,其结果如下:
一些自己的想法:
1). Slope One 是基于一元线性模型 $w = f(v) = v + b$,那么是否可以使用多元线性组合?比如可以先利用关联规则方法获得一些关联规则,然后对于找出的每个关联规则使用线性模型。作者在文中也提到可以尝试使用二次或更高次的回归模型。显然这些做法都会让整个模型更加复杂。
2). 在具体应用中,Weighted Slope One 中的 weight 的选取应该可以找到更好的方法
3). 在 Bi-Polar Slope One 中,作者只是简单地使用用户的平均评分来判断like和dislike,这应该会引入比较大的误差。用户的评分往往会随着时间的不同而变动很大,是否可以学习一个更加合理的分割阈值(如 $r + r_u + r_j$)?还有,是否可以把这种binary的分割更加细化,分为三类,乃至更多类……