1、前言
学习数据结构的时候就已经了解了DFS原理,但是一直没有详细的复习和代码实现。再刷题的过程中发现很多题目都使用DFS,因此回头再好好梳理一下DFS的思路以及代码实现。
2、算法理论
2.1 理论知识
深度优先搜索算法(英语:Depth-First-Search,简称DFS)是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。
深度优先遍历的主要思想就是:首先以一个未被访问过的顶点作为起始顶点,沿当前顶点的边走到未访问过的顶点;当没有未访问过的顶点时,则回到上一个顶点,继续试探访问别的顶点,直到所有的顶点都被访问。沿着某条路径遍历直到末端,然后回溯,再沿着另一条进行同样的遍历,直到所有的顶点都被访问过为止。
2.2 举例
求图中v0出发,到达v6长度为4的路径是否存在。
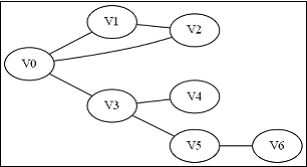
DFS过程:
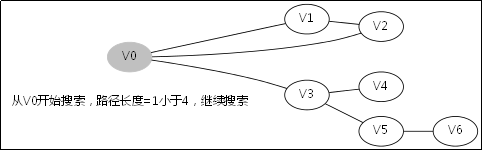
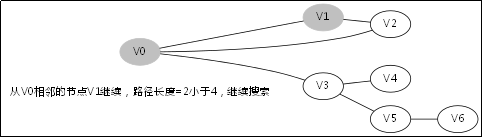
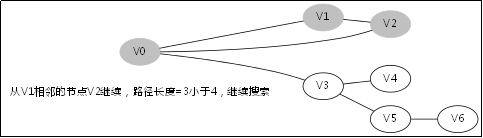
。。。。。
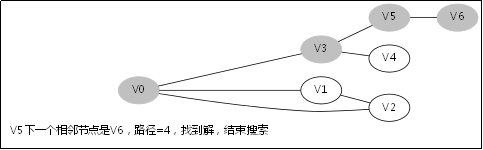
上例参考rapheal大神的例子,具体过程不详细展示了。上例展示了DFS如何直观的解决搜索问题。
3、算法实现
代码框架:
DFS(dep , ...){ //dep代表目前DFS深度
if(找到解 || 走不下去了) //走不下去就是visited[dep] == 1了。
{
...;
return;
}
DFS(dep+1, ...) //枚举下一种情况
visited[dep] = 0 //回退时标记回退的节点为未被访问的节点
}
通常DFS要有一个visited数组,用来标识某个节点是否被访问过,但是也不是一定的。在走迷宫的题目中,就是用stack来标识。
感觉DFS一定要有递归的基础, DFS只处理当前的状态节点n,不关注下一个状态。