题目链接:http://codeforces.com/contest/828/problem/D
必须是一棵树!大体思路就是按照画同心圆的方法给排列出来,一号作为圆心一层一层向外扩展。
证明的话还得想想。。。
代码:
1 int n, k; 2 3 int main(){ 4 scanf("%d %d", &n, &k); 5 int t = (n - 1) / k - 1, x = (n - 1) % k; 6 int ans = 0; 7 if(x == 0) ans = 2 * t + 2; 8 else if(x == 1) ans = 2 * t + 3; 9 else ans = 2 * t + 4; 10 printf("%d ", ans); 11 12 for(int i = 1; i <= k; i++){ 13 printf("1 %d ", i + 1); 14 } 15 for(int i = 2; i <= n - k; i++){ 16 printf("%d %d ", i, i + k); 17 } 18 19 }
题目:
Arkady needs your help again! This time he decided to build his own high-speed Internet exchange point. It should consist of n nodes connected with minimum possible number of wires into one network (a wire directly connects two nodes). Exactly k of the nodes should be exit-nodes, that means that each of them should be connected to exactly one other node of the network, while all other nodes should be connected to at least two nodes in order to increase the system stability.
Arkady wants to make the system as fast as possible, so he wants to minimize the maximum distance between two exit-nodes. The distance between two nodes is the number of wires a package needs to go through between those two nodes.
Help Arkady to find such a way to build the network that the distance between the two most distant exit-nodes is as small as possible.
The first line contains two integers n and k (3 ≤ n ≤ 2·105, 2 ≤ k ≤ n - 1) — the total number of nodes and the number of exit-nodes.
Note that it is always possible to build at least one network with n nodes and k exit-nodes within the given constraints.
In the first line print the minimum possible distance between the two most distant exit-nodes. In each of the next n - 1 lines print two integers: the ids of the nodes connected by a wire. The description of each wire should be printed exactly once. You can print wires and wires' ends in arbitrary order. The nodes should be numbered from 1 to n. Exit-nodes can have any ids.
If there are multiple answers, print any of them.
3 2
2
1 2
2 3
5 3
3
1 2
2 3
3 4
3 5
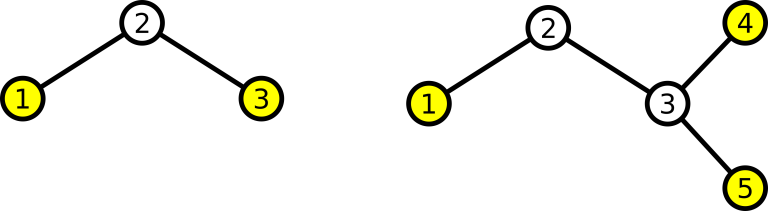
In the first example the only network is shown on the left picture.
In the second example one of optimal networks is shown on the right picture.
Exit-nodes are highlighted.