当遇到交换两个变量的时候,我们通常使用的是借助第三方变量实现两个数的交换。那么如果不使用第三方变量时,该怎么操作呢。
下面有三种方法:
1、通过已有的两个变量之间的加或减实现:
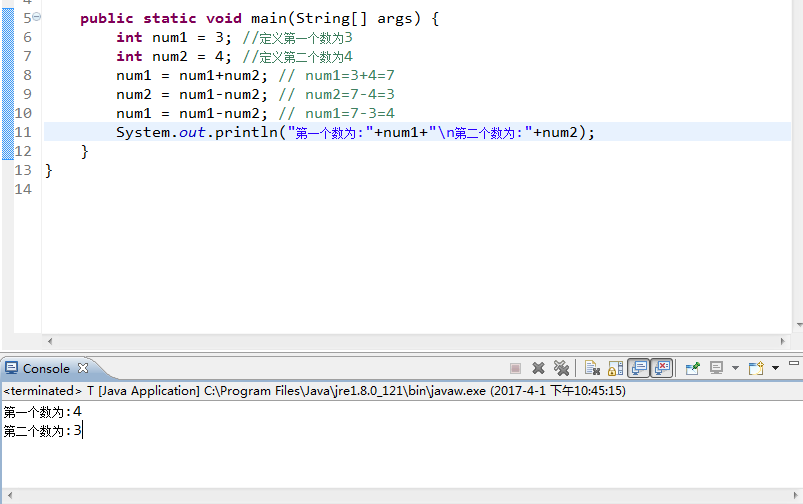
这种方法对于两个都是无限接进int取值范围,而相加超出int取值范围的情况不适用。
2、通过异或实现(异或符号为^)
*******************************************************************************************************
关于^:
异或的运算法则,相当于不带进位的二进制加法。二进制下用1表示真,0表示假,则异或的运算法则为:0异或0=0,1异或0=1,0异或1=1,1异或1=0(同为0,异为1),这些法则与加法是相同的,只是不带进位。
| 第一个数 | 符号 | 第二个数 | 结果 |
| 0 | ^ | 0 | 0 |
| 0 | ^ | 1 | 1 |
| 1 | ^ | 0 | 1 |
| 1 | ^ | 1 | 0 |
如:
num1 = 5,对应的二进制为(101); num2 = 7,对应的二进制为(111);
num1=num1^num2=2; 即二的平方位1^1=0,二的一次方位0^1=1,二的0次方位1^1=0;得到(010)即为2。
num2 = num1 ^ num2=5 ;相当于num2=num1^num2^num2;二的平方位1^1^1=1(此处无论num2的二的平方位是0还是1,异或运算后都为0,故得到的肯定与原num1的二的平方位相同,同理其他位置全部也都是原num1的数);二的一次方位0^1^1=0;二的0次方位1^1^1=1.;得到(101)即为5.
num1 = num1^num2=7; 相当于num1 = num1^num2^num1^num2^num2=num2=7.
此方法同样实现了两个数互换。
*******************************************************************************************************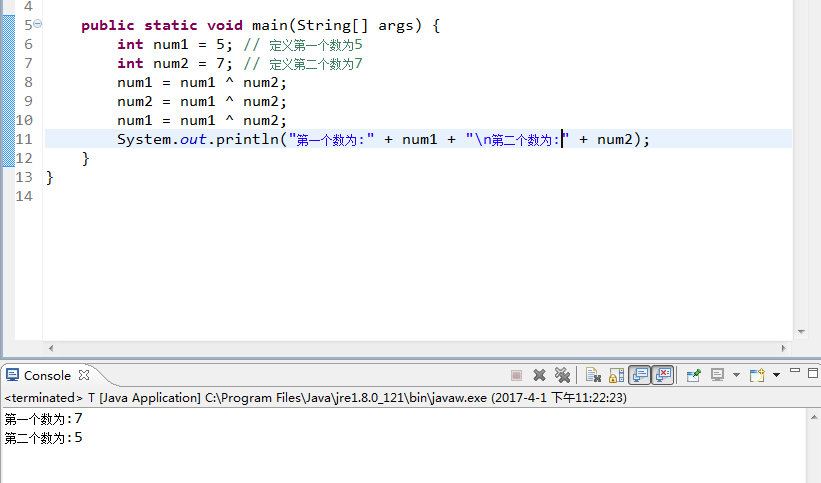
由于^符号是不进位的,所以即使两个都无限接进int取值范围的数。通过^运算,也不会超过int取值范围。
3. 指针地址操作
因为对地址的操作实际上进行的是整数运算,比如:两个地址相减得到一个整数,表示两个变量在内存中的储存位置隔了多少个字节;地址和一个整数相加即“a+10”表示以a为基地址的在a后10个a类数据单元的地址。所以理论上可以通过和算术算法类似的运算来完成地址的交换,从而达到交换变量的目的。即:
int *a,*b; //假设
*a=new int(10);
*b=new int(20); //&a=0x00001000h,&b=0x00001200h
a=(int*)(b-a); //&a=0x00000200h,&b=0x00001200h
b=(int*)(b-a); //&a=0x00000200h,&b=0x00001000h
a=(int*)(b+int(a)); //&a=0x00001200h,&b=0x00001000h
通过以上运算a、b的地址真的已经完成了交换,且a指向了原先b指向的值,b指向原先a指向的值了吗?上面的代码可以通过编译,但是执行结果却令人匪夷所思!原因何在?
首先必须了解,操作系统把内存分为几个区域:系统代码/数据区、应用程序代码/数据区、堆栈区、全局数据区等等。在编译源程序时,常量、全局变量等都放入全局数据区,局部变量、动态变量则放入堆栈区。这样当算法执行到“a=(int*)(b-a)”时,a的值并不是0x00000200h,而是要加上变量a所在内存区的基地址,实际的结果是:0x008f0200h,其中0x008f即为基地址,0200即为a在该内存区的位移。它是由编译器自动添加的。因此导致以后的地址计算均不正确,使得a,b指向所在区的其他内存单元。再次,地址运算不能出现负数,即当a的地址大于b的地址时,b-a<0,系统自动采用补码的形式表示负的位移,由此会产生错误,导致与前面同样的结果。
有办法解决吗?当然!以下是改进的算法:
if(a<b)
{
a=(int*)(b-a);
b=(int*)(b-(int(a)&0x0000ffff));
a=(int*)(b+(int(a)&0x0000ffff));
}
else
{
b=(int*)(a-b);
a=(int*)(a-(int(b)&0x0000ffff));
b=(int*)(a+(int(b)&0x0000ffff));
}
算法做的最大改进就是采用位运算中的与运算“int(a)&0x0000ffff”,因为地址中高16位为段地址,后16位为位移地址,将它和0x0000ffff进行与运算后,段地址被屏蔽,只保留位移地址。这样就原始算法吻合,从而得到正确的结果。
此算法同样没有使用第三变量就完成了值的交换,与算术算法比较它显得不好理解,但是它有它的优点即在交换很大的数据类型时,它的执行速度比算术算法快。因为它交换的时地址,而变量值在内存中是没有移动过的。(以下称为地址算法)