柱状图中最大的矩形

题目：

　　给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

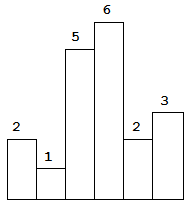
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]

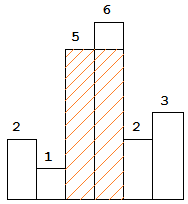
 图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

题解：

　　首先尝试暴力破解法，我们可以遍历每根柱子，以当前柱子 i 的高度作为矩形的高，那么矩形的宽度边界即为向左找到第一个高度小于当前柱体 i 的柱体，向右找到第一个高度小于当前柱体 i 的柱体。对于每个柱子我们都如上计算一遍以当前柱子作为高的矩形面积，最终比较出最大的矩形面积即可。暴力破解法效率较低，时间复杂度位O(N²)，暴力法代码如下：

　　

public int largestRectangleArea(int[] heights) {
        int area = 0, n = heights.length;
        // 遍历每个柱子，以当前柱子的高度作为矩形的高 h，
        // 从当前柱子向左右遍历，找到矩形的宽度 w。
        for (int i = 0; i < n; i++) {
            int w = 1, h = heights[i], j = i;
            while (--j >= 0 && heights[j] >= h) {
                w++;
            }
            j = i;
            while (++j < n && heights[j] >= h) {
                w++;
            }
            area = Math.max(area, w * h);
        }

        return area;
    }

　　暴力破解法进行了2次遍历，那我们能不能使用一次遍历就求出来呢？那就需要使用单调栈来实现了，依次遍历heights[]数组，比较当前柱子高度和栈顶元素(高度)的大小，若比栈顶元素小则栈顶元素出栈计算面积，否则出栈。代码如下：

 public int largestRectangleArea(int[] heights) {
        Stack<Integer> stack = new Stack<>();//单调递增栈
        int[] newHeights = new int[heights.length+1];
        for(int i=0;i<heights.length;i++){
            newHeights[i] = heights[i];
        }
        int maxArea = 0;
        newHeights[heights.length] = 0;//末尾添0，作为出栈栈的最后一个元素使用
        for(int i=0;i<newHeights.length;i++){
            //比较当前元素和栈顶元素的大小,计算栈顶元素的最大矩形面积
            while(!stack.isEmpty() && newHeights[i] < newHeights[stack.peek()]){
                int top = stack.pop();//下标idx
                //新栈顶的下标是stack.peek()
                int width = i,height = newHeights[top];
                if(!stack.isEmpty()){
                    width = i-stack.peek()-1;
                }
                maxArea = Math.max(maxArea,height * width);
            }
            stack.add(i);
        }

        return maxArea;
    }