HDU

  扫描线算法+线段树维护简介：

  像这种求面积的并集的题目，就适合用扫描线算法解决，具体来说就是这样

类似这种给出点的矩形的对角的点的坐标，然后求出所有矩形面积的交集的问题，可以采用扫描线算法解决。图如下，我们要求红色部分的面积：

 

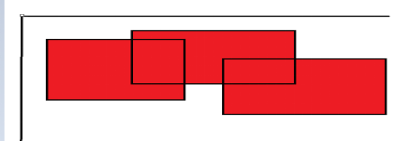
我们可以通过一条叫扫描线的东西解决问题。具体来说：

我们首先给自己一条线，这条可以我称之为标准线(棕色线表示)

 

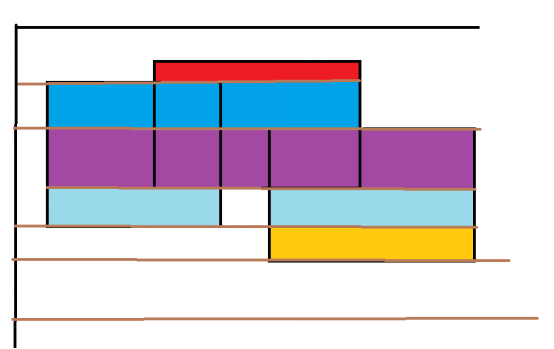
从上往下（从下往上也行）我们把每个矩形用一个四元组表示了l,r,h,f  也就是说，把一个矩形用上下两条边表示，l,r分别是x1,x2，而h则是y坐标，f代表这条线是顶边还是低边。

这样就把信息存储下来。

需要注意的一点是，由于线段树维护区间的时候，会存在区间过大的清空，因此我们需要对x坐标进行去重排序，从而达到把点进行离散化，但是这里我们需要注意的是，我们这里维护区间，而线段树是从维护点，进而维护区间的，因此我们可以这样，把区间的左下标表示为区间，比如[0-3]区间，我们可以转化为点0，代表0-1，1代表1-2，2代表2-3。这样我们再找左端点的时候，我们之间用坐标代替，而右端点，则需要查找到下标后，减一即可。

维护总的区间的和，用高度差乘以区间和，就是面积，每次维护，求出面积，就是如上图所示的样子，从下往上不断求出面积。

#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
inline int L(int r){return r<<1;};
inline int R(int r){return r<<1|1;};
inline int MID(int l,int r){return (l+r)>>1;};
const int maxx = 111;
struct segment{
  double l,r,h;
  int f;
}ss[maxx*2];
struct node{
  int l,r,cnt;
  double len;
}tree[maxx<<3];
double pos[maxx*2];
int nums;
bool cmp(segment p,segment q)
{
    return p.h<q.h;
}
void build(int root,int l,int r)
{
    tree[root].l=l;
    tree[root].r=r;
    tree[root].cnt=0;
    tree[root].len=0;
    if (l==r)
        return;
    int mid = MID(tree[root].l,tree[root].r);
    build(L(root),l,mid);
    build(R(root),mid+1,r);
}
void get_len(int root)
{
    if (tree[root].cnt)//不是0 代表已经被整段覆盖
        tree[root].len = pos[tree[root].r+1] - pos[tree[root].l];
    else if (tree[root].l == tree[root].r)//只是一个点
        tree[root].len = 0;
    else
        tree[root].len = tree[L(root)].len + tree[R(root)].len;
}
void update(int root,int l,int r,int val)
{
    if (tree[root].l == l && tree[root].r == r)
    {
        tree[root].cnt += val;
        get_len(root);
        return;
    }
    int mid = (tree[root].l + tree[root].r)>>1;
    if (r<=mid)
       update(L(root),l,r,val);
    else if (l > mid)
        update(R(root),l,r,val);
    else {
        update(L(root),l,mid,val);
        update(R(root),mid+1,r,val);
    }
   get_len(root);
}
int binary(double key,int low,int high)
{
   // cout<<key<<endl;
    int mid;
     while(low<=high)
     {
         mid = MID(low,high);
         if (pos[mid]==key)
             return mid;
         else if (key < pos[mid])
            high = mid-1;
         else
            low = mid+1;
     }
     return -1;
}
int main(){
  int Case = 0;
  int n;
  while(scanf("%d",&n)!=EOF && n)
  {
      nums=0;
      for (int i=0;i<n;i++){
        double x1,y1,x2,y2;
        scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
        //记录下边
        ss[nums].l = x1;
        ss[nums].r = x2;
        ss[nums].h = y1;
        ss[nums].f = 1;
        //记录上边
        ss[nums+1].l = x1;
        ss[nums+1].r = x2;
        ss[nums+1].h = y2;
        ss[nums+1].f = -1;
        //记录横坐标
        pos[nums] = x1;
        pos[nums+1] = x2;
        nums+=2;
      }
      sort(ss,ss+nums,cmp);
      sort(pos,pos+nums);
      int m = 1;
      for (int i=1;i<nums;i++)//离散去重
        if (pos[i]!=pos[i-1])
          pos[m++]=pos[i];
      memset(tree,0,sizeof(tree));
      build(1,0,m-1);//离散区间就是[0,m-1]
//      for (int i=0;i<=m*4+2;i++){
//        cout<<tree[i].l<<"-"<<tree[i].r<<endl;
//      }
      double ans = 0;
      for (int i=0;i<nums-1;i++)
      {
          int l = binary(ss[i].l,0,m-1);//二分找到s[i].l对应的离散化后的值
          int r = binary(ss[i].r,0,m-1)-1;//二分找到右端点但是由于需要把点转区间，因此减一
//          cout<<ss[i].l<<"->"<<l<<" ";
//          cout<<ss[i].r<<"->"<<r<<" ";
//          cout<<ss[i+1].h<<"-"<<ss[i].h<<endl;
          update(1,l,r,ss[i].f);//更新区间
          ans+=(ss[i+1].h-ss[i].h)*tree[1].len;
      }
        printf("Test case #%d
", ++Case);
        printf("Total explored area: %.2f

", ans);
  }
  return 0;
}