快速排序

介绍

通过一趟排序将要排序的数据分割为独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序。整个排序过程可以递归进行，以此达到整个数据变成有序序列。

过程

1.设置两个变量i、j，排序开始时：i=0，j=n-1;

2.以第一个数组元素作为关键数据，赋值给key，即key=A[0];

3.从j开始向前搜索（j--），找到第一个小于key的值A[j]，将他赋值给A[i];(直接覆盖即可，因为在上一步，被覆盖的值已经存到了合适的地方)

4.从i开始向后搜索（i++），找到第一个大于key的值A[i]，将他赋给A[j];

5.重复第3、4两步，直到i=j;

6.将k赋给A[i]。

代码

#include<iostream>
using namespace std;


void print(int a[], int n){
    for (int j = 0; j < n; j++){
        cout << a[j] << " ";
    }
    cout << endl;
}

int partition(int a[],int low,int high){
    int k = a[low];//基准元素
    while (low < high){
        while (a[high] >= k && low < high)
            --high;
        a[low] = a[high];
        while (a[low] <= k && low<high)
            ++low;
        a[high] = a[low];
    }
    a[low] = k;
    print(a, 10);
    return low;
}

void quikSort(int a[], int low, int high){
    if(low < high){
        int privotLoc = partition(a, low, high);
        quikSort(a, low, privotLoc - 1);
        quikSort(a, privotLoc + 1, high);
    }
}

int main(){
    int a[10] = { 3, 1, 5, 7, 2, 4, 11, 32, 5, 6 };
    quikSort(a, 0, 9);
    for (int i = 0; i < 10; i++){
        cout << a[i] << " ";
    }
    cout << endl;
    return 0;
}

效果

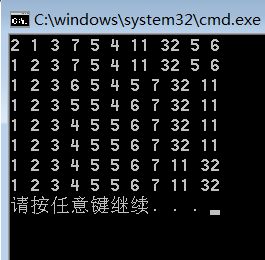
算法分析

时间复杂度：最坏O(n*n) 平均O(n*log(n))

空间复杂度: O(log(n))