1. 入门案例
1.1 分类的小例子--根据身高体重进行性别预测
%% 使用Libsvm进行分类的小例子
%{
一个班级里面有两个男生(男生1、男生2),两个女生(女生1、女生2),其中
男生1 身高:176cm 体重:70kg;
男生2 身高:180cm 体重:80kg;
女生1 身高:161cm 体重:45kg;
女生2 身高:163cm 体重:47kg;
如果我们将男生定义为1,女生定义为-1,并将上面的数据放入矩阵data中,
并在label中存入男女生类别标签(1、-1)
%}
train_data = [176 70;
180 80;
161 45;
163 47];
train_label = [1;1;-1;-1];
%{
这样上面的data矩阵就是一个属性矩阵,行数4代表有4个样本,列数2表示属性有两个,
label就是标签(1、-1表示有两个类别:男生、女生)。
%}
% 利用libsvm建立分类模型 此处options参数为默认值
model = svmtrain(train_label,train_data);
%{
此时该班级又转来一个新学生,其
身高190cm,体重85kg
我们想给出其标签(想知道其是男[1]还是女[-1])
由于其标签我们不知道,我们假设其标签为-1(也可以假设为1)
%}
test_data = [190 85];
test_label = -1;
[predict_label,accuracy,dec_value] = svmpredict(test_label,test_data,model);
predict_label
if 1 == predict_label
disp('==该生为男生');
end
if -1 == predict_label
disp('==该生为女生');
end
1.2 回归的小例子 y=x^2
利用训练集合已知的x,y来建立回归模型 model ,然后利用这个 model 去预测。
本例中的x相当于1.1中的属性矩阵 data ,y 相当于其中的 label ;相应的回归问题中 x 就是自变量,y 就是因变量。
%% 使用Libsvm进行回归的小例子
% 生成待回归的数据
x = (-1:0.1:1)';
y = -x.^2;
% 建模回归模型
model = svmtrain(y,x,'-s 3 -t 2 -c 2.2 -g 2.8 -p 0.01');
% 利用建立的模型看其在训练集合上的回归效果
[py,mse,dec_value] = svmpredict(y,x,model);
scrsz = get(0,'ScreenSize');
figure('Position',[scrsz(3)*1/4 scrsz(4)*1/6 scrsz(3)*4/5 scrsz(4)]*3/4);
plot(x,y,'o');
hold on;
plot(x,py,'r*');
legend('原始数据','回归数据');
grid on;
% 进行预测
testx = 1.1;
display('真实数据')
testy = -testx.^2
[ptesty,tmse,tdec_value] = svmpredict(testy,testx,model);
display('预测数据');
ptesty
2. 参数详解
2.1 主要函数
LIBSVM工具箱的主要函数为 svmtrain 和 svmpredict ,其调用格式为:
model = svmtrain(train_label,train_data,options);
[predict_label,accuracy/mse,dec_value] = svmpredict(test_label,test_data,model);
2.2 options 参数
options的参数设置可以按照 SVM 的类型和核函数所支持的参数进行任意组合。如果设置的参数在函数或 SVM 类型中没有也不会产生影响,程序不会接受该参数;如果应有的参数设置不正确,参数将采用默认值。主要有:
-s svm类型:SVM模型设置类型(默认值为0)
0:C - SVC
1:nu - SVC
2:one - class SVM
3: epsilon - SVR
4: nu - SVR
- t 核函数类型:核函数设置类型(默认值为2)
0:线性核函数 u'v
1:多项式核函数(r *u'v + coef0)^degree
2:RBF 核函数 exp( -r|u - v|^2)
3:sigmiod核函数 tanh(r * u'v + coef0)
- d degree:核函数中的 degree 参数设置(针对多项式核函数,默认值为3)
- g r(gama):核函数中的gama参数设置(针对多项式/sigmoid 核函数/RBF/,默认值为属性数目的倒数)
- r coef0:核函数中的coef0参数设置(针对多项式/sigmoid核函数,默认值为0)
- c cost:设置 C - SVC,epsilon - SVR 和 nu - SVR的参数(默认值为1)
- n nu:设置 nu-SVC ,one - class SVM 和 nu - SVR的参数
- p epsilon:设置 epsilon - SVR 中损失函数的值(默认值为0.1)
- m cachesize:设置 cache 内存大小,以 MB 为单位(默认值为100)
- e eps:设置允许的终止阈值(默认值为0.001)
- h shrinking:是否使用启发式,0或1(默认值为1)
- wi weight:设置第几类的参数 C 为 weight * C(对于 C - SVC 中的 C,默认值为1)
- v n:n - fold 交互检验模式,n为折数,必须大于等于2
2.3 分类模型 model 解析
测试数据使用 LIBSVM 工具箱自带的 heart_scale.mat 数据(共计270个样本,每个样本有13个属性)。测试代码如下:
clear; clc; close all; % 首先载入数据 load heart_scale; data = heart_scale_inst; label = heart_scale_label; % 建立分类模型 model = svmtrain(label,data,'-s 0 -t 2 -c 1.2 -g 2.8'); % 利用建立的模型看其在训练集合上的分类效果 [PredictLabel, accuracy, dec_values] = svmpredict(label,data, model);
accuracy
% 分类模型model解密
model
Parameters = model.Parameters
Label = model.Label
nr_class = model.nr_class
totalSV = model.totalSV
nSV = model.nSV
1)svmtrain 的输出 model:
model =
Parameters: [5x1 double]
nr_class: 2
totalSV: 259
rho: 0.0514
Label: [2x1 double]
sv_indices: [259x1 double]
ProbA: []
ProbB: []
nSV: [2x1 double]
sv_coef: [259x1 double]
SVs: [259x13 double]
2) model.Paramenters %参数表
Parameters =
0
2.0000
3.0000
2.8000
0
2) model.Paraments 参数意义从上到下依次为
-s svm类型:SVM模型设置类型(默认值为0) - t 核函数类型:核函数设置类型(默认值为2) - d degree:核函数中的 degree 参数设置(针对多项式核函数,默认值为3) - g r(gama):核函数中的gama参数设置(针对多项式/sigmoid 核函数/RBF/,默认值为属性数目的倒数) - r coef0:核函数中的coef0参数设置(针对多项式/sigmoid核函数,默认值为0)
3) model.Label model.nr_class
model.label 表示数据集中类别的标签都有什么
model.nr_class 表示数据集职工有多少个类别
4)model.totalSV model.nSV
model.total SV 代表总共的支持向量机的数目,这里一共259个。
model.nSV 代表每类样本的支持向量的数目,model.nSV 所代表的顺序是和 model.label 相对应。 标签为1的样本118个,标签为-1的样本 141 个。
5)model.sv_coef model.SVs model.rho
sv_coef: [259x1 double]
SVs: [259x13 double]
model.rho = 0.0514
sv_coef,承装的是259个支持向量在决策函数中的系数;
model.SVs 承装的是259个支持向量;
model.rho = 0.0514 是决策函数中的常数项的相反数。
6) accuracy
返回参数accuracy 从上到下的意义依次是:
分类准确率,分类问题中用到的参数指标;
平均平方误差( mean squared error,MSE),回归问题中用到的参数指标;
平方相关系数( squared correlation coefficient ,r2),回归问题中用到的参数指标。
![]()
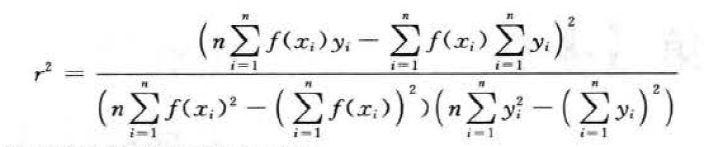
3. 决策函数
3.1 理论分析

3.2 代码实现
function plabel = DecisionFunction(x,model)
gamma = model.Parameters(4);
RBF = @(u,v)( exp(-gamma.*sum( (u-v).^2) ) );
len = length(model.sv_coef);
y = 0;
for i = 1:len
u = model.SVs(i,:);
y = y + model.sv_coef(i)*RBF(u,x);
end
b = -model.rho;
y = y + b;
if y >= 0
plabel = 1;
else
plabel = -1;
end
