一、写随笔的原因:排序比较常用,借此文介绍下排序常用的算法及实现,借此来MARK一下,方便以后的复习。(本人总是忘得比较快)
二、具体的内容:
1.插入排序
插入排序:在前面已经排好序的序列中找到合适的插入位置。
插入排序又可细分为:直接插入排序,二分法插入排序,希尔排序
(1)直接插入排序:简单来说,就是在每一步将一个待排序的数据,从后向前找到合适的位置插入,知道全部数据插入完,排序结束。(从第二个数开始,第一个数插入时没有其他数据,所以直接不用管)
Java代码实现如下:
/* 直接插入排序 */ public static int[] directInsertSort(int[] a) { // 实现从小到大排序 for (int i = 1; i < a.length; i++) { int temp = a[i]; // 存入当前待排序的数据 int j; for (j = i - 1; j >= 0; j--) { // 从后向前依次比较,插入到合适的位置 // (a[j]大于temp往后移动一位) if (temp < a[j]) { a[j + 1] = a[j]; } else { break; // a[j]不大于temp,则找到了合适的位置,直接退出循环 } } a[j + 1] = temp; // 把当前待排序的数据放入到找的位置(因为是从大到小所以放到j的后面) } return a; }
(2)二分法插入排序:思想都是插入排序的思想,只是在查找合适位置时是通过二分法来找位置的。
下面有个图可以很好的解释(盗图的):
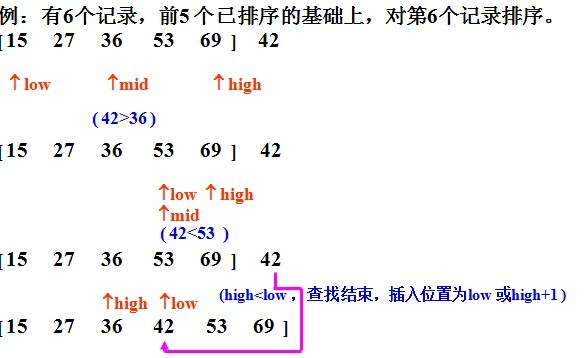
Java代码实现如下:
/* 二分法插入排序 */ public static void binaryInsertSort(int[] a) { for (int i = 0; i < a.length; i++) { int temp = a[i]; // 存入当前待排序的数据 int low = 0; //low的下标 int high = i - 1; //high的下标 int mid = 0; //mid下标 while (low <= high) { mid = (low + high) / 2; //算出mid位置 if (temp < a[mid]) { // temp小于mid位置的值,则继续与左边部分的位置使用二分 high = mid - 1; // 这时候的右下标需要修改为mid前一位 } else { // temp不小于mid位置的值,则继续与右边边部分的位置使用二分 low = mid + 1; // 这时候的右下标需要修改为mid后一位 } } // 找到位置后需要将原先位置上及后面的的数据向后平移一位,腾出位置插入 for (int j = i - 1; j >= low; j--) { a[j + 1] = a[j]; } if (low != i) { //low == i,则不需要变化,本来的位置就是正确的 a[low] = temp; } } }
(3)希尔排序:先取一个小于n的整数d1作为第一个增量,把文件的全部记录分成d1个组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2,直重复上述分组和排序操作;至di=1,即所有记录放进一个组中排序为止。
Java代码实现如下:
public static void shellSort(int[] a) { int d = a.length; // 不断缩小d,直至d=1 while (true) { d = d/2; for (int x = 0; x < d; x++) { for (int i = x + d; i < a.length; i = i + d) { int temp = a[i]; int j; // 相当于把直接插入排序的1变成了d for (j = i - d; j >= 0 && a[j] > temp; j = j - d) { a[j + d] = a[j]; } a[j + d] = temp; } } if (d == 1) { break; } } }
2.选择排序
选择排序:在剩余的待排序记录序列中找到最小数据。
选择排序又可细分为:直接选择排序,堆排序。
(1)直接选择排序:在要排序的一组数中,选出最小的一个数与第一个位置的数交换;然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。
如下图:

Java代码实现如下:
/* 直接选择排序 */ public static void directSelectSort(int[] a) { for (int i = 0; i < a.length; i++) { int min = a[i]; int n = i; // 最小数的索引 for (int j = i + 1; j < a.length; j++) { if (a[j] < min) { // 找出最小的 min = a[j]; n = j; } } // 最小的一个数与i位置的数交换 a[n] = a[i]; // n为最小的一个数的索引 a[i] = min; } }
(2)堆排序:堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。
首先简单了解下堆结构:堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:
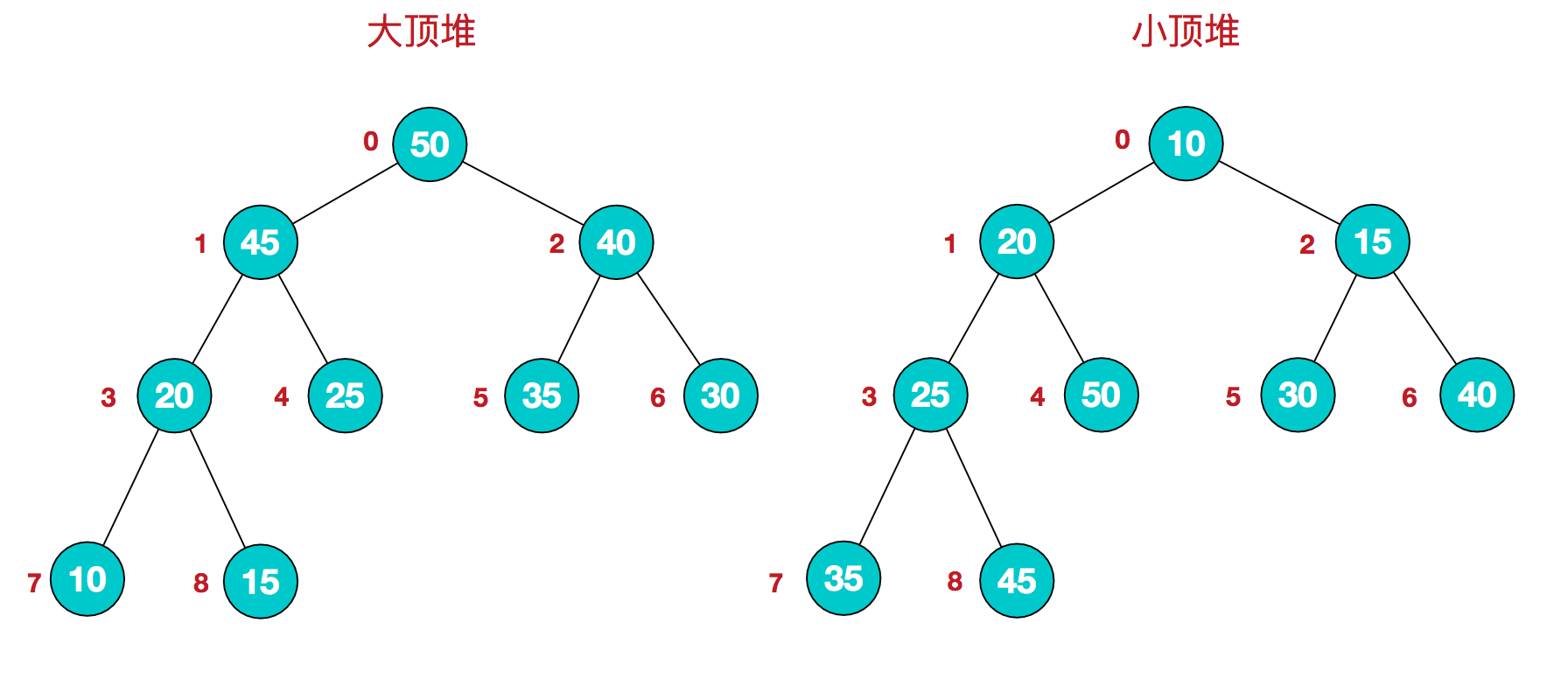
同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子:

我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
堆排序的基本思想是:
1.将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。
2.将其与末尾元素进行交换,此时末尾就为最大值。
3.然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
代码实现如下:
/* 堆排序 */ public static void heapSort(int[] a) { int arrayLength = a.length; // 循环建堆 for (int i = 0; i < arrayLength - 1; i++) { // 建堆 buildMaxHeap(a, arrayLength - 1 - i); // 交换堆顶和最后一个元素 swap(a, 0, arrayLength - 1 - i); } } // 对data数组从0到lastIndex建大顶堆 public static void buildMaxHeap(int[] data, int lastIndex) { // 从lastIndex处节点(最后一个节点)的父节点开始,即最后一个非叶子节点 for (int i = (lastIndex - 1) / 2; i >= 0; i--) { // k保存正在判断的节点 int k = i; // 如果当前k节点的子节点存在 while (k * 2 + 1 <= lastIndex) { // k节点的左子节点的索引 int biggerIndex = 2 * k + 1; // 如果biggerIndex小于lastIndex,即biggerIndex+1代表的k节点的右子节点存在 if (biggerIndex < lastIndex) { // 若果右子节点的值较大 if (data[biggerIndex] < data[biggerIndex + 1]) { // biggerIndex总是记录较大子节点的索引 biggerIndex++; } } // 如果k节点的值小于其较大的子节点的值 if (data[k] < data[biggerIndex]) { // 交换他们 swap(data, k, biggerIndex); // 将biggerIndex赋予k,开始while循环的下一次循环,重新保证k节点的值大于其左右子节点的值 k = biggerIndex; } else { break; } } } } // 交换 private static void swap(int[] data, int i, int j) { int tmp = data[i]; data[i] = data[j]; data[j] = tmp; }
三、总结:
本文主要是对插入排序和选择排序进行了讲解,并通过代码来实现。还有一些像交换排序,归并排序,基数排序等就作为第二部分内容在下次在写吧。