第六章 堆排序

堆

如图所示，堆是一个数组，它可以被看成是一棵完全二叉树。树上的每个结点对应数组中的一个元素。除了最底层外，该树是完全充满的，而且是从左向右填充。

表示堆的数组 A 包括两个属性：A.length 数组的大小，A.heapSize 元素个数。这里 0 ≤ A.heapSize ≤ A.length。

树的根结点是 A[1] ,这样给定一个结点的下标 i，我们很容易计算得到它的父结点 A[i/2] 、左孩子 A[2*i] 和右孩子 A[2*i+1] 。

堆可以分为两种形式：最大堆和最小堆。在这两种堆中，结点的值都要满足堆的性质，但一些细节定义有所差异。在最大堆中，除了根以外的所有结点都满足 A[i/2] ≥ A[i] ,也就是说某个结点的值至多与其父结点一样大。因此，堆中的最大元素存放在根结点中；并且，在任意子树中，该子树所包含的所有结点的值都不大于该子树根结点的值。最小堆的组织方式正好相反：除了根以外的所有结点都满足 A[i/2] ≤ A[i] ，最小堆中的最小元素存放在根结点中。

在堆排序算法中，我们使用的是最大堆。最小堆通常用于构造优先队列。

 

维护堆的性质

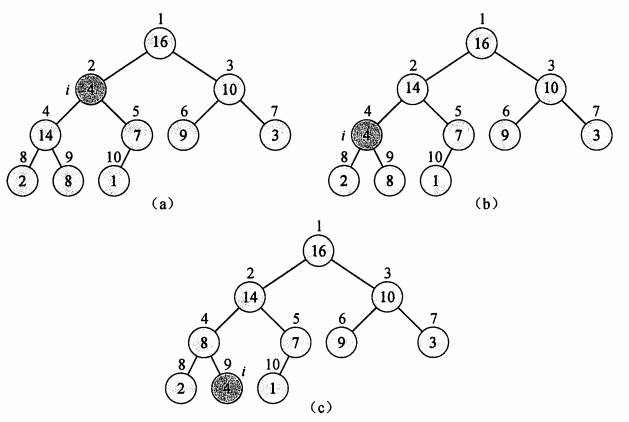
我们假设根结点的左右子树都是最大堆，但根结点 A[i] 可能小于其孩子，这就违背了最大堆的性质。MaxHeapify() 通过让 A[i] 在最大堆中“逐级下降”，从而使得以下标 i 为根结点的字数重新遵循最大堆的性质。

其做法是从 A[i]、A[2*i] 左孩子和 A[2*i+1] 右孩子中选出最大的，并将其下标存储在 maxI 中。如果 A[i] 是最大的，那么以 i 为根结点的子树已经是最大堆，程序结束。否则最大元素是 i 的某个孩子结点，需要交换 A[i] 和 A[maxI] 的值，从而使 i 及其孩子都满足最大堆的性质。在交换后，下标为 minI 的结点的值为原来的 A[i] ，以该结点为根的子树可能会违反最大堆的性质，因此，需要对该子树递归调用 MaxHeapify() 。

 代码实现

template<class T>
void MaxHeapify(T a[], int i, int heapSize) {
    int l = i * 2, r = i * 2 + 1;
    int maxI = i;
    if (l <= heapSize) {
        maxI = a[i] >= a[l] ? i : l;
    }
    if (r <= heapSize) {
        maxI = a[maxI] >= a[r] ? maxI : r;
    }
    if (maxI != i) {
        swap(a[i], a[maxI]);
        MaxHeapify(a, maxI, heapSize);
    }
}

建堆

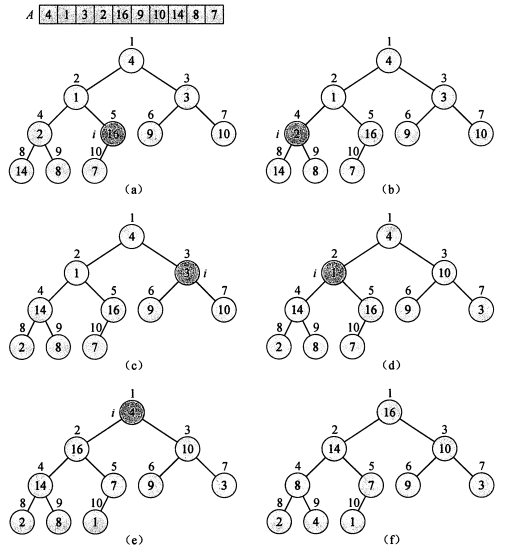
子数组 A[(n/2)+1...n] 中的元素都是树的叶结点，可看作只包含一个元素的堆，不做处理。剩余元素，我们可以采用自底向上的方法，利用 MaxHeapify() 过程把一个大小为 n 的数组 A[1...n] 转换为最大堆。

 代码实现

template<class T>
void BuildMaxHeap(T a[], int heapSize) {
    for (int i = heapSize / 2; i >= 1; i--) {
        MaxHeapify(a, i, heapSize);
    }
}

堆排序算法

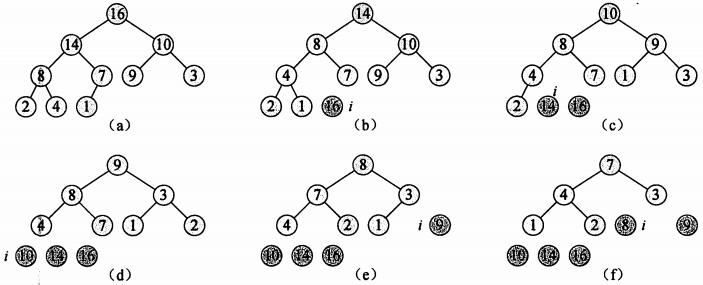
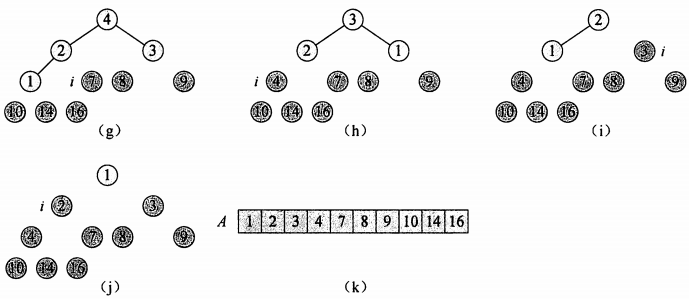
初始时，堆排序算法利用 BuildMaxHeap() 将输入数组 A[1...n] 建成最大堆，因为数组中的最大元素总在根结点 A[1] 中，通过把它与 A[n] 进行交换，我们可以让该元素放到正确位置。这时候，如果我们从堆中去掉结点 n（A.heapSize --）,剩余结点中，原来根的左右子树仍然是最大堆，而新的根结点可能会违背最大堆的性质，我们要做的是调用 MaxHeapify(A，1)，从而构造一个新的最大堆。堆排序算法会不断重复这个过程，直到堆的大小为 1。

 

代码实现

template<class T>
void HeapSort(T a[], int heapSize) {
    BuildMaxHeap(a, heapSize);
    while (heapSize != 1) {
        swap(a[1], a[heapSize]);
        heapSize--;
        MaxHeapify(a, 1, heapSize);
    }
}

堆中插入元素

增加一个叶结点用来放置新元素，新元素不断与其父结点进行比较，若新元素较大，则与其父结点进行交换。不断重复这个过程，直到当前元素小于其父结点时停止。

代码实现

template<class T>
void Insert(T a[], T x,int heapSize) {
    a[++heapSize] = x;
    int i = heapSize;
    while (i > 1 && a[i / 2] < a[i]) {
        swap(a[i], a[i / 2]);
        i = i / 2;
    }
}