OI 学习笔记 (2)：线段树

前言

本文浅谈了线段树的几种模型和一些例题。

参考资料：

• qzhwlzy的博客

概况

线段树，是一类可以在对数复杂度内处理区间型问题的数据结构。

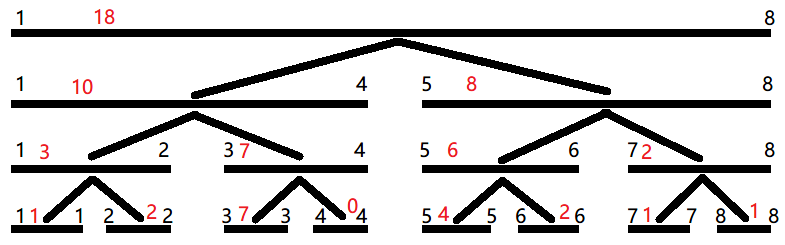
这是一张线段树的图。容易发现，线段树是一棵二叉树，每个节点保存了这个节点管理的区间 \(l,r\)（黑色数字）这个区间的 \(\operatorname{sum}\)（红色数字）（也可以是 \(\max,\min\) 等等）。

构造

在图中，我们发现了线段树的一些特征：一个节点的两个儿子节点分别管理这个节点的一半，一个节点的 \(\operatorname{sum}\) 值等于两个儿子节点的 \(\operatorname{sum}\) 值。通过这两个特征，就可以通过递归的方式构造一棵线段树（应该都知道二叉树的简便构造方法吧）。

CI N = 1e5, N4 = 4e5; int sum[N4 + 5], l[N4 + 5], r[N4 + 5], arr[N + 5]; // 线段树需要开四倍大小
void pushup (int root) {sum[root] = sum[root << 1] + sum[root << 1 | 1];} // 线段树子节点向父亲节点更新
void build (int root, int L, int R) {
	l[root] = L; r[root] = R;
	if (L == R) {sum[root] = arr[L]; return ;} // 叶子节点
	int mid = (L + R) >> 1; build (root << 1, L, mid); build (root << 1 | 1, mid + 1, R);
	pushup (root); // 向上更新
}

区间查询+单点修改

区间查询

还是上面那棵线段树，如果我们需要查询区间 \([1,7]\) 的和，一种做法当然是从 \([1,1]\) 加到 \([7,7]\)（那你写线段树干嘛）。但是我们发现，从 \([1,1]\) 到 \([4,4]\) 的和就是 \([1,4]\) 的 \(\operatorname{sum}\) 值。所以 \([1,7]\) 的和就等于 \([1,4],[5,6],[7,7]\) 的和。但是怎么判断查询区间可以分成几个小区间呢？考虑分类，我们从根节点向下递归（因为从上向下递归的，可以保证分割的区间数最少）：如果当前区间包含在查询区间内，那么直接返回该节点 \(\operatorname{sum}\) 值；如果查询区间与当前区间的左儿子有交集，向左儿子递归；如果右儿子有交集，向右儿子递归。

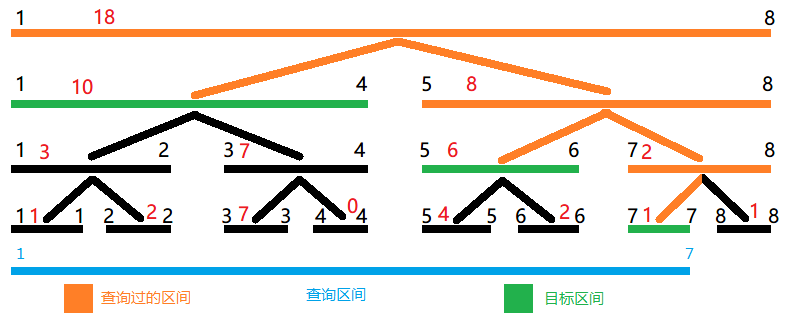
int Sum (int root, int L, int R) {
	if (l[root] >= L && r[root] <= R) return sum[root]; // 查询区间包含当前区间 
	if (r[root] < L || l[root] > R) return 0; // 无交集 
	int mid = (l[root] + r[root]) >> 1, s = 0;
	if (L <= mid) s += Sum (root << 1, L, R); // 左儿子有交集 
	if (R > mid) s += Sum (root << 1 | 1, L, R); // 右儿子有交集 
	return s;
}

单点修改

（比区间查询简单多了）只需要找到对应的叶子节点，在递归返回的时候向上更新就好了。

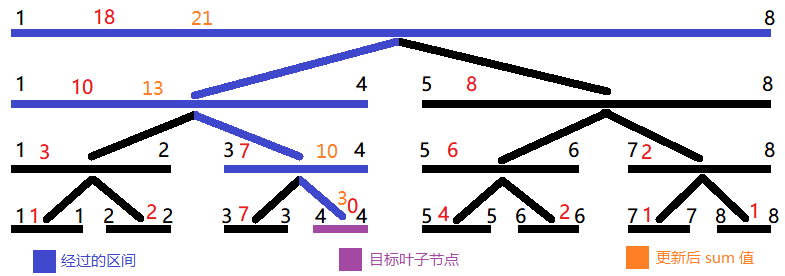
void change (int root, int x, int k) {
	if (l[root] == r[root]) {sum[root] += k; return ;} // 到达叶子节点
	if (l[root] > x || r[root] < x) return ;
	int mid = (l[root] + r[root]) >> 1;
	if (x <= mid) change (root << 1, x, k);
	else if (x > mid) change (root << 1 | 1, x, k);
	pushup (root); // 向上更新
}

单点查询+区间修改

考虑换一种实现方式，我们构造一棵 \(\operatorname{sum}\) 值全为 \(0\) 的线段树。区间修改时把包含的区间加上 \(k\) 的标记，单点查询时把沿路的标记加起来，再加上这个点原本的值即可。