• 二分图与最大匹配

    二分图常识

    定义

    二分图，又称二部图，英文名叫 Bipartite graph。
    二分图是什么？节点由两个集合组成，且两个集合内部没有边的图。
    换言之，存在一种方案，将节点划分成满足以上性质的两个集合。

    选自OI Wiki [1]

    通俗一点就是一个图如果能分成两部分，且两部分内部没有边，则这是一张二分图。

    充要条件

    二分图中没有奇数环。如果有奇数环，则必然有一个集合里两点相连，否则不能成为环。

    判定

    通过充要条件，我们只需要找奇数环就好了。不过还有一种判定方法：使用两种颜色，将节点进行染色，把一条边上的点染成不同的颜色，如果发现了冲突，则不是二分图。

    关于二分图的匹配

    给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。

    节选自百度百科 [2]

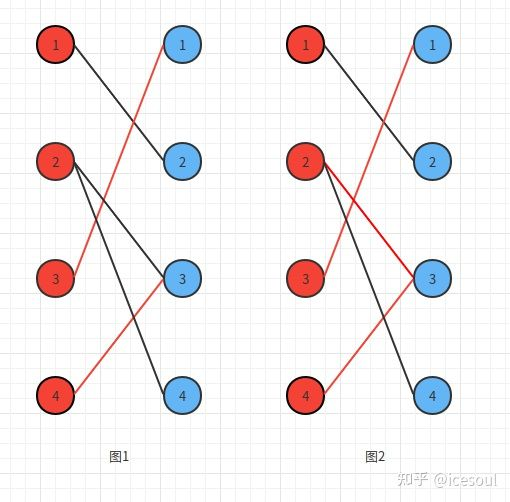
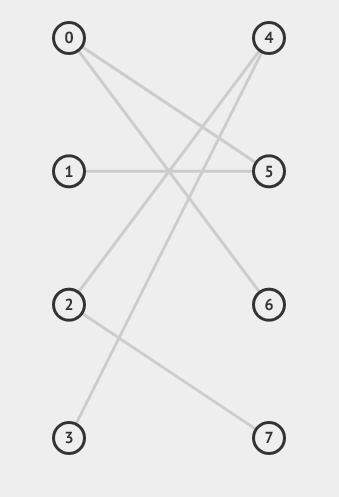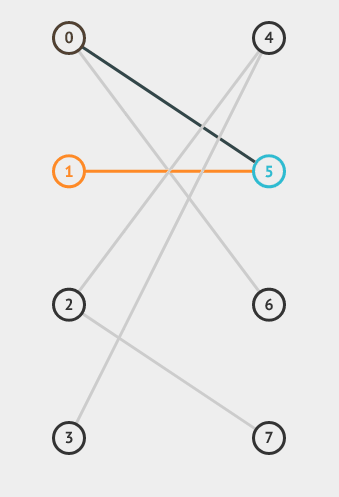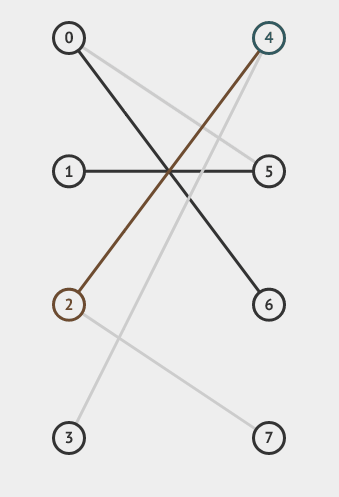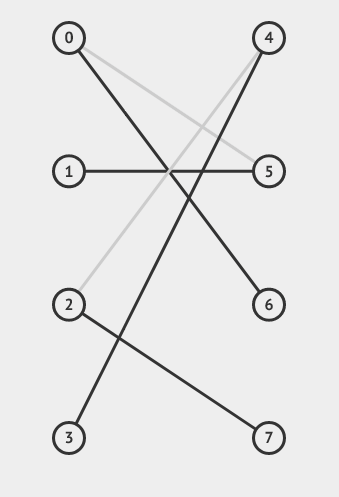
    如下图，图1是一个匹配（红色边为已匹配，黑色边为未匹配），而图2显然不是一个匹配。

    image

    二分图最大匹配

    指在所有匹配的方案中，匹配边数最多的一种匹配。特殊的，如果所有点均被匹配，则这种匹配方案为完美匹配。

    匈牙利算法

    增广路

    若P是图G中一条连通两个未匹配顶点的路径，并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径

    节选自百度百科 [3]

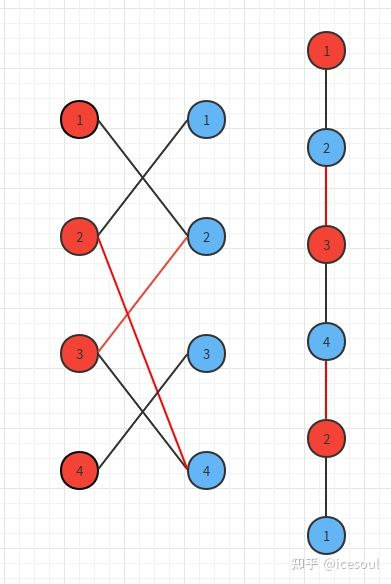
    如下图，在下图的匹配中， (1 o 2 o 3 o 4 o 2 o 1) 为一条增广路（注意，增广路的第一条边和最后一条边一定是未匹配的）。

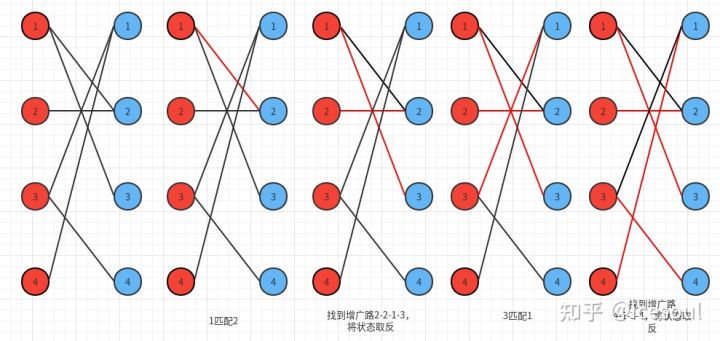
    image

    知道了增广路的含义，就可以求最大匹配了。如果在二分图中找到了一条增广路，由于一条增广路上未匹配的边肯定比匹配的边多1，所以如果将增广路上未匹配的边改为匹配的边，匹配的边改成未匹配的边，那么既不破坏匹配的定义，又能使匹配的边数+1。匈牙利算法便是如此：在二分图中寻找增广路，并修改边的匹配情况，如果没有增广路了，那么这张图就达到最大匹配了，如下图的模拟过程：

    image

    还有一个动图模拟：

    image

    寻找增广路，可以用dfs。

    P3386 【模板】二分图最大匹配

    点击查看代码 
    #include <bits/stdc++.h>
#define Tp template <typename Ty>
#define I inline
#define LL long long
#define Con const
#define Reg register
#define CI Con int
#define CLL Con LL
#define RI Reg int
#define RLL Reg LL
#define W while
#define max(x, y) ((x) > (y) ? (x) : (y))
#define min(x, y) ((x) < (y) ? (x) : (y))
#define Gmax(x, y) (x < (y) && (x = (y)))
#define Gmin(x, y) (x > (y) && (x = (y)))
struct FastIO
{
    Tp FastIO &operator>>(Ty &in)
    {
        in = 0;
        char ch = getchar();
        bool flag = 0;
        for (; !isdigit(ch); ch = getchar())
            (ch == '-' && (flag = 1));
        for (; isdigit(ch); ch = getchar())
            in = (in * 10) + (ch ^ 48);
        in = (flag ? -in : in);
        return *this;
    }
} fin;
CI MaxN = 5e2 + 100;
int n, m, e, eg[MaxN][MaxN]; // 邻接矩阵存图
int use[MaxN], vis[MaxN];
bool search(int now) // 寻找增广路
{
    for (int i = 1; i <= m; ++i)
    {
        if (eg[now][i] && !vis[i]) // 如果有边且这个边没有被走过
        {
            vis[i] = 1;
            if (!use[i] || search(use[i]))
            // 如果这个点没有被用过或者这个点可以给他提供位置（即有增广路）
            {
                use[i] = now;
                return 1;
            }
        }
    }
    return 0;
}
int get()
{
    fin >> n >> m >> e;
    for (int i = 1; i <= e; ++i)
    {
        int u, v;
        fin >> u >> v;
        eg[u][v] = 1; // 建边
    }
    int ans = 0;
    for (int i = 1; i <= n; ++i)
    {
        memset(vis, 0, sizeof(vis));
        ans += search(i); // 如果有增广路就将最大匹配+1（因为找到增广路匹配的边就会多1）
    }
    printf("%d
", ans);
    return 0;
}
int main() { return get() && 0; }

    最大流

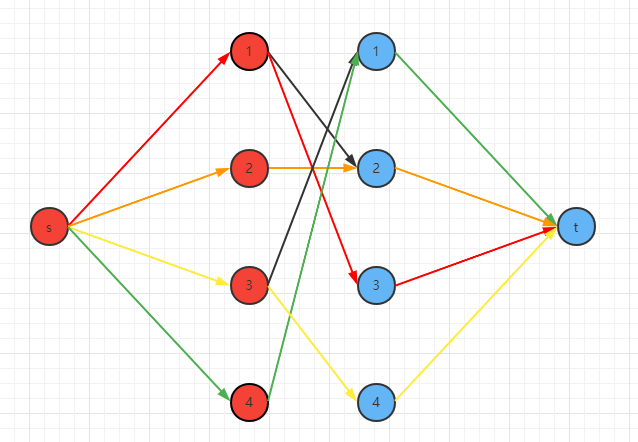
    没错，网络流[4]最大流也能处理二分图的最大匹配，新建一个源点s和一个汇点t，将s与一个点集的所有点连边，将t与另一个点集的所有点连边，所有边的流量均为1，然后跑最大流。为什么这样可以实现呢？因为最大流的目的是使源点到汇点的流量最多，将边的流量设为1，就刚好满足最大匹配的要求，最大流的算法，用EK或者Dinic都行。

    image

    点击查看代码 
    #include <bits/stdc++.h>
#define Tp template <typename Ty>
#define I inline
#define LL long long
#define Con const
#define Reg register
#define CI Con int
#define CLL Con LL
#define RI Reg int
#define RLL Reg LL
#define W while
#define max(x, y) ((x) > (y) ? (x) : (y))
#define min(x, y) ((x) < (y) ? (x) : (y))
#define Gmax(x, y) (x < (y) && (x = (y)))
#define Gmin(x, y) (x > (y) && (x = (y)))
struct FastIO
{
    Tp FastIO &operator>>(Ty &in)
    {
        in = 0;
        char ch = getchar();
        bool flag = 0;
        for (; !isdigit(ch); ch = getchar())
            (ch == '-' && (flag = 1));
        for (; isdigit(ch); ch = getchar())
            in = (in * 10) + (ch ^ 48);
        in = (flag ? -in : in);
        return *this;
    }
} fin;
CI MaxN = 510, MaxM = 1e5 + 100;
int nxt[MaxM << 1], to[MaxM << 1], w[MaxM << 1], pre[MaxM << 1], edge[MaxM << 1], head[MaxN], cnt = 1, s, t, n, m, e;
bool vis[MaxN];
void add(int u, int v, int ww)
{
    ++cnt;
    w[cnt] = ww;
    to[cnt] = v;
    nxt[cnt] = head[u];
    head[u] = cnt;
}
bool bfs() // 寻找增广路
{
    std ::queue<int> q;
    memset(vis, 0, sizeof(vis));
    vis[s] = 1;
    q.push(s);
    W(!q.empty())
    {
        int p = q.front();
        q.pop();
        for (int i = head[p]; i; i = nxt[i])
            if (!vis[to[i]] && w[i])
            {
                vis[to[i]] = 1;
                pre[to[i]] = p;
                edge[to[i]] = i;
                if (to[i] == t)
                    return 1;
                q.push(to[i]);
            }
    }
    return 0;
}
void dfs() // EK算法
{
    LL ans = 0;
    W(bfs())
    {
        int minn = 0x7fffffff;
        for (int i = t; i != s; i = pre[i])
            Gmin(minn, w[edge[i]]);
        for (int i = t; i != s; i = pre[i])
            w[edge[i]] -= minn, w[edge[i] ^ 1] += minn;
        ans += minn;
    }
    printf("%lld
", ans);
}
int get()
{
    fin >> n >> m >> e;
    for (int i = 1; i <= e; ++i)
    {
        int u, v;
        fin >> u >> v;
        v += n;
        add(u, v, 1);
        add(v, u, 0);
    }
    s = n + m + 1;
    t = n + m + 2;
    for (int i = 1; i <= n; ++i) // 建边
    {
        add(s, i, 1);
        add(i, s, 0);
    }
    for (int i = 1; i <= m; ++i) // 建边
    {
        add(i + n, t, 1);
        add(t, i + n, 0);
    }
    dfs();
    return 0;
}
int main() { return get() && 0; }

    二分图最大权匹配

    二分图的最大权匹配是指二分图中边权和最大的匹配。

    KM算法

    KM，全名Kuhn-Munkres，是求解二分图最大权完美匹配的一种算法。

    考虑到二分图中两个集合中的点并不总是相同，为了能应用 KM 算法解决二分图的最大权匹配，需要先作如下处理：将两个集合中点数比较少的补点，使得两边点数相同，再将不存在的边权重设为0，这种情况下，问题就转换成求最大权完美匹配问题，从而能应用 KM 算法求解。

    节选自OI Wiki [5]

    如何求最大权完美匹配？需要引入几个概念：

    可行顶标：就是给每个点分配一个点权 (a_i)，且对于每一条边 ((u,v))，需要满足 (a_u+a_v ge w(u,v))

    相等边：当一条边满足 (w(u,v)=a_u+a_v)，这条边叫做相等边

    相等子图：由一些点和相等边组成的子图叫做相等子图

    知道了这些概念，二分图最大匹配就很简单了。只需要判断，如果一个二分图的相等子图是它的一个完美匹配，那么这个相等子图就是最大权完美匹配。

    那如何确定顶标的值呢。假设二分图左边点的顶标为 (lx_i)，右边点的顶标为 (ly_i)。因为要满足顶标的定义，那就设 (lx_i)为0， (设ly_i)为与他相连的边，边权的最大值。

    调整顶标的过程，其实就是将相等子图扩大的过程，也就是使更多的边成为相等边。假设一条边 ((i,j))， (i) 不在最大匹配内， (j) 在最大匹配内。如果要使这条边加入最大匹配，则顶标和要减少 (d=lx_i+ly_j-w(i,j)) ，且 (d) 要尽量小。

    因为点 jj 肯定还在最大匹配中，所以减完以后肯定会影响到其他边。于是草率一点，对于已将二分图最大匹配中的所有点，将 (lx_i+d) 或将 (ly_i-d) ，这样就解决了。

    显然，这样的复杂度为 (O(n^4)) ，考虑到每次都重新找 (d) 太慢了。那就新建一个数组 (slack_i) ，且满足 (slack_j=min(lx_i+ly_i-w(i,j))) ，查询时直接调用即可。至于修改，在查找增广路时修改即可。

    如果看不懂，可以结合下面的模拟过程来理解：

    首先，初始化顶标：

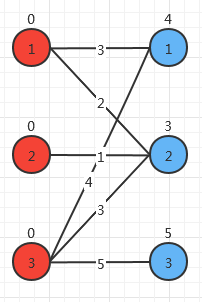
    image

    对右边的1匹配，匹配到3。

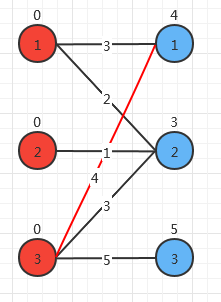
    image

    对右边的2匹配，匹配到3，由于3被匹配，将右边的1，2的顶标-（3+0-2）=1，左边的3的顶标 +（3+0-2）=1:

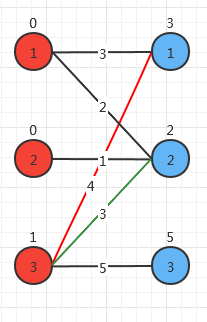
    image

    这样，右边的2就可以找到左边的1。

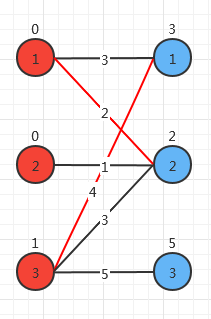
    image

    对右边的3匹配，它只能匹配左边的3，所以将右边的3的顶标-（5+1-5）=1

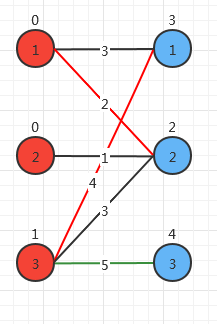
    image

    右边的3找到左边的3，左边的3找到右边的1，右边的1找到左边的1，左边的1找到右边的2，右边的2又找到左边的2，找到了一条增广路，将左边的1,3的顶标+1，右边1,2,3的顶标-1。

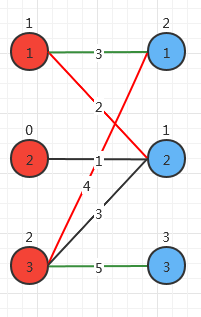
    image

    发现右边的2和左边的2可以匹配，完成。

    image

    P6577 【模板】二分图最大权完美匹配

    点击查看代码 
    #include <bits/stdc++.h>
#define Tp template <typename Ty>
#define I inline
#define LL long long
#define Con const
#define Reg register
#define CI Con int
#define CLL Con LL
#define RI Reg int
#define RLL Reg LL
#define W while
#define max(x, y) ((x) > (y) ? (x) : (y))
#define min(x, y) ((x) < (y) ? (x) : (y))
#define Gmax(x, y) (x < (y) && (x = (y)))
#define Gmin(x, y) (x > (y) && (x = (y)))
struct FastIO
{
	Tp FastIO &operator>>(Ty &in)
	{
		in = 0;
		char ch = getchar();
		bool flag = 0;
		for (; !isdigit(ch); ch = getchar())
			(ch == '-' && (flag = 1));
		for (; isdigit(ch); ch = getchar())
			in = (in * 10) + (ch ^ 48);
		in = (flag ? -in : in);
		return *this;
	}
} fin;
CI MaxN = 510;
CLL inf = 1e18;
LL n, m, w[MaxN][MaxN], lx[MaxN], ly[MaxN], link[MaxN], slack[MaxN];
bool visx[MaxN], visy[MaxN];
bool dfs(LL x) // 寻找增广路
{
	visy[x] = 1; // 遍历标记
	for (int i = 1; i <= n; ++i)
	{
		if (visx[i])
			continue;
		LL t = lx[i] + ly[x] - w[x][i]; // 题解中的d
		if (t == 0)
		{
			visx[i] = 1;
			if (link[i] == 0 || dfs(link[i]))
			{
				link[i] = x; // 和二分图最大匹配一样
				return 1;
			}
		}
		else if (slack[i] > t) // 更新slack
			slack[i] = t;
	}
	return 0;
}
LL KM()
{
	memset(lx, 0, sizeof(lx)); // 初始化
	memset(ly, 0, sizeof(ly));
	memset(link, 0, sizeof(link));
	for (int i = 1; i <= n; ++i)
	{
		ly[i] = w[i][1];
		for (int j = 2; j <= n; ++j)
			Gmax(ly[i], w[i][j]); // 初始化顶标
	}
	for (int i = 1; i <= n; ++i)
	{
		for (int j = 1; j <= n; ++j)
			slack[j] = inf;
		W(1)
		{
			memset(visx, 0, sizeof(visx));
			memset(visy, 0, sizeof(visy));
			if (dfs(i))
				break;
			LL d = inf;
			for (int k = 1; k <= n; ++k)
				if (!visx[k] && d > slack[k]) // 计算d
					d = slack[k];
			for (int k = 1; k <= n; ++k)
			{ // 核心部分，更新顶标
				if (visy[k])
					ly[k] -= d;
				if (visx[k])
					lx[k] += d;
				else
					slack[k] -= d;
			}
		}
	}
	LL ans = 0;
	for (int i = 1; i <= n; ++i)
		ans += w[link[i]][i]; // 统计答案
	return ans;
}
int get()
{
	fin >> n >> m;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= n; ++j)
			w[i][j] = -inf;
	for (int i = 1, u, v, ww; i <= m; ++i)
	{
		fin >> u >> v >> ww;
		w[u][v] = ww;
	}
	printf("%lld
", KM());
	for (int i = 1; i <= n; ++i)
		printf("%d ", link[i]);
	printf("
");
	return 0;
}
int main() { return get() && 0; }

    但是这份代码只有55分，因为在寻找增广路的时候，时间复杂度可能卡到 (O(n^2)) ，所以只要把 dfs 改成 bfs ，就能解决了（正常出题人不会卡dfs版的KM）。

    点击查看代码 
    #include <bits/stdc++.h>
#define Tp template <typename Ty>
#define I inline
#define LL long long
#define Con const
#define Reg register
#define CI Con int
#define CLL Con LL
#define RI Reg int
#define RLL Reg LL
#define W while
#define max(x, y) ((x) > (y) ? (x) : (y))
#define min(x, y) ((x) < (y) ? (x) : (y))
#define Gmax(x, y) (x < (y) && (x = (y)))
#define Gmin(x, y) (x > (y) && (x = (y)))
struct FastIO
{
	Tp FastIO &operator>>(Ty &in)
	{
		in = 0;
		char ch = getchar();
		bool flag = 0;
		for (; !isdigit(ch); ch = getchar())
			(ch == '-' && (flag = 1));
		for (; isdigit(ch); ch = getchar())
			in = (in * 10) + (ch ^ 48);
		in = (flag ? -in : in);
		return *this;
	}
} fin;
CI MaxN = 510;
CLL inf = 1e18;
LL n, m, w[MaxN][MaxN], lx[MaxN], ly[MaxN], link[MaxN], slack[MaxN], pre[MaxN];
bool visx[MaxN], visy[MaxN];
void bfs(LL u)
{
	LL x, y = 0, yy = 0, delta;
	memset(pre, 0, sizeof(pre));
	for (int i = 1; i <= n; ++i)
		slack[i] = inf;
	link[y] = u;
	W(1)
	{
		x = link[y];
		delta = inf;
		visy[y] = 1;
		for (int i = 1; i <= n; ++i)
		{
			if (visy[i])
				continue;
			if (slack[i] > lx[x] + ly[i] - w[x][i])
				slack[i] = lx[x] + ly[i] - w[x][i], pre[i] = y;
			if (slack[i] < delta)
				delta = slack[i], yy = i;
		}
		for (int i = 0; i <= n; ++i)
		{
			if (visy[i])
				lx[link[i]] -= delta, ly[i] += delta;
			else
				slack[i] -= delta;
		}
		y = yy;
		if (link[y] == -1)
			break;
	}
	W (y)
	{
		link[y] = link[pre[y]];
		y = pre[y];
	}
}
LL KM()
{
	memset(link, -1, sizeof(link));
	memset(lx, 0, sizeof(lx));
	memset(ly, 0, sizeof(ly));
	for (int i = 1; i <= n; ++i)
		memset(visy, 0, sizeof(visy)), bfs(i);
	LL ans = 0;
	for (int i = 1; i <= n; ++i)
		if (link[i] != -1)
			ans += w[link[i]][i];
	return ans;
}
int get()
{
	fin >> n >> m;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= n; ++j)
			w[i][j] = -inf;
	for (int i = 1, u, v, ww; i <= m; ++i)
	{
		fin >> u >> v >> ww;
		w[u][v] = ww;
	}
	printf("%lld
", KM());
	for (int i = 1; i <= n; ++i)
		printf("%d ", link[i]);
	printf("
");
	return 0;
}
int main() { return get() && 0; }

    参考

    1. https://oi-wiki.org/graph/bi-graph/ ↩︎

    2. https://baike.baidu.com/item/二分图匹配/9089174?fr=aladdin ↩︎

    3. https://baike.baidu.com/item/增广路/1332250?fr=aladdin ↩︎

    4. https://baike.baidu.com/item/网络流/2987528?fr=aladdin ↩︎

    5. https://oi-wiki.org//graph/graph-matching/bigraph-weight-match/#hungarian-algorithmkuhn-munkres-algorithm ↩︎
  • 相关阅读:
    tomcat-jvm参数优化
    k8s集群命令用法
    Zabbix-配置QQ邮箱报警通知
    zabbix监控实现原理
    adb无线调试安卓
    tiddlywiki安装和入门
    python处理excel和word脚本笔记
    路由和交换机调试笔记
    linux常用命令
    进程和线程的代码实现
  • 原文地址：https://www.cnblogs.com/binghun/p/15193582.html
Copyright © 2020-2023  润新知