本文主要是对《信息安全技术》的DES算法实验作业的一些总结,不会着重地介绍算法原理,而会在算法实现过程中给出自己的理解(因为有些部分我也不知道正确与否,如有错误请指教)。文章中出现的原理介绍和配图,均参考自其它博客,相关链接将在文中给出。
另外,文中的代码都是根据内容截取的,若想查看完整代码,请参考 DES - github
一、DES算法简介(参考自DES算法实例详解)
DES(Data Encryption Standard)是一种用于电子数据加密的对称密钥块加密算法。它以64bit一组的明文(Input)作为算法的输入,通过一系列复杂的操作,输出同样64bit长度的密文(Output)。DES 同样采用64位密钥(Key),但由于每8bit中的最后1位用于奇偶校验,实际有效密钥长度为56bit(Tips:输入的Key依然是64bit,只是在映射时不对每个字节最后1位进行处理,所以变为了56bit)。
DES 使用加密密钥定义变换过程,因此算法认为只有持有加密所用的密钥的用户才能解密密文。DES的两个重要的安全特性是混淆和扩散。其中混淆是指通过密码算法使明文和密文以及密钥的关系非常复杂,无法从数学上描述或者统计。扩散是指明文和密钥中的每一位信息的变动,都会影响到密文中许多位信息的变动,从而隐藏统计上的特性,增加密码的安全。
上图是DES算法的流程图。左侧是算法的工作流程,可以看到:
(1)用64bit的密钥Key产生16个48bit的子密钥;
(2)对输入的64bit明文先进行了Initial Permutation(IP初始置换);
(3)将64bit分为左右两部分(各32bit),用16个子密钥辅助进行16轮的F变换;
(4)两部分合成为64bit,进行Final Permutation(FP最终置换/逆置换)形成密文输出
而我们可以看到,在(3)中的16轮变换中,都需要右侧图中由密钥(Key)产生的子密钥(Sub-Key #i)。因此,我们可以首先来处理初始置换部分和子密钥算法部分。
二、算法准备
2.1、数据结构
首先要确定的是数据结构,即如何保存算法过程中出现的二进制、八进制和字符串数据?显然的,在C++中,我们可以全都用string来进行存储,但是对于算法中经常进行的异或操作,就不是很方便了。
对于整数和单个字符,我们的数据范围不会很大,不论是字符还是数字使用unsigned char即可。因此先定义类型:
typedef unsigned char Byte;对于其它数据,我们使用string类型来保存这些数据。但是需要进行位操作时,我们就将这些数据转换为C++中bitset类型来保存。关于bitset类型的介绍可以参考博客C++ bitset 用法,这里不再赘述。但是有一点需要特别特别注意,使用索引index来获取数据时,是从低位开始的。也就是说,若有bitset<4> bs("0001"),那么bs[0]==1,bs[3]==0。
2.2、置换操作
在算法过程中,我们经常可以看到对位数据进行置换操作。那么到底置换操作是怎么进行的呢?
// 要特别注意的是bitset的index由0->size-1是从 低位->高位,即右边->左边
// 置换操作模板函数
template <typename Input, typename Output>
void DES_Permutation(const Input& input, Output& output
, const Byte Table[], const Byte tableSize)
{
for(Byte i = 0; i < tableSize; ++i)
output[tableSize - i - 1] = input[input.size() - Table[i]];
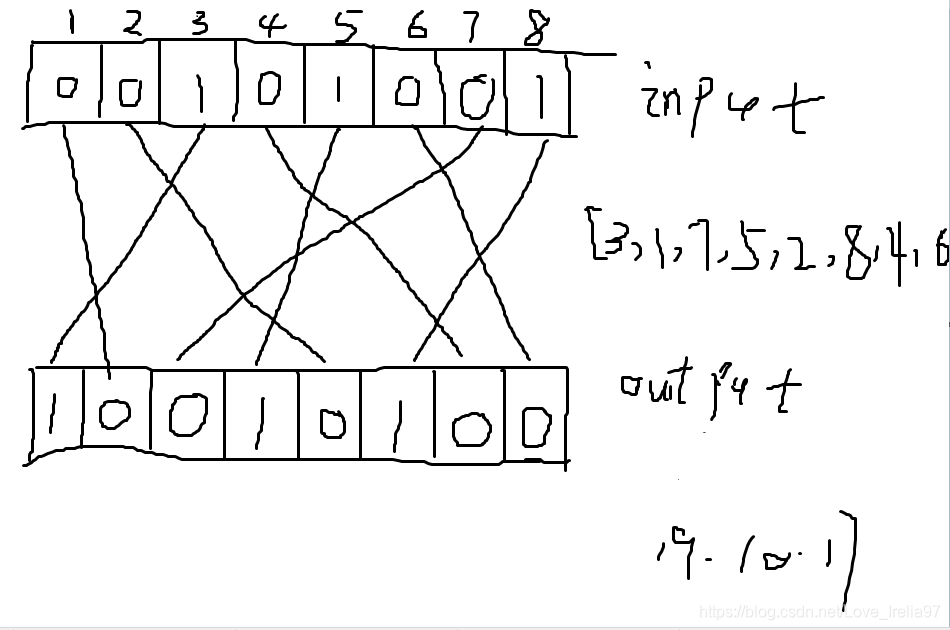
}举一个简单的例子,bitset<8> input("00101001"),input.size()为8。现在有置换数组Table {3, 1, 7, 5, 2, 8, 4, 6},tableSize为8。那么现在再来一个bitset<8> output,经过循环置换操作后output的结果为 "10010100"。
置换过程简单来说,就是如下图所示:从左边开始数,input中第[3,1,7,5,2,8,4,6]个位依次映射到output第[1,2,3,4,5,6,7,8]中。由于我们使用的bitset中的索引0表示低位,即从右边开始数,因此需要进行一个如代码中所示的下标转换。
2.3、置换表和常量定义
了解了2.2中的置换操作,就知道这些置换数组的重要性了。在DES算法中,我们有很多的置换表,这里和一些常量、枚举类型统一给出,若在下文遇到没见过的数组、枚举,请回这里查找:
const Byte SIZE_INPUT = 64;
const Byte SIZE_OUTPUT = 64;
const Byte SIZE_DIVIDE = 28;
const Byte NUM_SONKEY = 16;
const Byte SIZE_SONKEY = 48;
enum plainTextMode {TEXT, BINARY, HEX}; // 明文模式:文本,二进制,十六进制
enum operateMode {ENCODE, DECODE}; // 工作模式:加密,解密
enum encodeMode {ECB, CBC, CFB, OFB};// 加密模式:ECB, CBC, CFB, OFB
// 初始置换表64bit
const Byte InitPerm_Table[] = {
58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7
};
// 选择置换表1,28*2 bit,其中未出现的 8,16,24,32,40,48,56,64做奇偶校验位
const Byte PC_Table1[] = {
// Ci
57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36,
// Di
63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4
};
// 选择置换表2,6*8 bit
const Byte PC_Table2[] = {
14, 17, 11, 24, 1, 5, 3, 28,
15, 6, 21, 10, 23, 19, 12, 4,
26, 8, 16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55, 30, 40,
51, 45, 33, 48, 44, 49, 39, 56,
34, 53, 46, 42, 50, 36, 29, 32
};
// 左移位数表
const Byte LeftMove_Table[] = {
1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1
};
// 扩展表
const Byte Expansion_Table[] = {
32, 1, 2, 3, 4, 5,
4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13,
12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21,
20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29,
28, 29, 30, 31, 32, 1
};
// S盒,8*64bit
const Byte SBox_Table[][4][16] = {
{
{14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7},
{0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8},
{4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0},
{15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13},
},
{
{15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10},
{3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5},
{0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15},
{13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9},
},
{
{10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8},
{13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1},
{13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7},
{1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12},
},
{
{7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15},
{13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9},
{10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4},
{3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14},
},
{
{2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9},
{14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6},
{4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14},
{11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3},
},
{
{12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11},
{10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8},
{9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6},
{4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13},
},
{
{4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1},
{13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6},
{1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2},
{6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12},
},
{
{13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7},
{1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2},
{7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8},
{2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11},
}
};
// P盒,4*8bit
const Byte PBox_Table[] = {
16, 7, 20, 21, 29, 12, 28, 17,
1, 15, 23, 26, 5, 18, 31, 10,
2, 8, 24, 14, 32, 27, 3, 9,
19, 13, 30, 6, 22, 11, 4, 25
};
// 逆初始置换表64bit
const Byte FinalPerm_Table[] = {
40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25
};
三、算法实现
3.1、初始置换
非常的简单,有了上面2.2的置换操作DES_Permutation,我们只需要传入特定的数据即可。首先创建一个64bit的IP用作输出,其中plaintext为64bit明文输入(类型均为bitset<64>)。
bitset<SIZE_OUTPUT> IP;
DES_Permutation(plaintext, IP, InitPerm_Table, SIZE_INPUT);3.2、子密钥生成
首先需要64bit的Key映射为56bit,然后将其一分为二为Ci和Di(均为28bit)。有人可能会问64bit是怎么转成56bit的?其实很简单,回到2.3中的PC_Table1,它只有56个数,并且少了[8, 16, 24, 32, 40, 48, 56, 64]这8个下标,因此映射到K中的也只有56个bit。这正对应了本文开头时Tips所述。
接下来是对Ci和Di进行16轮的复杂操作(搞清楚一遍的原理就够了,剩下的都是for循环)。
1、首先对Ci和Di分别进行左移位操作(移几位参考LeftMove_Table表),注意这里的移位操作是循环的。也就是说,左移位溢出的位不会丢弃,而是移动到右边去。举个例子,有bitset<8> bs("10001011"),左移两位,则变为bs("00101110")。
// 旋转左移
template <typename Input>
void DES_LeftRotation(Input& bs, Byte count)
{
while( count-- )
{
Byte bit = bs[SIZE_DIVIDE - 1];
bs <<= 1;
bs[0] = bit;
}
}2、接下来,Ci和Di合并为bitset<56>的临时变量bs_merge,再使用PC_Table2表对其置换,即得到了第i个密钥Ki[i]
依次对操作1和2循环16次,即完成了子密钥的生成,以下给出生成子密钥完整代码实现:
// 生成的子密钥保存在Ki[]中
void getKeyTable(const bitset<SIZE_INPUT>& key, bitset<SIZE_SONKEY> Ki[])
{
// 交换生成56bit的K
bitset<SIZE_DIVIDE*2> K;
DES_Permutation(key, K, PC_Table1, SIZE_DIVIDE*2);
// 一分为二生成初始C0, D0
string str_K = K.to_string();
bitset<SIZE_DIVIDE> Ci(str_K.substr(0, SIZE_DIVIDE));
bitset<SIZE_DIVIDE> Di(str_K.substr(SIZE_DIVIDE));
// 生成16个子密钥
for(Byte i = 0; i < NUM_SONKEY; ++i){
// 旋转左移
DES_LeftRotation(Ci, LeftMove_Table[i]);
DES_LeftRotation(Di, LeftMove_Table[i]);
// 合并置换
bitset<2*SIZE_DIVIDE> bs_merge(Ci.to_string() + Di.to_string());
DES_Permutation(bs_merge, Ki[i], PC_Table2, SIZE_SONKEY);
}
}3.3、Feistel轮函数
同样的,对应上述生成的16个子密钥,轮函数同样需要进行16次。我们首先将经过初始置换生成的IP一分为二,变为28bit的Li和Ri。
// 生成初始L0, R0
string str_IP = IP.to_string();
bitset<SIZE_INPUT/2> Li(str_IP.substr(0, SIZE_INPUT/2)), tmpL;
bitset<SIZE_INPUT/2> Ri(str_IP.substr(SIZE_INPUT/2)) , tmpR;其中的tmpL,tmpR用于暂存原来的Li和Ri值,因为在轮函数中它们的值会变化,而最后又会用到原来的值。
接下来正式进入16轮循环。对于每一轮循环,首先用扩展表将Ri扩展至48bit,存放于Ei中。
bitset<SIZE_SONKEY> Ei; // 保存中间结果
DES_Permutation(Ri, Ei, Expansion_Table, SIZE_SONKEY);然后将扩展结果Ei与子密钥进行异或(加密过程对应第i个子密钥,解密过程对应第16-i个子密钥)。
// 与密钥Ki异或
if( opMode == ENCODE ) Ei ^= Ki[i];
else Ei ^= Ki[15 - i];再来就是对上述的Ei进行复杂的S盒映射操作,S盒是一个8*4*16的三维数组。
我们将Ei分为8组,每组6bit,共操作8次。第i次(0~7)我们使用第i个子二维数组进行操作。其中这6bit的首尾位构成行号(0~3),中间四位构成列号(0~15)。然后到S盒中取数,生成4bit的结果,累加到结果res中。因为这个过程有8轮,因此最终会生成32bit的数据。
string res = "";
for(Byte j = 0; j < SIZE_SONKEY; j += 6){
string str_col = Ei.to_string().substr(j+1, 4);
// 转化行、列
Byte row = Ei[SIZE_SONKEY-j-1]*2 + Ei[SIZE_SONKEY-j-6];
Byte col = bitset<4>(str_col).to_ulong();
// 获取S-BOX的值
Byte value = SBox_Table[j/6][row][col];
res += bitset<4>(value).to_string();
}
// 再转换回32bit
bitset<32> bs_tmp(res);最后将这32位数据最为输入,使用P盒进行置换,再将结果与上一轮的Li异或,便得到了下一轮的Ri;而下一轮的Li,则直接拷贝上一轮的Ri即可。
// P盒置换
DES_Permutation(bs_tmp, Ri, PBox_Table, SIZE_INPUT/2);
Ri ^= tmpL;
Li = tmpR;注意到这16轮算法中的最后一轮我们是不需要交换Li和Ri位置的,而我们在循环中并未做特殊处理。因此最终我们得到的预输出密文应当是Ri在左,Li在右。
bitset<64> res(Ri.to_string() + Li.to_string());
DES_Permutation(res, ciphertext, FinalPerm_Table, SIZE_OUTPUT);将预输出密文最后做一次IP逆置换,即得到了最终的密文ciphertext。至此,DES算法实现完成。
四、四种模式的实现
四种模式ECB, CBC, CFB, OFB的枚举常量encodeMode均已在前文定义,并同时定义了明文的输入类型plainTextMode以及算法的工作模式operateMode。以下四种模式我没有单独给定函数,而是集成在了2个函数中(CFB模式使用8位流密码,我单独为它写了一个函数),因此不会单独给出实现,而是给出完整代码,并加上注释。
4.1、电码本模式(ECB)
电码本模式即是对输入明文进行分组加密(通常为64bit)。由于电码本模式对任何分组都是使用同一密钥加密,因此若分组中若有相同的明文组,那么密文中也会出现几个相同的密文组。因此ECB模式特别适合于数据较少的情况,如加密一个密钥。
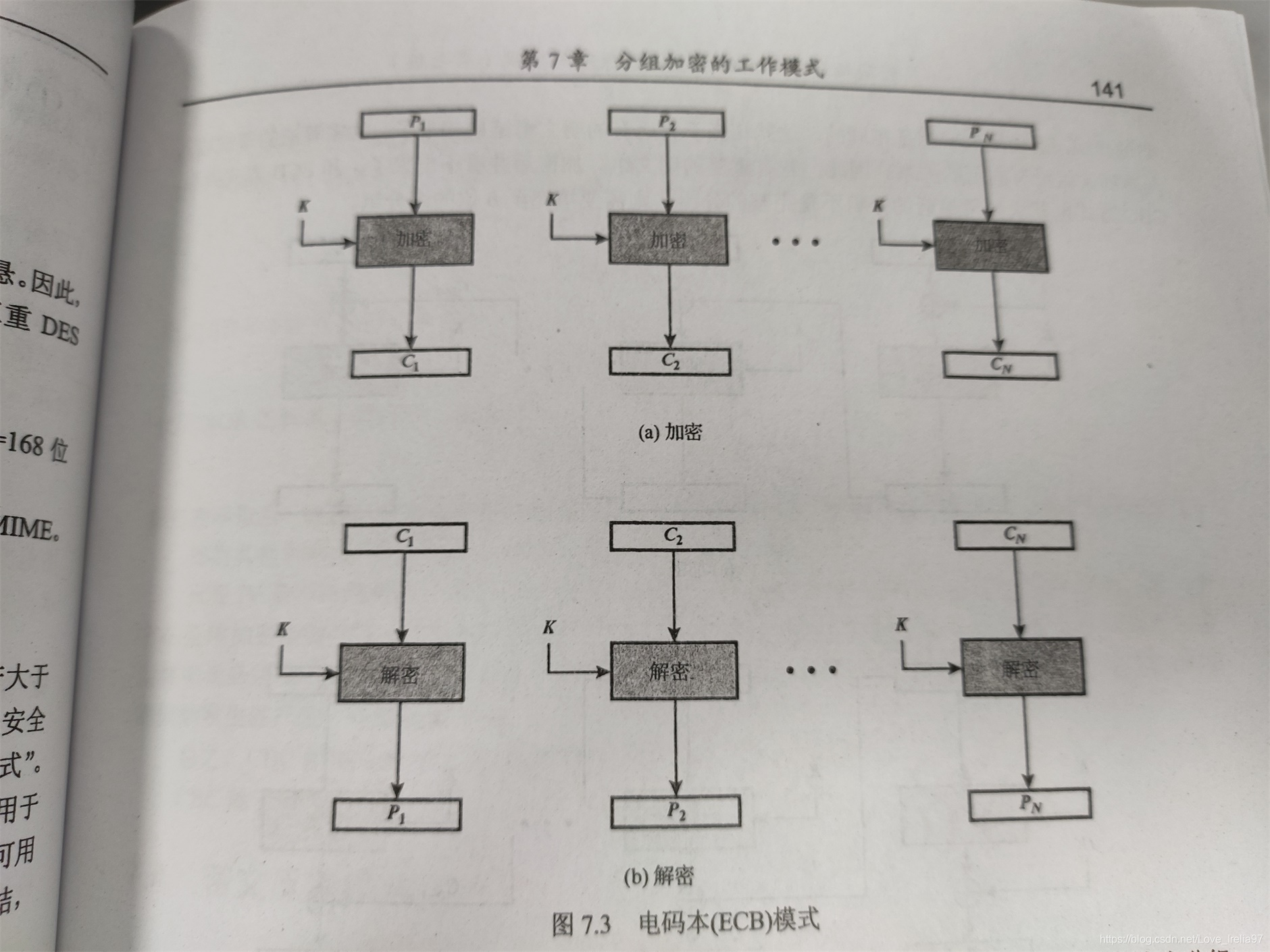
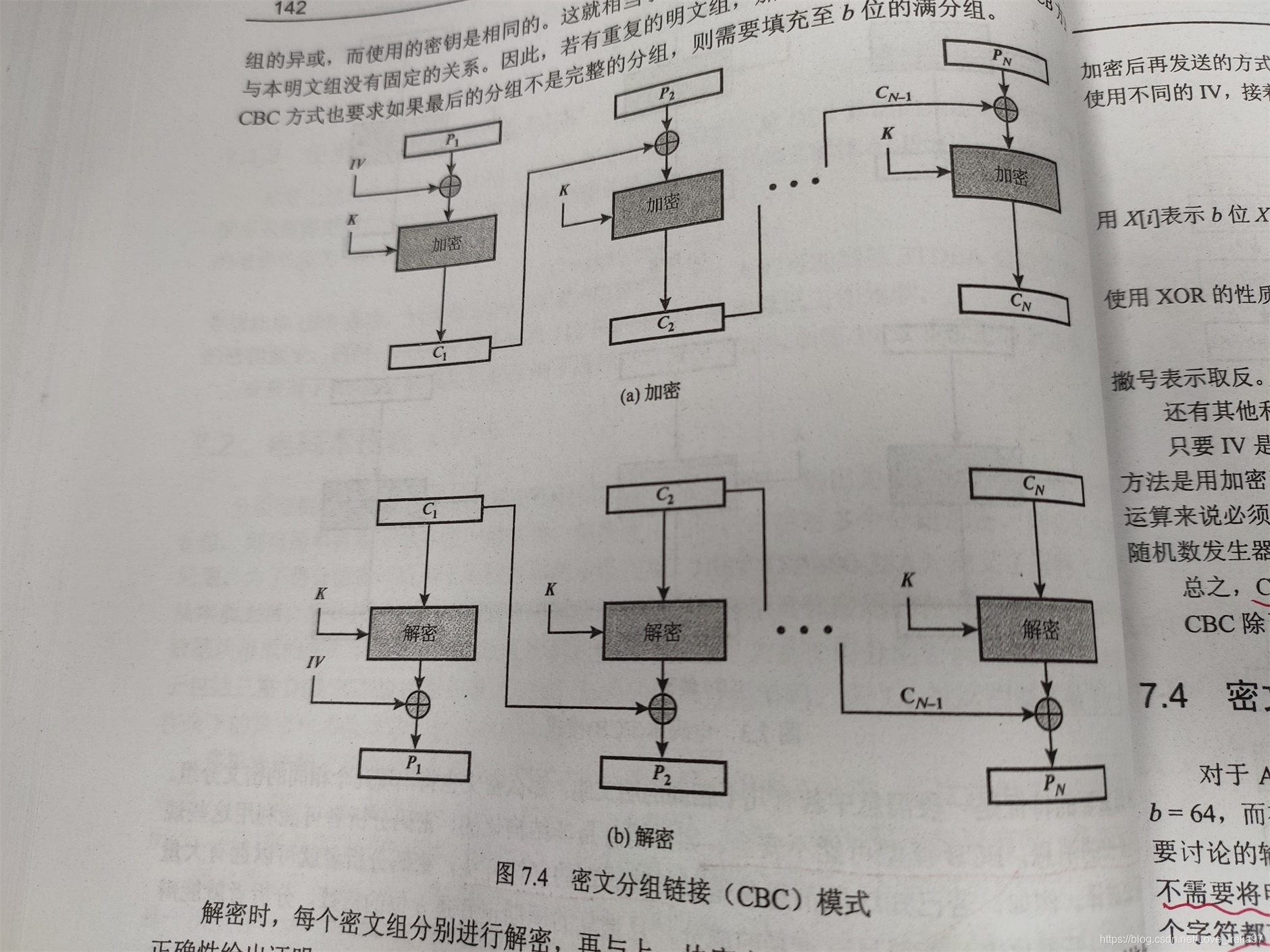
4.2、密文分组链接模式(CBC)
为了克服上述ECB的问题,我们将明文组先和上一个密文组异或,再进行相同的操作。显然,第一个分组加密时没有上一个密文组,因此我们需要设置一个64bit初始向量IV充当这个角色。
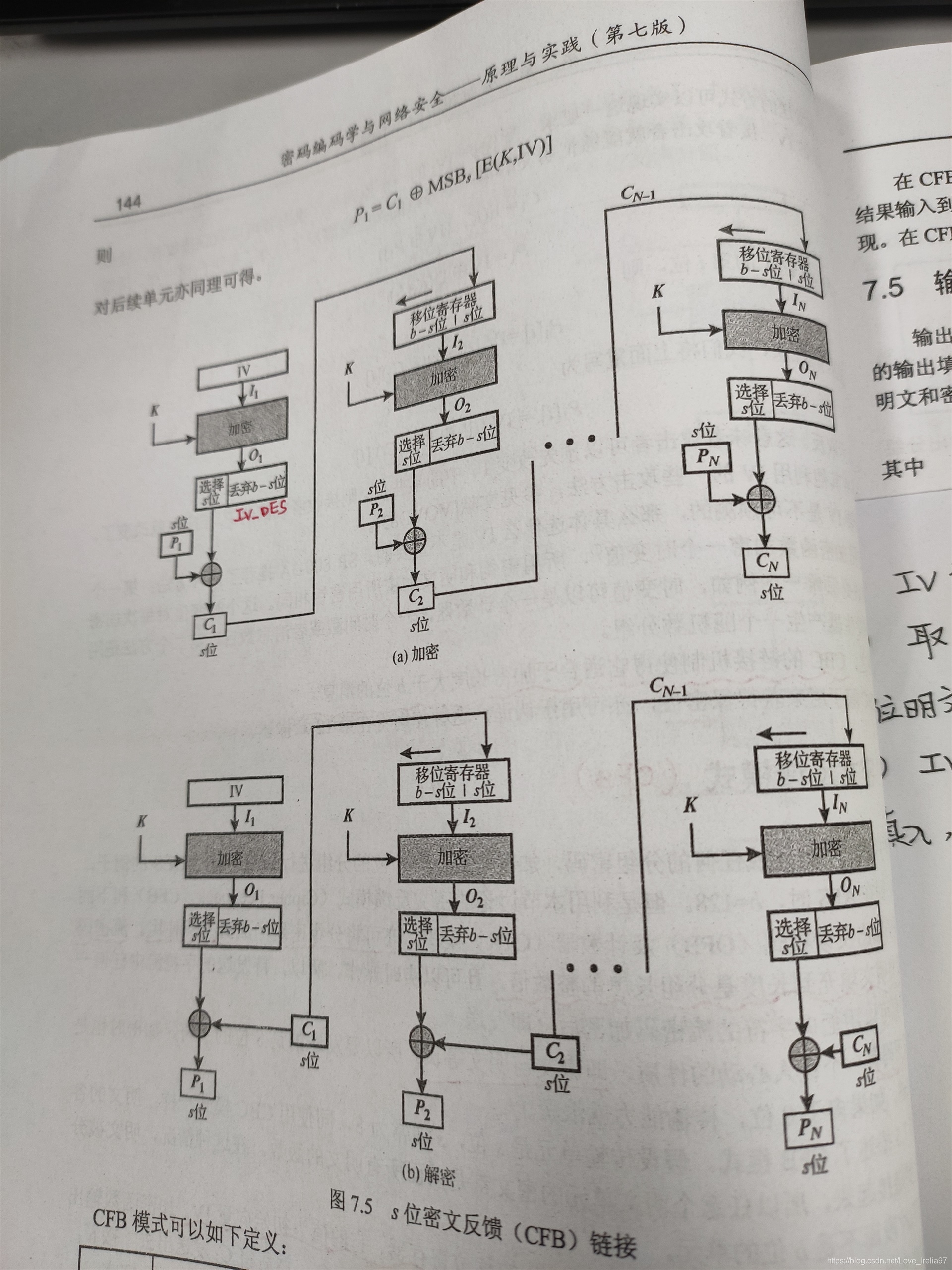
4.3、密文反馈模式(CFB)
上述两种模式都需要对明文进行64位的分组加密,若分组不够64bit的,还需要补0。在CFB模式中,我们的分组是1个字符(8个位),因此不存在这种困扰。我们同样需要一个64bit初始化向量IV充当输入,输出的IV_DES高8位与8bit明文异或得到密文;同时IV左移8位,用密文填充低8位后充当下一次的IV。特别提醒:CFB模式加/解密使用密钥Ki的顺序要一致!
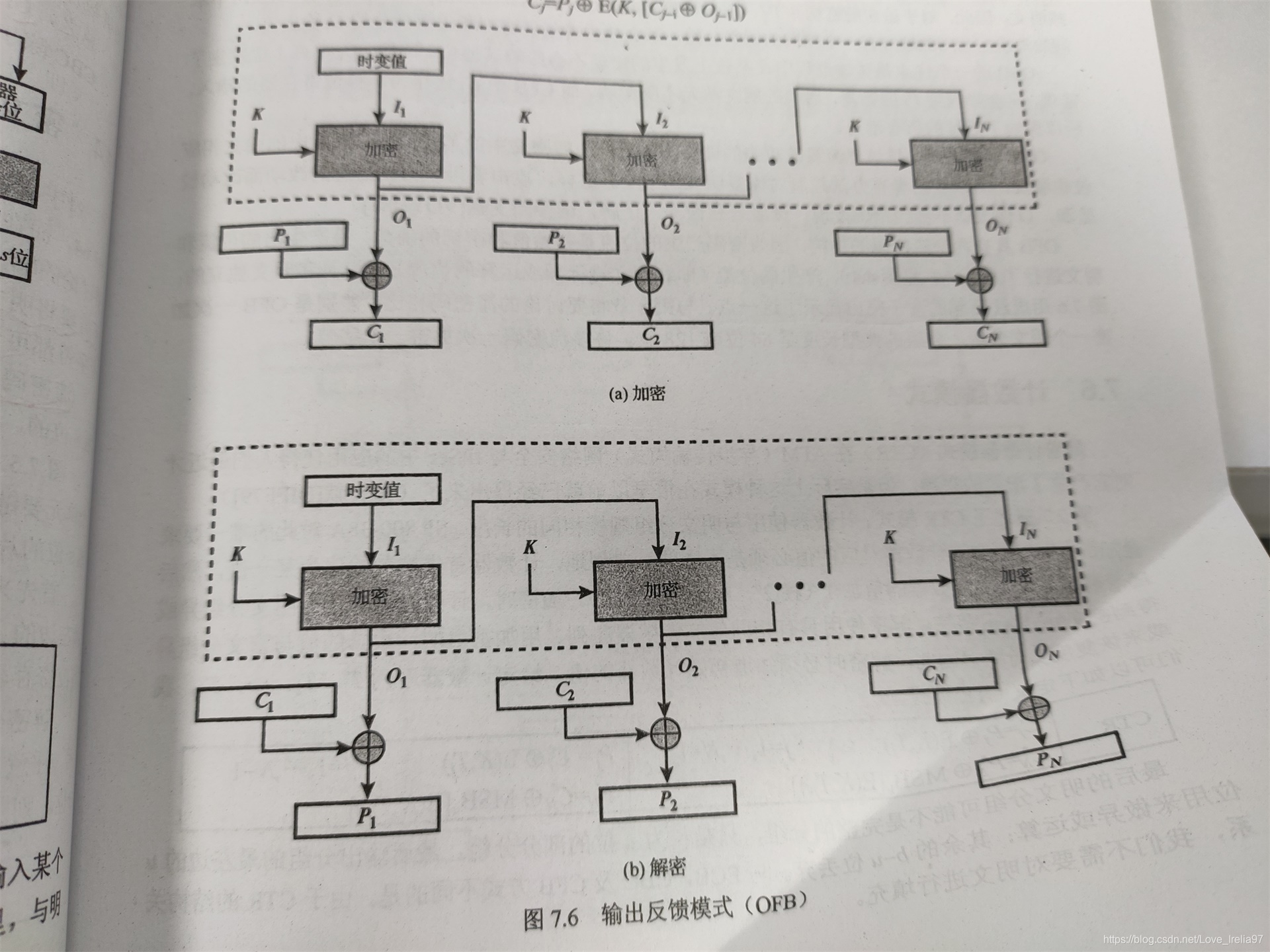
4.4、输出反馈模式(OFB)
与CFB模式类似,只是它又变回64bit分组了。因此,IV输出的IV_DES不需要取高8位,而是直接与明文分组异或。下一个IV也不需要移位填充,而是直接由IV_DES充当即可。特别提醒:OFB模式加/解密使用密钥Ki的顺序要一致!
// ECB, CBC, OFB模式实现(均以64bit分组)
string str_binaryCpText = "";
for(int i = 0; i < str_binaryPlText.size(); i += SIZE_INPUT)
{
// 每次截取64bit明文进行加密
string sub_binary = str_binaryPlText.substr(i, SIZE_INPUT);
bitset<SIZE_INPUT> plaintext(sub_binary);
bitset<SIZE_OUTPUT> ciphertext;
// ECB 电子密本模式
if( enMode == ECB ){
myDES(plaintext, Ki, ciphertext, opMode);
}
// CBC 密文分组链接模式
else if( enMode == CBC )
{
if( opMode == ENCODE )
plaintext ^= IV;
myDES(plaintext, Ki, ciphertext, opMode);
if( opMode == ENCODE )
IV = ciphertext;
else{
ciphertext ^= IV;
IV = plaintext;
}
}
// OFB 输出反馈模式
else if( enMode == OFB ){
// OFB模式加/解密时使用密钥Ki的顺序一致
myDES(IV, Ki, ciphertext, ENCODE);
IV = ciphertext;
ciphertext ^= plaintext;
}
// OFB 输出反馈模式
else if( enMode == OFB ){
// OFB模式加/解密时使用密钥Ki的顺序一致
myDES(IV, Ki, ciphertext, ENCODE);
IV = ciphertext;
ciphertext ^= plaintext;
}
// 64bit明文加密后的密文累加
str_binaryCpText += ciphertext.to_string();
}
// OFB模式需要舍去填充的位
if( enMode == OFB ){
int size = str_binaryCpText.size();
str_binaryCpText = str_binaryCpText.substr(0, size - fillSize);
} // CFB模式(8bit流分组)
string str_binaryCpText = "";
for(int i = 0; i < str_binaryPlText.size(); i += 8)
{
// 每次截取8bit明文进行加密
string sub_binary = str_binaryPlText.substr(i, 8);
bitset<8> plaintext(sub_binary);
bitset<SIZE_OUTPUT> IV_DES;
cout << "plaintext : " << plaintext << endl;
myDES(IV, Ki, IV_DES, ENCODE);
bitset<8> ciphertext(IV_DES.to_string().substr(0, 8));
ciphertext ^= plaintext;
cout << "ciphertext : " << ciphertext << endl << endl;
str_binaryCpText += ciphertext.to_string();
IV <<= 8;
if( opMode == ENCODE )
IV |= bitset<64>( ciphertext.to_string() );
else
IV |= bitset<64>( plaintext.to_string() );
}四种模式中均为对二进制流操作,而输入明文可为“文本”、“十六进制”、“二进制”,因此在这两个函数的前后还有一些文本<->进制的转换,具体函数及模式完整代码请到Github仓库中查看。