过拟合与欠拟合
我们希望机器学习得到好的模型,该模型能够从训练样本中找到一个能够适应潜在样本的普遍规律。然而,如果机器学习学的“太好”了,以至把样本的自身特点当作潜在样本的一般特性,这就使得模型的泛化能力(潜在样本的预测能力)下降,从而导致过拟合。反之,欠拟合就是学习的“太差”,连训练样本都没有学好。
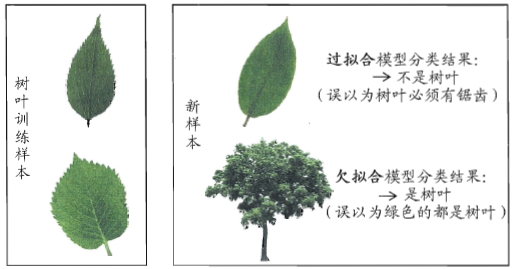
欠拟合容易处理,比如在决策树中扩展分支,在神经网络中增加训练轮数,需要重点关注的是麻烦的过拟合。
当训练数据很少时,如果使用了过多的特征,将会导致过拟合:
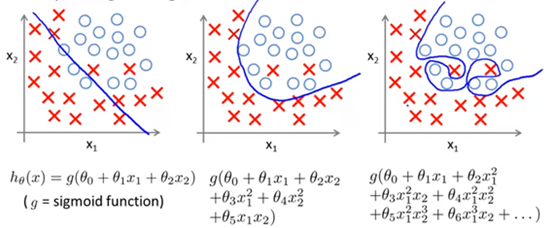
图三是一个明显的过拟合,它使用了高阶多项式增加一些特新特征,得到的复杂曲线将样本学些的“太好”了,以至失去了泛化性。
正则化
如果发生了过拟合问题,可以通过作图来观察,但是当遇到很多变量时,画图将变得困难,此时我们应该如何处理?
一种常用的办法是减少变量的选取,比如对于房价的预测,影响房价的特征可能有上百个,但其中的某些特征对结果的影响很小,例如邻居的收入,此时就可以去掉这些影响较小的变量。这类做法非常有效,但是其缺点是当你舍弃一部分特征变量时,你也舍弃了问题中的一些信息。也许所有的特征对于预测房价都是有用的,我们实际上并不想舍弃一些特征。
另一种方法就是正则化,特允许我们保留所有的特征变量。
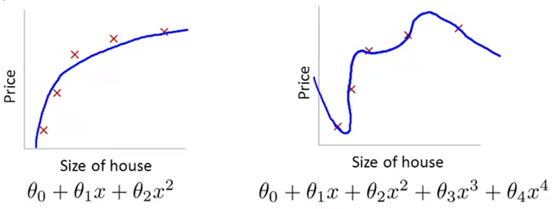
当我们有很多特征变量时,其中每一个变量都能对预测产生一点影响,在下图中,如果用一个二次函数来拟合这些数据,那么它给了我们一个对数据很好的拟合。然而,如果我们用一个更高次的多项式去拟合,最终将得到一个过拟合的复杂曲线。
如果学习策略是平方和损失函数,那么我们的目的就是找到合适的θ使得J(θ)最小化:

应对过拟合的策略就是加上惩罚项,从而使θ3和θ4足够小:

1000 只是随便写的某个较大的数字。现在,因为1000θ32和1000θ42会使J(θ)变得很大,为了最小化J(θ),需要使θ3≈0,θ4≈0,这样将得到一个近似二次函数的新函数,这会是一个更好的模型函数。最终,我们恰当地拟合了数据,所使用的正是二次函数加上一些贡献很小的特征项x3和x4 (它们对应权重接近0)。
上面的方法就是正则化的思路,如果特征值对应一个较小的权重,那么最终将会得到一个简单的假设。
在上面的例子中,由于我们知道x3和x4是重点惩罚对象(对结果影响较小),所以只惩罚它们,但是如果有很多特征,并且我们不知道如何选择关联度更好的参数,如何缩小参数的数目等等,应该如何处理呢?
因为我们并不知道是哪一个或哪几个要去缩小,因此在正则化里,需要减小代价函数中的所有特征值:
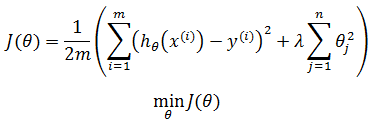
上式中n是特征的个数,λ是正则化参数。需要注意的是,惩罚项从θ1开始。按照惯例,我们没有去惩罚 θ0,因此 θ0 的值是大的,但在实践中无论是否包括θ0,差异都不大。
 称为正则化项,其目标有两个:希望假设能够很好地适应训练集,想要保持参数值较小。λ的目的就是控制二者之间的平衡,从而保持假设的形式相对简单,以避免过度的拟合。
称为正则化项,其目标有两个:希望假设能够很好地适应训练集,想要保持参数值较小。λ的目的就是控制二者之间的平衡,从而保持假设的形式相对简单,以避免过度的拟合。
对J(θ)求偏导:

如果使用梯度下降:
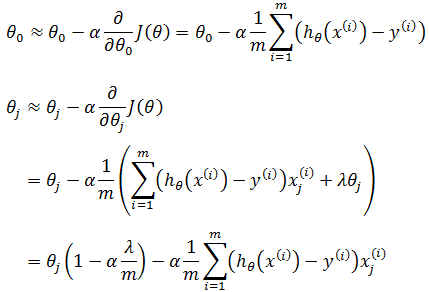
如果λ很小,则丧失了正则化的意义,相当于所有惩罚项都接近于0,这又将导致过拟合;如果λ 很大,将会非常大地惩罚参数θ1 θ2 θ3 θ4 …,最终会使所有这些参数都接近于零,导致欠拟合,如下图所示:
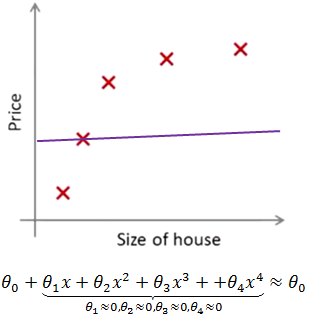
如果我们这么做,相当于去掉了θj≈0对应的特征,只留下了一个简单的假设,这个假设只能表明房屋价格等于 θ0 的值,类似于拟合了一条水平直线,对于数据来说这就是一个欠拟合,它不会去趋向大部分训练样本的任何值。
其它方法
上面的正则化方法实际上被称为L2正则化(L2 regularization),其原型是新损失函数等于原损失函数加上正则化项,其中J0(θ)表示原损失函数:
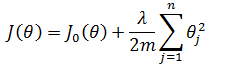
对θj求导:


L1正则假设特征是拉普拉斯分布,可以保证模型的稀疏性,也就是某些参数等于0;L1正则化导出的稀疏性质已被广泛用于特征选择,可以从可用的特征子集中选择有意义的特征。
L2正则假设特征是高斯分布,通常倾向让权值尽可能小,最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单,能适应不同的数据集,也在一定程度上避免了过拟合现象。参数足够小,数据偏移得多一点也不会对结果造成什么影响,可以说“抗扰动能力强”。
此外,还有early stopping、数据集扩增(Data augmentation)、dropout等方法能够降低过拟合。
参考:
Ng视频《Logistic Regression》
周志华《机器学习》
《机器学习导论》
作者:我是8位的
出处:http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注公众号“我是8位的”
