三分钟彻底理解堆排序

1.原理(本次以大根堆为例进行讲解，小根堆同理)：

　　利用大根堆(小根堆)堆顶记录的是最大关键字(最小关键字)的特性，使得每次可以将堆顶的最值取出依次放入数组中，最后得到一个依次增大(减小)的序列。

　　(1)大根堆堆实际上是一棵完全二叉树，其任何一个非叶节点满足：

　　　　key[i] >= k[2i+1]&&key[i]>=key[2i+2]

　　　　即任何一个非叶节点的关键字大于或等于其左右孩子的节点的关键字

2.思路：

　　(1)构建一个堆

　　(2)将其调整为大根堆(小根堆)

　　(3)取出堆顶最大值元素(最小值元素)

　　(4)剩下的数据构造最大堆(最小堆)

　　

　　构建大根堆基本的思想为(大根堆)

　　　　(1)将初始待排序的关键字序列(R1,R2.....Rn)构建成大根堆，此堆为初始的无序区

　　　　(2)将堆顶元素R[1]与最后一个元素R[n]进行交换，使得此时得到的无序区为(R1,R2,......Rn-1)和新的有序区(Rn)，并且满足R[1,2,3.....n-1]<=R(n)；

　　　　(3)由于交换后新的堆顶可能违反堆的性质，需要对当前无序区域(R1,R2,......Rn-1)调整为新的大根堆，然后再将R[1]与无序区的最后一个元素进行交换，得到新的无序区(R1,R2,.....Rn-2)和新的有序区(Rn-1，Rn)。不断重复这个过程，知道有序区的元素个数为n-1，则整个排序过程完成。

3.图解实例过程：

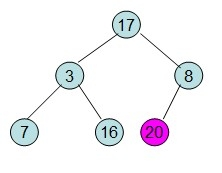
　　(1)给定一个整形数组a[]={16,7,3,20,17,8}，对其进行堆排序。

    　　首先根据该数组元素构建一个完全二叉树，得到：

　　　　

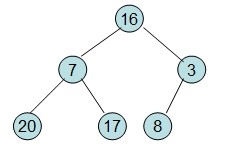
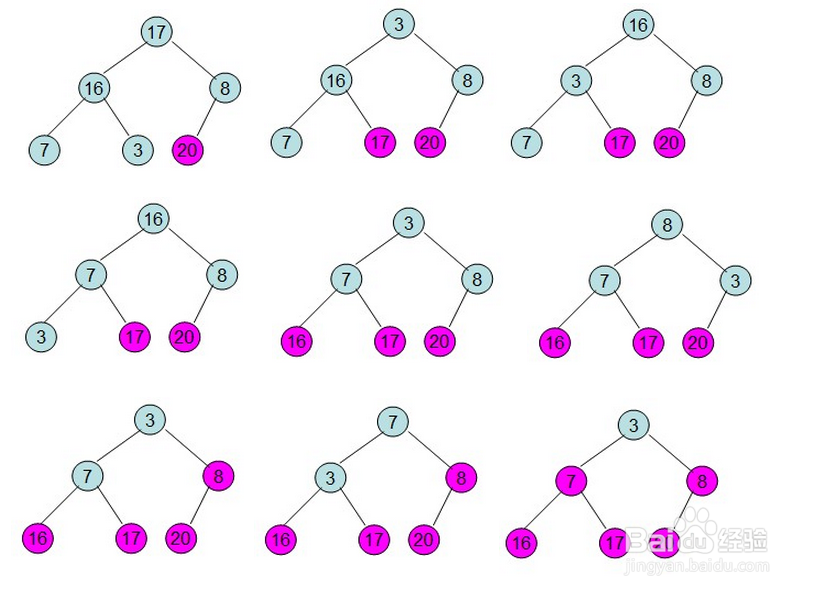
　　(2)然后需要构造初始堆，则从最后一个非叶节点开始进行调整，调整的过程如下：

　　

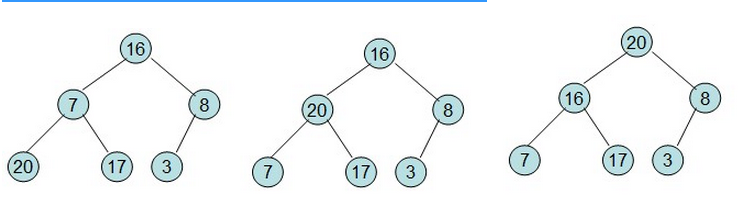
　　(3)20和16交换之后不满足堆的性质，因此需要进行重新调整，

　　

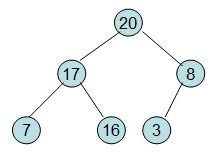
　　(4)这样就得到初始堆了。

　　即每次调整都是从父节点、左孩子节点、右孩子节点中选择最大者跟父节点进行交换(在交换之后可能造成被交换的孩子节点不再满足堆的性质，因此每次交换之后需要对交换的孩子节点进行调整)。有了初始堆之后就可以进行排序了。

　　

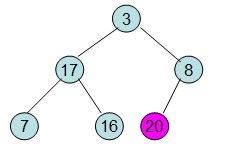
　　(4)这个时候，位于堆顶的节点3使得这个堆不再满足最大堆的性质，需要进一步进行调整。

　　

4.java代码实现：

import java.util.Arrays;

public class HeapSort {
    //test
    public static void main(String[] args) {
        int testTime = 500000;
        int maxSize = 100;
        int maxValue=100;
        boolean succeed = true;
        for(int i = 0 ; i<testTime;i++) {
            int[] arr1 = generateRandomArray(maxSize, maxValue);
            int[] arr2 = copyArray(arr1);
            heapSort(arr1);
            comparator(arr2);
            if (!isEqual(arr1, arr2)) {
                succeed = false;
                printArray(arr1);
                printArray(arr2);
                break;
            }
        }
        System.out.println(succeed?"Nice":"fucking fucked!");
        int[] arr = generateRandomArray(maxSize,maxValue);
        printArray(arr);
        heapSort(arr);
        printArray(arr);
    }
    //堆排序
    //堆是在数组中进行伸缩的，
    public static void heapSort(int[] arr){
        if(arr==null || arr.length<2){
            return;
        }
        //先创建堆，将元素插入堆中
        for(int i = 0 ;i<arr.length;i++){
            heapInsert(arr,i);
        }
        int size = arr.length;
        //将0位置的元素和树的最后一个元素的位置进行交换
        swap(arr,0,--size);
        while (size>0){ //只要树还有元素，就将树中最后一个元素的位置和树根元素进行交换
            //将交换后的堆顶元素进行调整
            heapify(arr,0,size);
            //将最后一个元素和堆顶元素记性交换
            swap(arr,0,--size);

        }

    }
    //建立大根堆的过程，时间复杂度为O(logn)
    public static void heapInsert(int[] arr,int index){
        //将元素插入堆，如果插入元素位置的元素大于父节点位置的元素，那就将这两个位置的元素位置互换
        //最终的结果是创建一个大根堆
        while (arr[index]>arr[(index-1)/2]){
            swap(arr,index,(index-1)/2);
            index = (index - 1)/2;
        }
    }
    //交换数组中两个元素的位置
    public static void swap(int[] arr,int i ,int j){
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    //当大根堆中有个位置的元素被换掉，就需要进行相应的调整
    //0-heapsize-1的范围上已经形成了堆，再往右就越界
    public static void heapify(int[] arr,int index,int size){
        //得到左孩子节点的索引
        int left = 2*index+1;
        //当左子树的下标没有超过数组长度的时候，即左孩子下标没有越界，如果left已经越界了，那就表示其父节点已经是叶子节点了
        while (left<size){
            //只有右孩子不越界，并且右孩子的值要比左孩子的值要大，才会作为largest值出现
            int largest = left+1<size&&arr[left+1]>arr[left]?left+1:left;//找出左右节点中值比较大的节点
            //左孩子和右孩子最大值和父节点index之间谁大，谁就是largest下标
            largest = arr[largest]>arr[index]?largest:index;
            //如果父节点的值比两个子节点的值都大的话，就退出
            if(largest==index){
                break;
            }
            //如果父节点的值小于两个子节点中比较大的值的节点的时候，就将父节点和子节点中值较大的进行交换
            swap(arr,largest,index);
            //这是一个值变小一直向下沉的操作
            index=largest;
            //索引交换了之后，接着向下做调整操作
            left=index*2+1;
        }
    }
    //test
    public static  int[] generateRandomArray(int maxSize,int maxValue){
        int[] arr = new int[(int) ((maxSize + 1) * Math.random())+1];
        for (int i = 0; i < arr.length; i++) {
            arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
        }
        return arr;
    }
    //test
    public static int[] copyArray(int[] arr){
        if(arr==null || arr.length==0){
            return null;
        }
        int[] res = new int[arr.length];
        for(int i = 0 ; i<arr.length;i++){
            res[i] = arr[i];
        }
        return res;
    }

    //test
    public static void comparator(int[] arr) {
        Arrays.sort(arr);
    }
    //test
    public static boolean isEqual(int[] arr1,int[] arr2){
        if((arr1!=null&&arr2==null)||(arr1==null&&arr2!=null)){
            return false;
        }
        if(arr1==null&&arr2==null){
            return true;
        }
        if(arr1.length!=arr2.length){
            return false;
        }
        for(int i = 0 ; i <arr1.length;i++){
            if(arr1[i]!=arr2[i]){
                return false;
            }
        }
        return true;

    }
    //test
    public static void printArray(int[] arr){
        if(arr==null||arr.length==0){
            return;
        }
        for(int i =0 ;i<arr.length;i++){
            System.out.print(arr[i]+" ");
        }
        System.out.println();
    }
}