快速排序
概述
快速排序算法最早由图灵奖获得者Tony Hoare设计
快速排序算法被列为20实际十大算法之一
快速排序属于交换排序类,是通过不断比较和移动交换来实现的,快速排序的实现,比其他交换排序(比如冒泡排序),增大了记录的比较和移动的距离,将关键字较大的记录从前面直接移动到后面,关键字较小的记录从后面直接移动到前面,从而减少总的比较次数和移动交换次数
快速排序算法
- 快速排序(Qucik Sort)基本思想
通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序的目的 - Go实现例子
对数组[50,10,90,30,70,40,80,60,20]进行排序
package main
import "fmt"
type quick_sort struct {
num_arr [9]int
}
func (q *quick_sort) QuickSort(low int, high int) {
var pivot int
if(low<high) {
pivot = q.Partition(low, high)//将q *quick_sort一分为二 算出枢轴值pivot
q.QuickSort(low, pivot-1)//对低子表递归排序
q.QuickSort(pivot+1, high)//对高子表递归排序
}
}
//交换子表(子数组)的记录,使枢轴记录到位,并返回其所在的位置
func (q *quick_sort) Partition(low int, high int) int {
var pivotkey int
var temp int//用于交换
pivotkey = q.num_arr[low]//用子表的第一个记录做枢轴记录
for {
if (low>=high) {
break
}
//从右边向中间扫描
//高位值大于枢轴,继续循环,执行high--
for {
if (low >= high || q.num_arr[high] <= pivotkey) {
break
}
high--
}
//高位数字小于枢轴,交换到低位
temp = q.num_arr[low]
q.num_arr[low] = q.num_arr[high]
q.num_arr[high] = temp
//从左边向中间扫描
//低位小于枢轴,继续循环,执行low--
for {
if (low >= high || q.num_arr[low] >= pivotkey) {
break
}
low++
}
//低位大于枢轴,交换到高位
temp = q.num_arr[high]
q.num_arr[high] = q.num_arr[low]
q.num_arr[low] = temp
}
return low//返回枢轴的位置
}
func main() {
var q = quick_sort{}
q.num_arr = [9]int{50,10,90,30,70,40,80,60,20}
q.QuickSort(0, len(q.num_arr)-1)
fmt.Printf("%v", q.num_arr)
}
运行后得到如下结果
go run QucikSort.go
[10 20 30 40 50 60 70 80 90]%
注释与说明
枢轴:Partition函数要做的,就是先选取数组中的一个关键字,比如选择第一个关键字50,然后想办法将它放到一个位置,使得它左边的值都比它小,右边的值都比它大,将这样的关键字称为枢轴
在经过第一调用q.Partition(0,8)之后,数组变成[20 10 40 30 50 70 80 60 90],并返回值4给pivot,表明50放在数组下标为4的位置
此时待排序数组变成两个小数组[20 10 40 30]和[70 80 60 90],对他们进行递归调用,直到顺序正确
执行过程描述
begin,low=0,high=9,将q.num_arr[0]=50赋值给pivotkey
q.num_arr[8]=20小于50,交换q.num_arr[0]与q.num_arr[8]的值,使得q.num_arr[0]=20,q.num_arr[8]=50
q.num_arr[0]=20小于50,执行low++,循环执行,直到q.num_arr[4]=90大于50,交换q.num_arr[2]与q.num_arr[8]的值,使得q.num_arr[2]=50,q.num_arr[8]=90
q.num_arr[8]=90大于50,执行high--,循环执行,直到q.num_arr[5]=40小于50,交换q.num_arr[5]与q.num_arr[4]的值,使得q.num_arr[2]=40,q.num_arr[5]=50...
...持续比较与交换值,直到low=high=4,退出循环,返回low的值4,进行递归调用,直到顺序正确
复杂度分析[TODO:分析过程待完善]
时间复杂度O(nlonn)
空间复杂度(logn)
优化
- 优化选取枢轴
- 优化必要的交换
- 优化小数组时的排序方案
- 优化递归操作
延伸
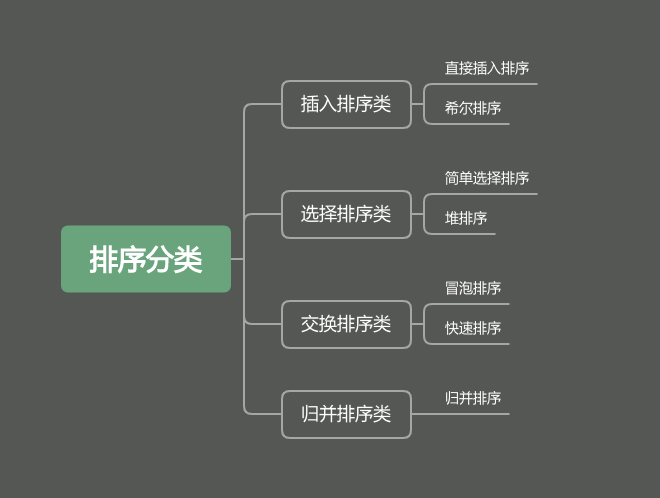
- 排序分类
根据排序过程中借助的主要操作,将内排序按下图进行分类