function spreadingability=sir(A,beta,mu)
for i=1:length(A)
for N=1:50%随机次数
InitialState=zeros(length(A),1);InitialState(i)=1;
time=5;%传播时间
I(N,:)=sire(A,InitialState,beta,mu,time);
end
spreadingability(i,1)=mean(mean(I));%节点i的传播能力
end
end
function I=sire(A,InitialState,beta,mu,time)
%******************************
% A邻接矩阵
% InitialState初始感染状态
% beta感染率
% mu恢复率
% time传播时间
%*****************************
Infected=InitialState;recover=[];
Infected_temp=zeros(size(Infected));
for t=1:1:time %一共进行时长time的演化
%%
%若i是易感节点, 则对i以一定概率进行传染
x1=find(Infected==0);
a1=rand(size(x1));
b1=beta*(A(x1,:)*Infected);%已经被感染的节点以一定概率去感染其他节点
xx1=setdiff(find(a1<b1),recover);
Infected_temp(x1(xx1))=1;%不是recover的节点以一定概率被感染
xx2=setdiff(find(a1>=b1),recover);
Infected_temp(x1(xx2))=0;%对不是recover且没被感染的其他节点保留易感状态
%%
%若i是染病节点, 则对i以一定概率进行移除(recover)
x2=find(Infected==1); %如果是已经被感染的节点
a2=rand(size(x2));
xx3=find(a2<mu);%对染病节点以一定概率进行recover
recover=[recover;xx3];%更新被recover节点;
xx4=find(a2>=mu);
Infected_temp(x2(xx4))=1;%余下未被recover的节点仍保留感染能力
Infected=Infected_temp;
I(t)=sum(Infected); %记录每个时间步的染病节点数量
end
end
susceptible-infected-recovered(SIR)传染病模型常用来计算节点影响力标准测量。在SIR模型中,节点有三个状态:易感者(susceptible),感染者(infected),恢复者(recovered)。易感者能够被感染者染病,感染者染病且有感染易感者的能力,恢复者由感染者恢复而成,不再具备感染能力同时也不会再被感染。传染病模型参数有恢复率μ,传染概率β,重复仿真次数T,仿真时间timespace。仿真过程如下:选择网络中一个节点i作为感染者节点,以传染概率β向i连接的邻居易感者节点传染病毒,被染病的节点继续以β的概率向他们的邻居易感者节点传染。同时每个染病节点在每阶段以μ的概率转变成恢复节点。当μ=0时,网络中只存在感染者和易感者,此时模型被称为Susceptible-infected(SI)模型。仿真结束后,可以得到每个节点i的传染能力Si
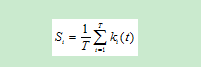
其中ki(t)表示节点第t次仿真时传染的节点个数,网络中节点传染能力S=[S1,S2,…,SN]
2018/11/20 更新:经过网友的指正,需要说明的是下面的代码是SIS传染病模型,recover节点仍具有再次被感染的能力。和SIR模型中recover节点不再被感染还是有区别的