§1 矩阵概念的一些背景
在线性方程组的讨论中,我们看到,线性方程组的一些重要性质反映在它的系数矩阵和增广矩阵的性质上,并且解线性方程组的过程也表现为变换这些矩阵的过程.除了线性方程组之外,还有大量的各种各样的问题也都提出矩阵的概念,并且这些问题的研究常常反映为有关矩阵的某些方面的研究,甚至于有些性质完全不同的、表面上完全没有联系的问题,归结成矩阵问题以后却是相同的.这使矩阵成为数学中一个极其重要的应用广泛的概念,因而也就使矩阵成为代数特别是线性代数的一个主要研究对象.
1. 在解析几何中考虑坐标变换时,如果只考虑坐标系的转轴(反时针方向转轴),那么平面直角坐标变换的公式为
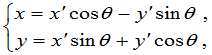 (1)
(1)
其中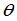 为
为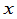 轴与
轴与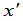 轴的夹角.显然新旧坐标之间的关系,完全通过公式中系数所排成的
轴的夹角.显然新旧坐标之间的关系,完全通过公式中系数所排成的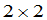 矩阵
矩阵
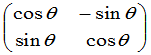 (2)
(2)
表示出来.通常,矩阵(2)称为坐标变换(1)的矩阵.在空间的情形,保持原点不动的仿射坐标系的变换有公式
 (3)
(3)
同样,矩阵
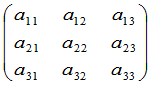 (4)
(4)
就称为坐标变换(3)的矩阵.
2. 二次曲线的一般方程为
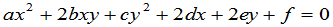 . (5)
. (5)
(5)的左端可以简单地用矩阵
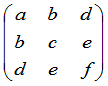 (6)
(6)
来表示.通常,(6)称为二次曲线(5)的矩阵.以后我们会看到,这种表示法不只是形式的.
3. 在讨论国民经济的数学问题中也常常用到矩阵.例如,假设在某一地区,某一种物资,比如说煤,有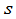 个产地
个产地 ,
,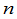 个销地
个销地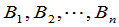 ,那么一个调动方案就可以用一个矩阵
,那么一个调动方案就可以用一个矩阵
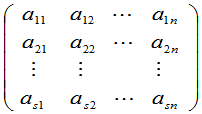
来表示,其中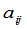 表示由产地
表示由产地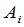 运到销地
运到销地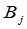 的数量.
的数量.
4. 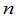 维向量也可以看成矩阵的特殊情形.
维向量也可以看成矩阵的特殊情形. 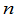 维行向量就是
维行向量就是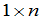 矩阵,
矩阵, 维列向量就是
维列向量就是 矩阵.
矩阵.
以后用大写的拉丁字母 ,或者
,或者
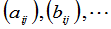
来表示矩阵.
有时候,为了指明所讨论的矩阵的级数,可以把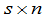 矩阵写成
矩阵写成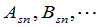 ,或者
,或者
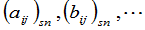
(注意矩阵符号与行列式的符号的区别).
设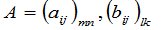 ,如果
,如果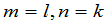 ,且
,且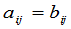 ,对
,对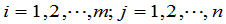 都成立,我们就说
都成立,我们就说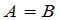 .即只有完全一样的矩阵才叫做相等.
.即只有完全一样的矩阵才叫做相等.
§2 矩阵的运算
现在来定义矩阵的运算,它们可以认为是矩阵之间一些最基本的关系.下面要定义矩阵的加法、乘法、矩阵与数的乘法以及矩阵的转置.
为了确定起见,我们取定一个数域,以下所讨论的矩阵全是由数域中的数组成的.
1. 加法
定义1 设
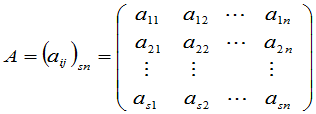 ,
,
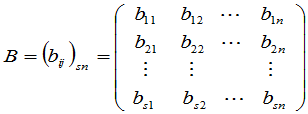
是两个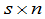 矩阵,则矩阵
矩阵,则矩阵

称为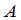 和
和 的和,记为
的和,记为
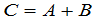 .
.
矩阵的加法就是矩阵对应的元素相加.当然,相加的矩阵必须要有相同的行数和列数.由于矩阵的加法归结为它们的元素的加法,也就是数的加法,所以不难验证,它有
结合律: ;
;
交换律: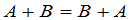 .
.
元素全为零的矩阵称为零矩阵,记为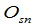 ,在不致引起含混的时候,可简单地记为
,在不致引起含混的时候,可简单地记为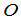 .显然,对所有的
.显然,对所有的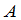 ,
,
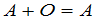 .
.
矩阵
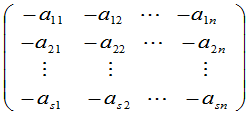
称为矩阵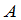 的负矩阵,记为
的负矩阵,记为 .显然有
.显然有

矩阵的减法定义为
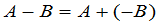
例如 在§1我们看到,某一种物资如果有 个产地,
个产地,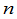 个销地,那么一个调动方案就可表示为一个
个销地,那么一个调动方案就可表示为一个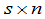 矩阵.矩阵中的元素
矩阵.矩阵中的元素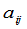 表示由产地
表示由产地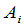 要运到销地
要运到销地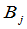 的这个物资的数量,比如说吨数.如果从这些产地还有另一个物资要运到这些销地,那么,这种物资的调动方案也可以表示为一个矩阵.于是从产地到销地的总的运输量也可以表示为一个
的这个物资的数量,比如说吨数.如果从这些产地还有另一个物资要运到这些销地,那么,这种物资的调动方案也可以表示为一个矩阵.于是从产地到销地的总的运输量也可以表示为一个 矩阵.显然,这个矩阵就等于上面两个矩阵的和.
矩阵.显然,这个矩阵就等于上面两个矩阵的和.
根据矩阵加法的定义应用关于向量组的秩的性质,很容易看出:
秩(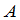 +
+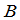 )≤ 秩(
)≤ 秩(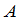 )+秩(
)+秩(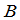 )
)
2. 乘法
在给出乘法定义之前,先看一个引出矩阵问题.
设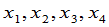 和
和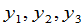 是两组变量,它们之间的关系为
是两组变量,它们之间的关系为
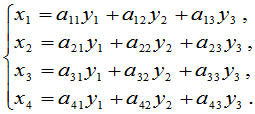 (1)
(1)
又如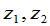 是第三组变量,它们与
是第三组变量,它们与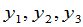 的关系为
的关系为
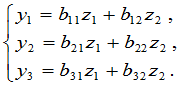 (2)
(2)
由(1)与(2)不难看出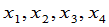 与
与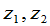 的关系:
的关系:
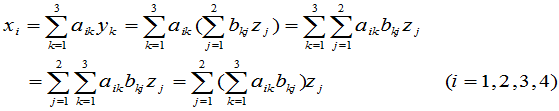 . (3)
. (3)
如果我们用
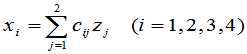 (4)
(4)
来表示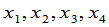 与
与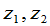 的关系,比较(3),(4),就有
的关系,比较(3),(4),就有
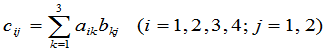 . (5)
. (5)
用矩阵的表示法,我们可以说,如果矩阵

分别表示变量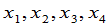 与
与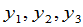 以及
以及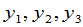 与
与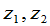 之间的关系,那么表示
之间的关系,那么表示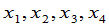 与
与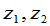 之间的关系的矩阵
之间的关系的矩阵

就由公式(5)决定.矩阵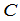 称为矩阵
称为矩阵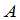 与
与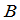 的乘积,记为
的乘积,记为
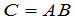
一般地,我们有:
定义2 设
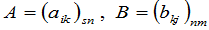 ,
,
那么矩阵
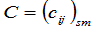 ,
,
其中
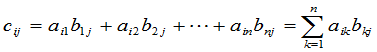 , (6)
, (6)
称为矩阵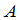 与
与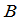 的乘积,记为
的乘积,记为
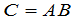 .
.
由矩阵乘法的定义可以看出,矩阵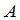 与
与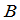 的乘积
的乘积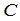 的第
的第 行第
行第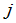 列的元素等于第一个矩阵
列的元素等于第一个矩阵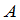 的第
的第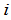 行与第二个矩阵
行与第二个矩阵 的第
的第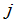 列的对应元素的乘积的和.当然,在乘积的定义中,我们要求第二个矩阵的行数与第一个矩阵的列数相等.
列的对应元素的乘积的和.当然,在乘积的定义中,我们要求第二个矩阵的行数与第一个矩阵的列数相等.
例1 设
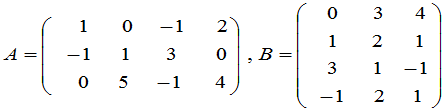 ,
,
那么
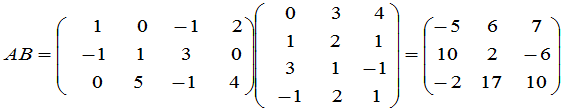
例2 如果
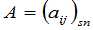
是一线性方程组的系数矩阵,而

分别是未知量和常数项所成的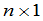 和
和 矩阵,那么线性方程组就可以写成矩阵的等式
矩阵,那么线性方程组就可以写成矩阵的等式
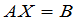 .
.
例3 在空间中作一坐标系的转轴.设由坐标系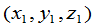 到
到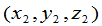 的坐标变换的矩阵为
的坐标变换的矩阵为

如果令
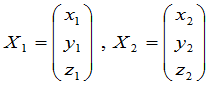 ,
,
那么坐标变换的公式可以写成
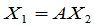 .
.
如果再作一次坐标系的转轴,设由第二个坐标系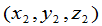 到第三个坐标系
到第三个坐标系 的坐标变换公式为
的坐标变换公式为
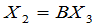 ,
,
其中
 .
.
那么不难看出,由第一个坐标系到第三个坐标系的坐标变换的矩阵即为
 .
.
矩阵的乘法适合结合律.设

则
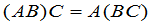 .
.
但是矩阵的乘法不适合交换律,即一般说来
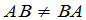 .
.
例如,设
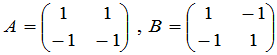
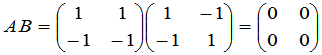 ,
,
而
 .
.
由这个例子我们还可看出,两个不为零的矩阵的乘积可以是零,这是矩阵乘法的一个特点.由此还可得出矩阵消去律不成立.即当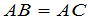 时,不一定有
时,不一定有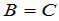 .
.
定义3 主对角线上的元素全是1,其余元素全是0的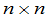 矩阵
矩阵
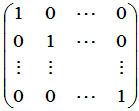
称为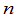 级单位矩阵,记为
级单位矩阵,记为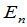 ,或者在不致引起含混的时候简单写为
,或者在不致引起含混的时候简单写为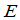 .显然有
.显然有
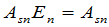 ,
,
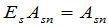 .
.
矩阵的乘法和加法还适合分配律,即
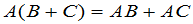 , (9)
, (9)
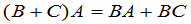 . (10)
. (10)
应该指出,由于矩阵的适合交换律,所以(9)与(10)是两条不同的规律.
我们还可以定义矩阵的方幂.设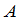 是一
是一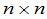 矩阵,定义
矩阵,定义
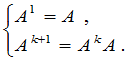
换句话说,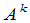 就是
就是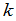 个
个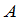 连乘.当然只能对行数与列数相等的矩阵来定义.由乘法的结合律,不难证明
连乘.当然只能对行数与列数相等的矩阵来定义.由乘法的结合律,不难证明
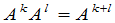 ,
,
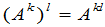 .
.
这里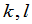 是任意正整数.因为矩阵乘法不适合交换律,所以
是任意正整数.因为矩阵乘法不适合交换律,所以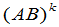 与
与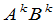 一般不相等.
一般不相等.
3. 数量乘法
. 定义4 矩阵
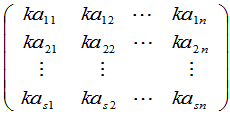
称为矩阵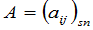 与数
与数 的数量乘积,记为
的数量乘积,记为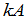 .换句话说,用数
.换句话说,用数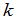 乘矩阵就是把矩阵的每个元素都乘上
乘矩阵就是把矩阵的每个元素都乘上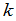 .
.
数量乘积适合以下的规律:
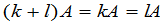 , (11)
, (11)
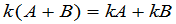 , (12)
, (12)
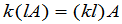 , (13)
, (13)
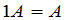 , (14)
, (14)
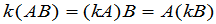 . (15)
. (15)
矩阵
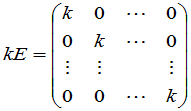
通常称为数量矩阵.作为(15)的特殊情形,如果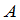 是一
是一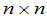 矩阵,那么有
矩阵,那么有
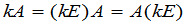 .
.
这个式子说明,数量矩阵与所有的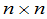 矩阵作乘法是可交换的.可以证明:如果一个
矩阵作乘法是可交换的.可以证明:如果一个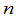 级矩阵与所有
级矩阵与所有 级矩阵作乘法是可交换的,那么这个矩阵一定是数量矩阵.再有
级矩阵作乘法是可交换的,那么这个矩阵一定是数量矩阵.再有
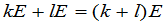 ,
,
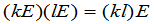 ,
,
这就是说,数量矩阵的加法与乘法完全归结为数的加法与乘法.
4. 转置
把一矩阵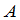 的行列互换,所得到的矩阵称为
的行列互换,所得到的矩阵称为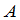 的转置,记为
的转置,记为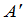 .可确切地定义如下:
.可确切地定义如下:
定义5 设
 ,
,
所谓的转置就是指矩阵
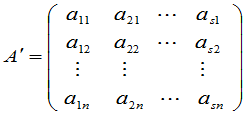 .
.
显然,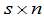 矩阵的转置是
矩阵的转置是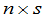 矩阵.
矩阵.
矩阵的转置适合以下的规律:
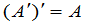 , (16)
, (16)
 , (17)
, (17)
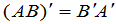 , (18)
, (18)
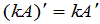 . (19)
. (19)
(16)表示两次转置就还原,这是显然的.
例4 设
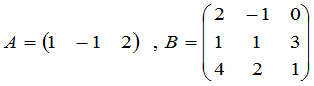
求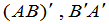 .
.
§3 矩阵乘积的行列式与秩
定理1 设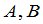 是数域
是数域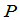 上的两个
上的两个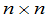 矩阵,那么
矩阵,那么
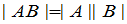 , (1)
, (1)
即矩阵乘积的行列式等于它的因子的行列式的乘积.
用数学归纳法,定理1可以推广到多个因子的情形,即有
推论1 设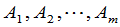 是数域
是数域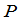 上的
上的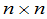 矩阵,于是
矩阵,于是
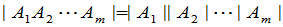
定义6 数域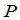 上的
上的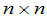 矩阵
矩阵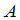 称为非退化的,如果
称为非退化的,如果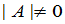 ,否则称为退化的.
,否则称为退化的.
显然一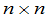 矩阵是非退化的充要条件是它的秩等于
矩阵是非退化的充要条件是它的秩等于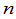 .
.
推论2 设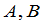 是数域
是数域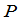 上
上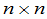 矩阵,矩阵
矩阵,矩阵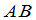 为退化的充要条件是
为退化的充要条件是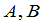 中至少有一个是退化的.
中至少有一个是退化的.
定理2 设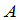 是数域
是数域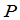 上
上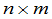 矩阵,
矩阵,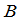 是数域
是数域 上
上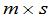 矩阵,于是
矩阵,于是
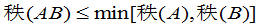 , (2)
, (2)
即乘积的秩不超过各因子的秩.
用数学归纳法,定理2可以推广到多个因子的情形,即有
推论3 如果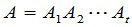 ,那么
,那么
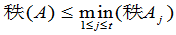 .
.
§4 矩阵的逆
一、可逆矩阵的概念
在§2我们看到,矩阵与复数相仿,有加、减、乘三种运算.矩阵的乘法是否也和复数一样有逆运算呢?这就是本节所要讨论的问题.
这一节矩阵,如不特别声明,都是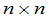 矩阵.
矩阵.
对于任意的级方阵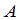 都有
都有
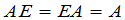
这里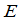 是
是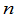 级单位矩阵.因之,从乘法的角度来看,
级单位矩阵.因之,从乘法的角度来看,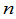 级单位矩阵在级方阵中的地位类似于1在复数中的地位.一个复数
级单位矩阵在级方阵中的地位类似于1在复数中的地位.一个复数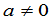 的倒数可以用等式
的倒数可以用等式
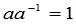
来刻划,相仿地,我们引入
定义7
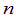 级方阵
级方阵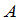 称为可逆的,如果有
称为可逆的,如果有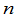 级方阵
级方阵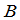 ,使得
,使得
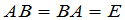 , (1)
, (1)
这里 是
是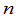 级单位矩阵.
级单位矩阵.
首先我们指出,由于矩阵的乘法规则,只有方阵才能满足(1).其次,对于任意的矩阵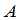 ,适合等式(1)的矩阵
,适合等式(1)的矩阵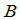 是唯一的(如果有的话).
是唯一的(如果有的话).
定义8 如果矩阵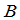 适合(1),那么
适合(1),那么 就称为
就称为 的逆矩阵,记为
的逆矩阵,记为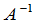 .
.
二、可逆矩阵的逆矩阵的求法
下面要解决的问题是:在什么条件下矩阵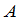 是可逆的?如果
是可逆的?如果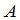 可逆,怎样求
可逆,怎样求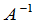 ?
?
定义9 设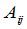 是矩阵
是矩阵
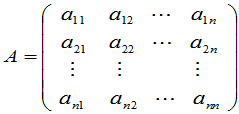
中元素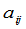 的代数余子式,矩阵
的代数余子式,矩阵
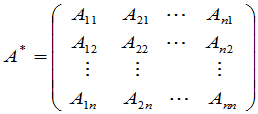
称为矩阵 的伴随矩阵.
的伴随矩阵.
由行列式按一行(列)展开的公式立即得出:
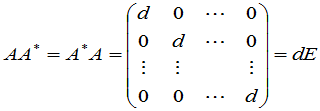 , (2)
, (2)
其中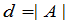 .
.
如果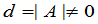 ,那么由(2)得
,那么由(2)得
 . (3)
. (3)
定理3 矩阵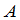 可逆的充要条件是
可逆的充要条件是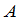 非退化的,而
非退化的,而
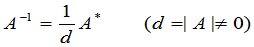
根据定理3容易看出,对于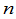 级方阵
级方阵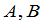 ,如果
,如果
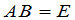
那么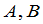 就都是可逆的并且它们互为逆矩阵.
就都是可逆的并且它们互为逆矩阵.
定理3不但给出了一矩阵可逆的条件,同时也给出了求逆矩阵的公式(4).按这个公式来求逆矩阵,计算量一般是非常大的.在以后我们将给出另一种求法.
由(5)可以看出,如果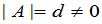 ,那么
,那么

推论 如果矩阵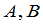 可逆,那么
可逆,那么 与
与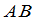 也可逆,且
也可逆,且
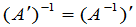
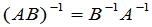 .
.
利用矩阵的逆,可以给出克拉默法则的另一种推导法.线性方程组
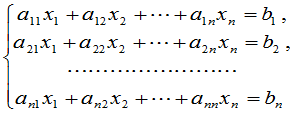
可以写成
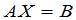 . (6)
. (6)
如果 ,那么
,那么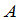 可逆.用
可逆.用

代入(6),得恒等式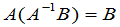 ,这就是说
,这就是说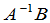 是一个解.
是一个解.
如果
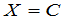
是(6)的一个解,那么由

得
 ,
,
即
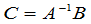 .
.
这就是说,解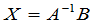 是唯一的.用
是唯一的.用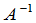 的公式(4)代入,乘出来就是克拉默法则中给出的公式.
的公式(4)代入,乘出来就是克拉默法则中给出的公式.
定理4
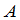 是一个
是一个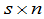 矩阵,如果
矩阵,如果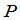 是
是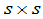 可逆矩阵,
可逆矩阵,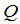 是
是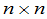 可逆矩阵,那么
可逆矩阵,那么
秩( )=秩(
)=秩(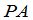 )=秩(
)=秩(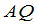 ).
).
