第二节 初等方阵
定义3 由单位矩阵经过一次的初等变换得到的方阵称为初等方阵。
三个对行的初等变换对应着三个初等方阵。
(1)互换E的i,j两行所得矩阵,记为


(2)用任意k≠0去乘E的第i行所得矩阵,记为


(3)把E的第i行乘以k加于第j行所得矩阵,记为


同样,三个对列的初等变换也对应着三个初等矩阵,分别记为





用初等方阵左乘(或右乘)任意矩阵,可达到对其进行同类型初等行(或列)变换一样的效果,现以任意3×4阶矩阵为例来说明这一点。
设

三个3阶行初等矩阵设为:
 ,
,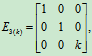


实现了A的第1,2行对换。

实现了A的第3行乘k


实现了A的第3行乘k加于第一行。
同样地,再设三个4阶列初等方阵为
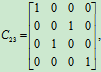 ,
,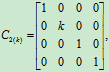

则

实现了A的第2,3两列的对换。

实现了A的第2列乘k


实现了A的第1列乘k加于第3列。
由上面的例子可得下面重要定理。
定理1 设A为任意m×n阶矩阵,对A的行施以某种初等行变换的结果相当于用同种的m阶初等方阵去左乘A;对A的列施以某种初等列变换的结果相当于用同种的n阶初等方阵去右乘A。即为:





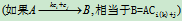
注意:左乘Am×n的是m阶初等方阵,实现的是初等行变换;右乘Am×n的是n阶初等方阵,实现的是初等列变换。
由定理1得下面的推论
推论 如果A经过若干次初等行变换得到B,那么必有若干个初等方阵E1,E2,…,Ek,使得B= E1E2…EkA;
如果A经过若干次初等列变换得到B,那么必有若干个初等方阵C1,C2,…,Cl, 使得B=AC1C2…Cl,
如果A~B,那么必有有限个初等方阵E1,E2,…,Ek, C1,C2,…,Cl,使得B= E1E2…Ek AC1C2…Cl。
定理2 任何一个初等矩阵均有逆,且其逆为同一种类型的初等矩阵。
证明:

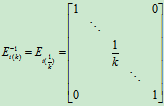
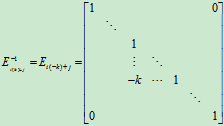
同理可证:
定理3 若A为可逆矩阵,则它恒为若干个初等方阵之积。
证明:因为A为可逆矩阵,所以A~En,由推论1可得:必有有限个初等方阵E1,E2,…,Ek, C1,C2,…,Cl,使得
En = E1E2…Ek AC1C2…Cl
再由定理2得:每个初等矩阵均可逆,于是
 ,
,
又 也是初等方阵,所以得A恒等于若干个初等方阵之积。
也是初等方阵,所以得A恒等于若干个初等方阵之积。
根据定理1和定理3可得出一种求逆矩阵的方法。
因为A可逆,则A-1也可逆,故有初等方阵L1,L2,…,Lr,使得
A-1 =L1L2…Lr。
观察下面两个等式:
A-1 A=L1L2…LrA=E
A-1 E=L1L2…LrE= A-1
第一式表明:经过若干次初等行变换可将A化为单位矩阵E;第二式表明:经过若干次同样的初等行变换可将E化为A-1。
因此可先将n阶可逆方阵A与n阶单位阵E放在一起,得到一个n×2n阶矩阵, ,再对其施以初等行变换,把子块A化为E,同时子块E化为A-1。
,再对其施以初等行变换,把子块A化为E,同时子块E化为A-1。

这是常用的矩阵求逆的方法之一。
例3 已知矩阵 ,求矩阵A的逆。
,求矩阵A的逆。
解:对 矩阵进行初等行变换
矩阵进行初等行变换



同样也可以利用初等列变换来求逆矩阵,这时对2n×n阶矩阵 施以初等列变换,当把上半子块A化为E时,下半子块E就化为A-1。
施以初等列变换,当把上半子块A化为E时,下半子块E就化为A-1。
例4 求矩阵
解:对矩阵 进行初等列变换
进行初等列变换
 =
=


