导数公式


基本积分表:
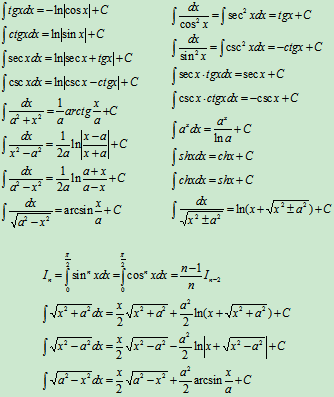

三角函数的有理式积分:

一些初等函数:


两个重要极限:

三角函数公式:
·诱导公式:
|
函数 角A |
sin |
cos |
tg |
ctg |
|
-α |
-sinα |
cosα |
-tgα |
-ctgα |
|
90°-α |
cosα |
sinα |
ctgα |
tgα |
|
90°+α |
cosα |
-sinα |
-ctgα |
-tgα |
|
180°-α |
sinα |
-cosα |
-tgα |
-ctgα |
|
180°+α |
-sinα |
-cosα |
tgα |
ctgα |
|
270°-α |
-cosα |
-sinα |
ctgα |
tgα |
|
270°+α |
-cosα |
sinα |
-ctgα |
-tgα |
|
360°-α |
-sinα |
cosα |
-tgα |
-ctgα |
|
360°+α |
sinα |
cosα |
tgα |
ctgα |
和差角公式:

和差化积公式:

·倍角公式:


·半角公式:

·正弦定理:
·余弦定理:
·反三角函数性质:
高阶导数公式——莱布尼兹(Leibniz)公式:

中值定理与导数应用:

曲率:

定积分的近似计算:

定积分应用相关公式:

空间解析几何和向量代数:


多元函数微分法及应用


微分法在几何上的应用:

方向导数与梯度:

多元函数的极值及其求法:

重积分及其应用:

柱面坐标和球面坐标:

曲线积分:


曲面积分:

高斯公式:

斯托克斯公式——曲线积分与曲面积分的关系:

常数项级数:

级数审敛法:


绝对收敛与条件收敛:

幂级数:

函数展开成幂级数:

一些函数展开成幂级数:

欧拉公式:

三角级数:

傅立叶级数:

周期为 的周期函数的傅立叶级数:
的周期函数的傅立叶级数:

微分方程的相关概念:

一阶线性微分方程:

全微分方程:

二阶微分方程:

二阶常系数齐次线性微分方程及其解法:


|
|
(*)式的通解 |
|
两个不相等实根 |
|
|
两个相等实根 |
|
|
一对共轭复根
|
|
二阶常系数非齐次线性微分方程









