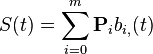在数学的子学科数值分析里,B-样条是样条曲线一种特殊的表示形式。它是B-样条基曲线的线性组合。B-样条是贝兹曲线的一种一般化,可以进一步推广为非均匀有理B样条(NURBS),使得我们能给更多一般的几何体建造精确的模型。
De Boor算法是一个数值上稳定的计算B样条的方法。
术语 B样条是Isaac Jacob Schoenberg创造的,是基(basis)样条的缩略
定义
给定m+1 个节点ti ,分布在[0,1]区间,满足
一个n次B样条是一个参数曲线:
它由n次B样条基(basis B-spline)组成
![\mathbf{S}(t)= \sum_{i=0}^{m} \mathbf{P}_{i} b_{i,n}(t) \mbox{ , } t \in [0,1]](http://upload.wikimedia.org/math/7/f/e/7febb8465828124f24debde5275e81b6.png) .
.
Pi称为控制点或de Boor点. 多边形可以通过把de Boor点用线连起来构造出来,从P0开始,到Pn结束。这样的多边形称为de Boor多边形.
m+1个n次B样条基可以用Cox-de Boor递归公式 定义
当节点等距,称B样条为均匀(uniform)否则为非均匀(non-uniform)。
均匀B样条
当B样条是均匀的时候,对于给定的n,每个B样条基是其他基的平移拷贝而已。一个可以作为替代的非递归定义是
满足
满足
其中
- (ti − t) +
是截断幂函数(truncated power function)
注解
当节点数和多项式次数相等时,B样条退化为Bezier曲线。即函数的形状由节点的位置决定。缩放或者平移节点向量不会改变基函数。
样条包含在它的控制点的凸包中
n次B样条的一个基
- bi,n(t)
仅当在区间[ti, ti+n+1]上非0。就是
换句话说,如果我们操作一个控制点,我们只改变曲线在局部的行为,而不像Bezier曲线那样是全局行为。
例子
常数B样条
常数B样条是最简单的样条。只定义在一个节点距离上,而且不是节点的函数。它只是不同节点段(knot span)的标志函数(indicator function)。
线性B样条
线性B样条定义在两个相邻的节点段上,在节点连续但不可微。
三次B样条
一个片断上的B样条的表达式可以写作:
其中Si是第i个B样条片断而P是一个控制点集,i和k是局部控制点索引。控制点的集合会是 的集合,其中wi是比重,当它增加时曲线会被拉向控制点Pi,在减小时则把曲线远离该点。
的集合,其中wi是比重,当它增加时曲线会被拉向控制点Pi,在减小时则把曲线远离该点。
片段的整个集合m-2条曲线(S3,S4,...,Sm)由m+1个控制点(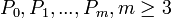 )定义,作为t上的一个B样条可以定义为
)定义,作为t上的一个B样条可以定义为
其中i是控制点数,t是取节点值的全局参数。这个表达式把B样条表示为B样条基函数的线性组合,这也是这个名称的原因。
有两类B样条-均匀和非均匀。非均匀B样条相邻控制点间的距离不一定要相等。一个一般的形式是区间随着插入控制点逐步变小到0。

![\mathbf{S}:[0,1] \to \mathbb{R}^2](http://upload.wikimedia.org/math/5/9/6/596c680504f3192b3f688f8ccbd168a8.png)
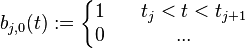


![b_n(t) := (m+1) \sum_{i=0}^{m+1} \omega_i(t_i - t)_+^{m} \qquad \mbox{ , } t \in [0,1]](http://upload.wikimedia.org/math/2/0/1/201775b9e4b0bca9e4f936695169f16d.png)
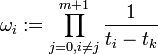


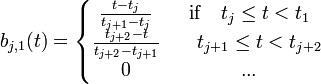
![S_{i} (t) = \sum_{k=0}^3 \mathbf{P}_{i-3+k} b_{i-3+k,3} (t) \qquad \mbox{ , } t \in [0,1]](http://upload.wikimedia.org/math/5/f/f/5fff9b2843b9cd9904c3a6253509dd54.png)