多次回归分析
在线性回归分析的时候,我用了一条直线去拟合年龄和工资的数据,结果不是太贴合的。我们尝试先用多次方程组来拟合数据。
我们先把数据读出出来。
import tensorflow as tf
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
unrate = pd.read_csv('SD.csv')
unrate = unrate.sort_values('Year')
print(unrate)
Year Salary
0 1.0 39451
30 1.1 40343
1 1.2 46313
31 1.3 47605
2 1.4 37839
.. ... ...
85 12.0 106247
86 12.5 117634
87 12.6 113300
88 13.3 123056
89 13.5 122537
[90 rows x 2 columns]
这次我们用一个二次方程来拟合一下这些数据。
方程我们定义为如下:
[hat(y_i)=W_1*x_i^2 + W_2*x_i+b
]
那么这样的话,我们就有三个参数 W_1, W_2, b。我们先给这三个参数一个初始数值。
w_1 = 1000
w_2 =1000
b = 1000
print(w_1)
print(w_2)
print(b)
y_pred = w_1* np.power(unrate['Year'],2) + w_2* unrate['Year'] + b
plt.scatter(unrate['Year'],unrate['Salary'])
plt.plot(unrate['Year'],y_pred)
plt.show()
1000
1000
1000
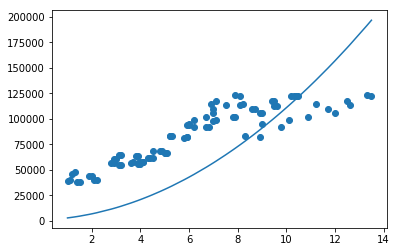
我们如果按照上述的模型,求出预测值(hat{y}),我们需要一个函数来评估这个值的好坏。
[loss=sum_{i=0}^{n} (y_i -hat{y}_i)^2
]
这个函数和一次的一样,没有任何变化。接下来,我们需要求出这个函数的导函数。
[frac{dl}{dw_1} = frac{dl}{dhat{y}}*frac{dhat{y}}{dw_1}
=-2sum_{i=0}^{n}(y_i-hat{y}_i)*x_i^2
]
[frac{dl}{dw_2} = frac{dl}{dhat{y}}*frac{dhat{y}}{dw_2}=-2sum_{i=0}^{n}(y_i-hat{y}_i)*x_i
]
[frac{dl}{db}=frac{dl}{dhat{y}}*frac{dhat{y}}{db}=-2sum_{i=0}^{n}(y_i-hat{y}_i)
]
我们来把上述的函数代码化
def train(w_1,w_2, b):
learning_rate = 0.000001
y_pred = w_1* np.power(unrate['Year'],2) + w_2* unrate['Year'] + b
dw_1 = -2*np.sum( np.transpose(unrate['Salary'] - y_pred)*np.power(unrate['Year'],2))
dw_2 = -2*np.sum( np.transpose(unrate['Salary'] - y_pred)*unrate['Year'])
db = -2*np.sum((unrate['Salary'] - y_pred))
temp_w_1 = w_1 - learning_rate * dw_1
temp_w_2 = w_2 - learning_rate * dw_2
temp_b = b - learning_rate * db
w_1 = temp_w_1
w_2= temp_w_2
b = temp_b
return w_1,w_2,b
我们来运行下测试下效果:
for i in range(10000):
w_1, w_2, b = train(w_1,w_2,b)
print(w_1)
print(w_2)
print(b)
y_pred = w_1 * np.power(unrate['Year'],2) + w_2 * unrate['Year'] + b
loss = np.power((y_pred-unrate['Salary']),2).sum()
plt.scatter(unrate['Year'],unrate['Salary'])
plt.plot(unrate['Year'],y_pred)
-695.3117280326662
17380.592541992835
8744.131370136933
8487947406.30475
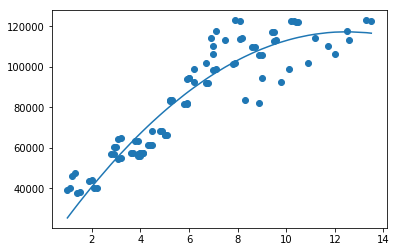
上面就是我们拟合出来的效果。
我们可以看出来,比我们之前一次的拟合的数据要好很多。