什么是算法:如何寻找稳定的婚姻搭配
引言 什么是算法
如何寻找稳定的婚姻搭配
据说,一本书开篇就直言不讳地谈起两性的话题,这本书准能畅销。有幸的是,在众多可以用来引入“算法”的话题中,我最喜欢的那一个还真与两性有那么一些关系。假如你是一个媒人,有若干个单身男子登门求助,还有同样多的单身女子也前来征婚。如果你已经知道这些女孩在每个男人心目中的排名,以及男孩们在每个女孩心中的排名(1),你应该怎样为他们牵线配对呢?
最好的配对方案当然是,每个人的另一半正好都是自己的“第一选择”。这虽然很完美,但绝大多数情况下都不可能实现。比方说,男 1 号的最爱是女 1 号,而女 1 号的最爱不是男 1 号,这两个人的最佳选择就不可能被同时满足。如果出现了好几个男人的最爱都是同一个女孩儿的情况,这几个男人的首选也不会同时得到满足。当这种最为理想的配对方案无法实现时,怎样的配对方案才能令人满意呢?
其实,找的对象太完美不见得是个好事儿,和谐才是婚姻的关键。如果男 1 号和女 1 号各自有各自的对象,但男 1 号觉得,比起自己现在的对象,女 1 号更好一些;女 1 号也发现,在自己心目中,男 1 号的排名比现男友更靠前一些。这样一来,这两人就可能会发生外遇,最后扔下各自现在的对象,一起私奔了——因为这个结果对他们两人都更好一些。在一种男女配对的方案中,如果出现了这种情况,我们就说婚姻搭配是不稳定的。作为一个红娘,你深深地知道,对象介绍得不好没有关系,就怕婚姻关系不稳定。给客户牵线配对时,虽然不能让每个人都得到最合适的,但婚姻搭配必须得是稳定的。换句话说,对于每一个人,在他心目中比他当前的伴侣更好的异性,都不会认为他也是一个更好的选择。现在,我们的问题就是:稳定的婚姻搭配总是存在吗?应该怎样寻找出一个稳定的婚姻搭配?
为了便于分析,我们下面做一些约定。我们用字母 A 、 B 、 C 对男性进行编号,用数字 1 、 2 、 3 对女性进行编号。我们把所有男性从上到下列在左侧,括号里的数字表示每个人心目中对所有女性的排名;再把所有女性列在右侧,用括号里的字母表示她们对男性的偏好。图 0-1 所示的就是有 2 男 2 女的一种情形,每个男的都更喜欢女 1 号,但女 1 号更喜欢男 B ,女 2 号更喜欢男 A 。若按 A-1 、 B-2 进行搭配,则男 B 和女 1 都更喜欢对方一些,这样的婚姻搭配就是不稳定的。但若换一种搭配方案(如图
0-2 ),这样的搭配就是稳定的了。

图 0-1 一个不稳定的婚姻搭配 男 B 和女 1 都不满意现任伴侣
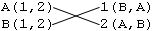
图 0-2 一个稳定的婚姻搭配
可能很多人会立即想到一种寻找稳定婚姻搭配的策略:不断修补当前搭配方案。如果两个人互相之间都觉得对方比自己当前的伴侣更好,就让这两个人成为一对,剩下被甩的那两个人组成一对。如果还有想要私奔的男女对,就继续按照他们的愿望对换情侣,直到最终消除所有的不稳定组合。容易看出,应用这种“修补策略”所得到的最终结果一定满足婚姻的稳定性,但这种策略的问题就在于,它不一定有一个“最终结果”。事实上,按照上述方法反复调整搭配方案,最终有可能会陷入一个死循环,因此该策略甚至不能保证得出一个确定的方案来。
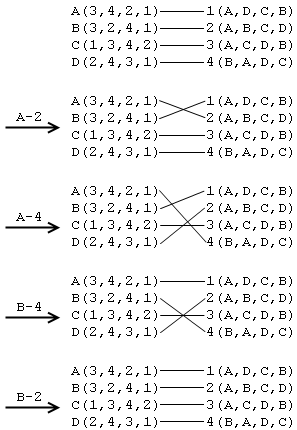
图 0-3 应用“修补策略”可能会产生死循环
1962 年,美国数学家 David Gale 和 Lloyd Shapley 发明了一种寻找稳定婚姻的策略。不管男女各有多少人,不管他们各自的偏好如何,应用这种策略后总能得到一个稳定的婚姻搭配。换句话说,他们证明了稳定的婚姻搭配总是存在的。有趣的是,这种策略反映了现实生活中的很多真实情况。
在这种策略中,男人将一轮一轮地去追求他中意的女子,女子可以选择接受或者拒绝她的追求者。第一轮,每个男人都选择自己名单上排在首位的女人,并向她表白。此时,一个女孩儿可能面对的情况有三种:没有人跟她表白,只有一个人跟她表白,有不止一个人跟她表白。在第一种情况下,这个女孩儿什么都不用做,只需要继续等待;在第二种情况下,接受那个人的表白,答应暂时和他做男女朋友;在第三种情况下,从所有追求者中选择自己最中意的那一位,答应和他暂时做男女朋友,并拒绝其他所有的追求者。
第一轮结束后,有些男人已经有女朋友了,有些男人仍然是单身。在第二轮追女行动中,每个单身男都从所有还没拒绝过他的女孩中选出自己最中意的那一个,并向她表白,不管她现在是否是单身。和第一轮一样,女孩儿们需要从表白者中选择最中意的一位,拒绝其他追求者。注意,如果这个女孩儿已经有男朋友了,当她遇到了更好的追求者时,她必须拒绝掉现在的男友,投向新的追求者的怀抱。这样,一些单身男人将会得到女友,那些已经有了女友的人也可能会被甩掉,重新变成光棍。在以后的每一轮中,单身的男人继续追求列表中的下一个女孩儿,女孩儿则从包括现男友在内的所有追求者中选择最好的一个,并对其他人说不。这样一轮一轮地进行下去,直到某个时候所有人都不再单身,下一轮将不会有任何新的表白发生,整个过程自动结束。此时的婚姻搭配就一定是稳定的了。
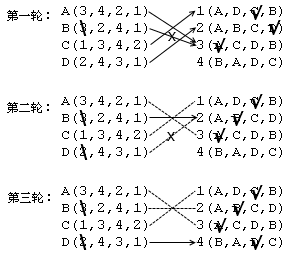
图 0-4 应用上述策略,三轮之后将得出稳定的婚姻搭配
这个策略会不会像之前的修补法一样,出现永远也无法终止的情况呢?不会。下面我们将说明,随着轮数的增加,总有一个时候所有人都能配上对。由于在每一轮中,至少会有一个男人向某个女人告白,因此总的告白次数将随着轮数的增加而增加。倘若整个流程一直没有因所有人都配上对了而结束的话,最终必然会出现某个男人追遍了所有女孩儿的情况。而一个女孩儿只要被人追过一次,以后就不可能再单身了。既然所有女孩儿都被这个男人追过,就说明所有女孩儿现在都不是单身,也就是说此时所有人都配上对了。
接下来,我们还需要证明,这样得出的配对方案确实是稳定的。首先注意到,随着轮数的增加,一个男人追求的对象总是越来越糟,而一个女孩儿的男友只可能变得越来越好。假设男 A 和女 1 各自有各自的对象,但比起现在的对象来,男 A 更喜欢女 1 。因此,在此之前男 A 肯定已经跟女 1 表白过。既然女 1 最后没有跟男 A 在一起,说明女 1 拒绝了男 A ,也就是说她有了比男 A 更好的男人。这就证明了,两个人虽然不是一对,但都觉得对方比自己现在的伴侣好,这样的情况绝不可能发生。
我们把用来解决某种问题的一个策略,或者说一个方案,或者说一个处理过程,或者说一系列操作规则,或者更贴切的,一套计算方法,叫做“算法”。上面这个用来寻找稳定婚姻的策略就叫做“ Gale-Shapley 算法”,有些人也管它叫“延迟认可算法”。
每个算法都有它的实际意义,能给我们带来很多启发。 Gale-Shapley 算法最大的意义就在于,作为一个为这些男女牵线的媒人,你并不需要亲自计算稳定婚姻匹配,甚至根本不需要了解每个人的偏好,只需要按照这个算法组织一个男女配对活动就可以了。你需要做的仅仅是把算法流程当作游戏规则告诉大家,游戏结束后会自动得到一个大家都满意的婚姻匹配。对于男性来说,从最喜欢的女孩儿开始追起是顺理成章的事;对于女性来说,不断选择最好的男人也正好符合她的利益。因此,大家会自动遵守游戏规则,不用担心有人虚报自己的偏好。
历史上,这样的“配对游戏”还真有过实际应用,并且更有意思的是,这个算法的应用居然比算法本身的提出还早 10 年。早在 1952 年,美国就开始用这种办法给医学院的学生安排工作,这被称之为“全国住院医师配对项目”。配对的基本流程就是,各医院从尚未拒绝这一职位的医学院学生中选出最佳人选并发送聘用通知,当学生收到来自各医院的聘用通知后,系统会根据他所填写的意愿表自动将其分配到意愿最高的职位,并拒绝掉其它的职位。如此反复,直到每个学生都分配到了工作。当然,那时人们并不知道这样的流程可以保证工作分配的稳定性,只是凭直觉认为这是很合理的。直到
10 年之后, Gale 和 Shapley 才系统地研究了这个流程,提出了稳定婚姻问题,并证明了这个算法的正确性。
用稳定性来评价配对方案的好坏的确很站得住脚,但有时候我们也会遇到一些别的需求,它们又对应着算法世界中的诸多其它问题。比方说,如果我们已经知道每一对男女之间的“相配度”,如何寻找一种配对方案使得由此产生的总相配度最大?在算法领域中,这被称为二分图的最大权值匹配问题。再比如,如果不考虑性别的差异(比如同桌、搭档的匹配),问题就更加复杂了,这通常被归入一般图匹配的范畴。这些问题现在都已经找到了有效的算法,不过它们太复杂,已经超出本书的范围了。生活中的算法应用随处可见。这本书要做的,就是带领大家从身边熟悉的事物出发,一睹算法的无尽魅力。
——————————————————————-
(1) 这个排名的来源并不重要,它有可能是客户根据每位异性的个人资料直接给出的,也有可能是通过客户提交的个人信息推算出来的。
源自:点击打开链接