一、概念:KNN(K Near Neighbor):K个最近的邻居,即每个样本都可以用它最接近的K个邻居来代表。

当k=1时,?可以用红方块代表,因为k=1时,方块离?最近
当k=5时,?可以用三角代表,因为k=5时,5个离?最近的图片中,有三个是三角,少数服从多数,所以可以用三角代表
二、判别方法
1、计算已知类别数据集中的点与当前点之间的距离
2、按距离递增次序排序
3、选取当前点距离最小的K个点
4、统计前k个点所在类别出现的概率
5、返回前k个点出现频率最高的类别作为当前点的预测类别
三、例题

1、根据欧式距离公式计算出《唐人街探案》各特征和其它影片各特征之间的距离

算出所有距离:
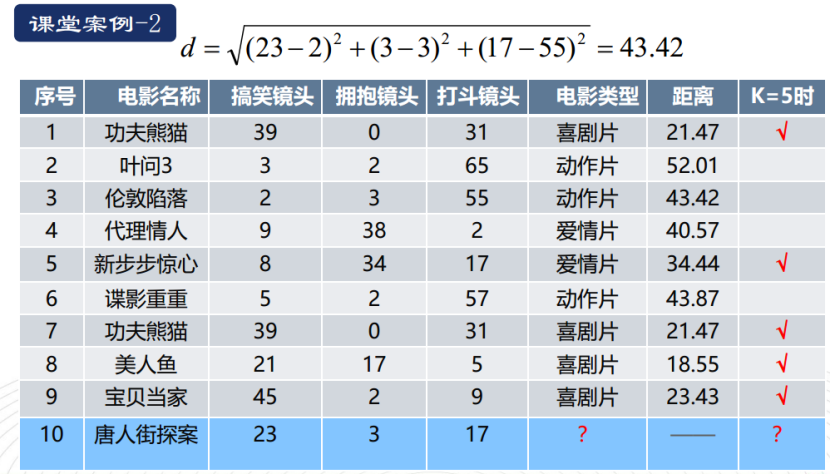
取k=5时,按递增排序,前4个电影都是喜剧片,有一个是爱情片,所以《唐人街探案》属于喜剧片
四、KNN特点
1、优点:简单有效、重新训练的代价低、算法复杂度低、适合类域交叉样本、适用大样本自动分类
2、缺点:惰性学习、类别分类不标准化、输出解释性不强、不均衡性、计算量大
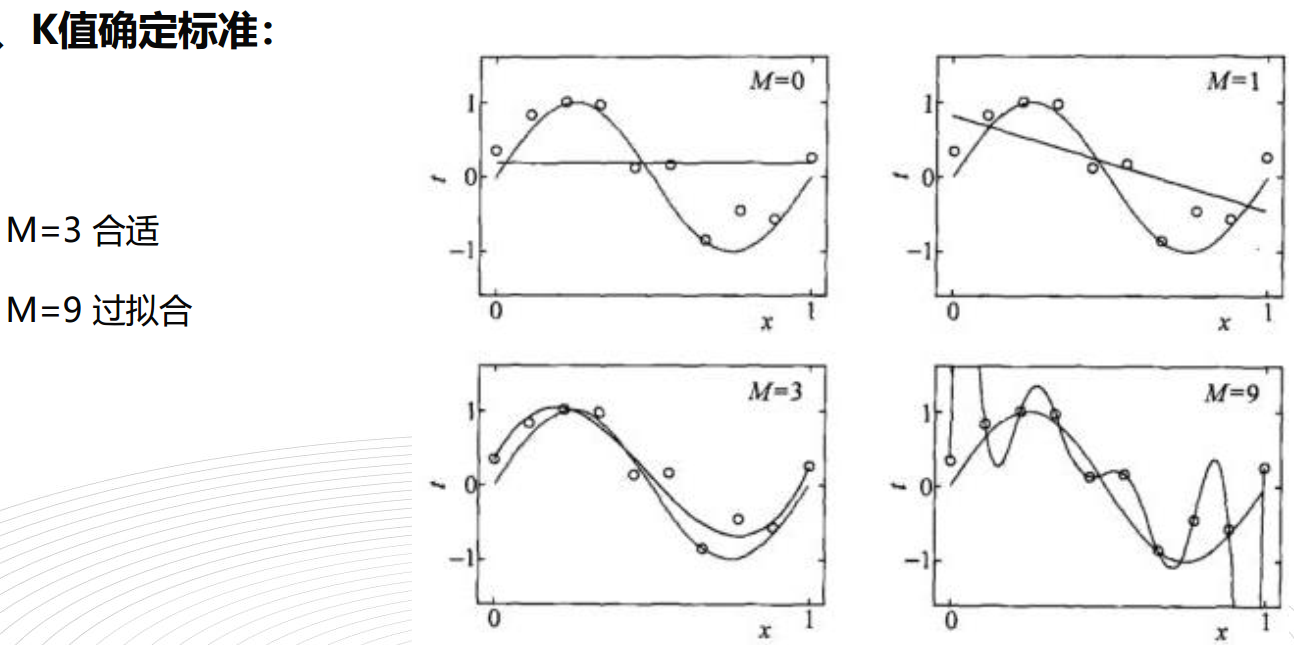
过拟合:什么都学,主要的和次要的都学,把次要的当成主要的学,没有重点
欠拟合:基本的特征都没学会
K值选择会对KNN的结果产生重大影响
如果选择较小的k值,就相当于用较小的领域中的训练实例进行预测,“学习”的近似误差会减小,只有输入实例较近的训练实例才会对预测结果起作用。但缺点是“学习”的估计误差会增大,预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声,预测就会出错。换句话说,k值的减小就意味着整体模型变得复杂,容易发生过拟合。
如果选择较大的k值,就相当于用较大领域中训练实例进行预测,其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大,这里与输入实例较远的(不相似的)训练实例也会对预测起作用,使预测发生错误,k值的增大就意味着整体的模型变得简单。
如果k=N,那么无论输入实例是什么,都将简单地预测它属于在训练实例中最多的类,这里,模型过于简单,完全忽略训练实例中的大量有用停下,是不可取的
在应用中,k值一般取一个比较小的数值,通常采用交叉验证法来选取最优的k值