51. N皇后
题目描述
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
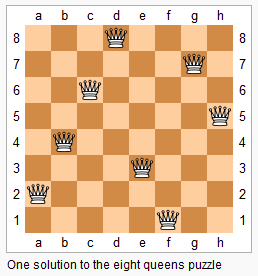
上图为 8 皇后问题的一种解法。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例
输入: 4
输出: [
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。
思路
首先,明确皇后所能攻击的格子是它自身所在格子的行、列、斜(撇)和反斜(捺)。
所以,一个可能的放置方法如下图所示:
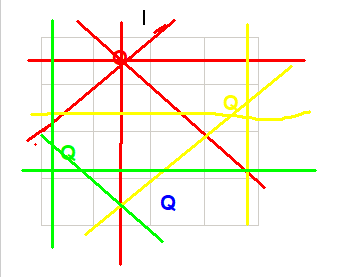
关键:判断格子是否能放皇后。转换成程序语言就是判断该格子是否满足相应条件。通过观察可以发现撇的行列下标相加为常数,捺的行列下标相减为常数。
因此有以下代码:
class Solution(object):
def solveNQueens(self, n):
"""
:type n: int
:rtype: List[List[str]]
"""
if n < 1:
return []
self.result = []
self.cols = set()
self.pie = set()
self.na = set()
self.DFS(n, 0, [])
return self._generate_result(n)
def DFS(self, n, row, cur_state):
if row >= n:
self.result.append(cur_state)
return
for col in range(n):
if col in self.cols or row + col in self.pie or row - col in self.na:
# 在攻击范围内,不能放
continue
self.cols.add(col)
self.pie.add(row + col)
self.na.add(row - col)
self.DFS(n, row + 1, cur_state + [col])
self.cols.remove(col)
self.pie.remove(row + col)
self.na.remove(row - col)
# 用来生成所要求的输出形式
def _generate_result(self, n):
board = []
for res in self.result:
for i in res:
board.append("." * i + "Q" + "." * (n - i - 1))
return [board[i: i + n] for i in range(0, len(board), n)]
同样的思路,来观摩下大神的写法:
class Solution(object):
def solveNQueens(self, n):
"""
:type n: int
:rtype: List[List[str]]
"""
def DFS(queens, xy_dif, xy_sum):
p = len(queens)
if p == n:
result.append(queens)
return None
for q in range(n):
if q not in queens and p-q not in xy_dif and p+q not in xy_sum:
DFS(queens+[q], xy_dif+[p-q], xy_sum+[p+q])
result = []
DFS([], [], [])
return [["."*i + "Q" + "."*(n-i-1) for i in sol] for sol in result]
其中 xy_dif 就是我们的捺, xy_sum 就是我们的撇。
GitHub地址:https://github.com/protea-ban/LeetCode
