算法初级面试题04——递归/非递归遍历二叉树、直观打印二叉树、寻找后继前驱节点、序列化/反序列化、折纸问题、判断是否平衡/搜索/完全二叉树、求完全二叉的节点数

 今天主要讨论：二叉树相关内容

题目一

实现二叉树的先序、中序、后序遍历，包括递归方式和非递归方式

 

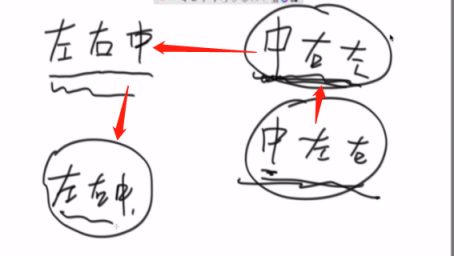
先序遍历 头左右，右图遍历顺序

   

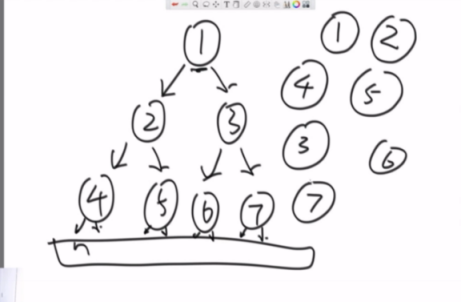
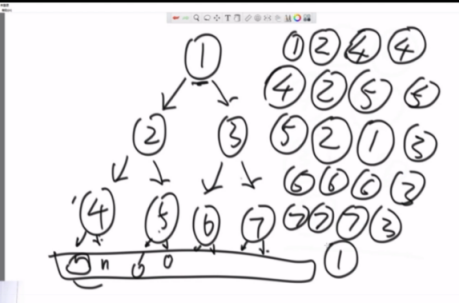
如果打印时机放在第一次来到这个节点的时候，就是先序遍历。

    public static void preOrderRecur(Node head) {
        if (head == null) {
            return;
        }
        System.out.print(head.value + " ");
        preOrderRecur(head.left);
        preOrderRecur(head.right);
    }

如果放在第二次来到这个节点的时候，就是中序遍历。

    public static void inOrderRecur(Node head) {
        if (head == null) {
            return;
        }
        inOrderRecur(head.left);
        System.out.print(head.value + " ");
        inOrderRecur(head.right);
    }

如果把打印时机放在第三次来点这个节点的时候，就是后序遍历。

    public static void posOrderRecur(Node head) {
        if (head == null) {
            return;
        }
        posOrderRecur(head.left);
        posOrderRecur(head.right);
        System.out.print(head.value + " ");
    }

主要是打印时机放在哪里。就被加工出了先序中序后序。

非递归（先序）：

中间在最前面，先压right再压left

因为二叉树只能一直往下走，那就要想一个能回去的结构，栈机结构就很合适。

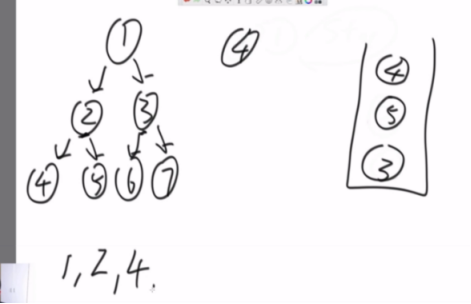
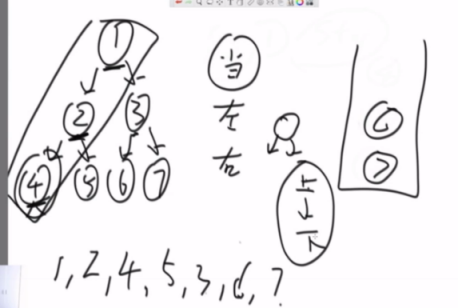
    public static void preOrderUnRecur(Node head) {
        System.out.print("pre-order: ");
        if (head != null) {
            Stack<Node> stack = new Stack<Node>();
            stack.add(head);
            while (!stack.isEmpty()) {
                head = stack.pop();
                System.out.print(head.value + " ");
                if (head.right != null) {
                    stack.push(head.right);
                }
                if (head.left != null) {
                    stack.push(head.left);
                }
            }
        }
        System.out.println();
    }

非递归（中序）：左中右

整棵树是可以被左边界分解的（弹出顺序是左中）。逆序去处理的过程，实际上可以把整棵树都打印出来。回到2的时候，又把2的右树进行左边界分解，所以你懂得，在分解的时候也不耽误打印整棵树。

  

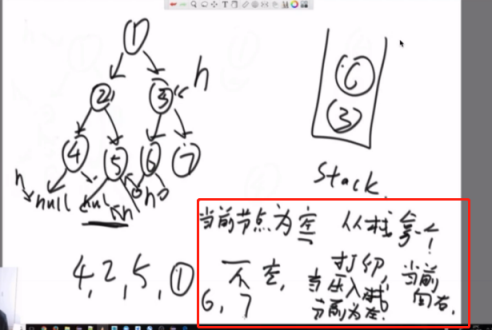
    public static void inOrderUnRecur(Node head) {
        System.out.print("in-order: ");
        if (head != null) {
            Stack<Node> stack = new Stack<Node>();
            while (!stack.isEmpty() || head != null) {
                if (head != null) {//当前节点把左边界都压栈
                    stack.push(head);
                    head = head.left;
                } else {//当前节点为空，从栈中弹出一个打印
                    head = stack.pop();
                    System.out.print(head.value + " ");
                    head = head.right;//向右走
                }
            }
        }
        System.out.println();
    }

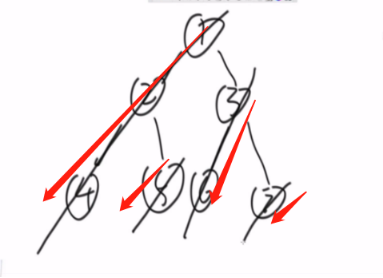
非递归（后序）：左右中

递归会返回一个节点三次，而栈会返回两次，后序遍历需要在返回第三次的时候打印。

修改先序遍历，这次先压入左子树，形成中右左，再利用一个辅助栈，把打印结果逆序打印，即是答案。

 

    public static void posOrderUnRecur1(Node head) {
        System.out.print("pos-order: ");
        if (head != null) {
            Stack<Node> s1 = new Stack<Node>();
            Stack<Node> s2 = new Stack<Node>();
            s1.push(head);
            while (!s1.isEmpty()) {
                head = s1.pop();
                s2.push(head);//本来先序的话是直接输出的，但是这里后序为了左右中输出，就先把中右左存在临时栈中
                if (head.left != null) {
                    s1.push(head.left);
                }
                if (head.right != null) {
                    s1.push(head.right);
                }
            }
            while (!s2.isEmpty()) {
                System.out.print(s2.pop().value + " ");
            }
        }
        System.out.println();
    }

极客写法：只使用一个栈

    public static void posOrderUnRecur2(Node h) {
        System.out.print("pos-order: ");
        if (h != null) {
            Stack<Node> stack = new Stack<Node>();
            stack.push(h);
            Node c = null;
            while (!stack.isEmpty()) {
                c = stack.peek();
                if (c.left != null && h != c.left && h != c.right) {
                    stack.push(c.left);
                } else if (c.right != null && h != c.right) {
                    stack.push(c.right);
                } else {
                    System.out.print(stack.pop().value + " ");
                    h = c;
                }
            }
        }
        System.out.println();
    }

题目二

如何直观的打印一颗二叉树

 

一个福利函数，用于调试二叉树。

 

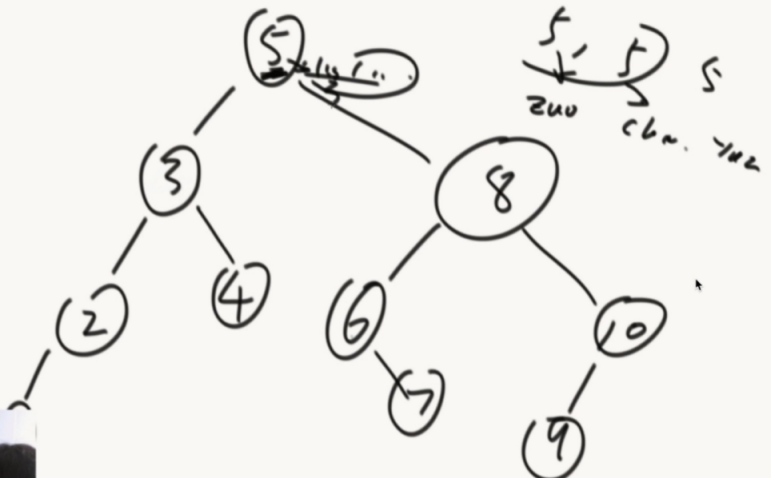
H1H表示1是头结点，v66v是向下指的，他的父节点是左下方离他最近的

^555555^是向上指的，父节点为左上距离最近的。

public class Code_02_PrintBinaryTree {

    public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int data) {
            this.value = data;
        }
    }

    public static void printTree(Node head) {
        System.out.println("Binary Tree:");
        printInOrder(head, 0, "H", 17);
        System.out.println();
    }

    public static void printInOrder(Node head, int height, String to, int len) {
        if (head == null) {
            return;
        }
        printInOrder(head.right, height + 1, "v", len);
        String val = to + head.value + to;
        int lenM = val.length();
        int lenL = (len - lenM) / 2;
        int lenR = len - lenM - lenL;
        val = getSpace(lenL) + val + getSpace(lenR);
        System.out.println(getSpace(height * len) + val);
        printInOrder(head.left, height + 1, "^", len);
    }

    public static String getSpace(int num) {
        String space = " ";
        StringBuffer buf = new StringBuffer("");
        for (int i = 0; i < num; i++) {
            buf.append(space);
        }
        return buf.toString();
    }

    public static void main(String[] args) {
        Node head = new Node(1);
        head.left = new Node(-222222222);
        head.right = new Node(3);
        head.left.left = new Node(Integer.MIN_VALUE);
        head.right.left = new Node(55555555);
        head.right.right = new Node(66);
        head.left.left.right = new Node(777);
        printTree(head);

        head = new Node(1);
        head.left = new Node(2);
        head.right = new Node(3);
        head.left.left = new Node(4);
        head.right.left = new Node(5);
        head.right.right = new Node(6);
        head.left.left.right = new Node(7);
        printTree(head);

        head = new Node(1);
        head.left = new Node(1);
        head.right = new Node(1);
        head.left.left = new Node(1);
        head.right.left = new Node(1);
        head.right.right = new Node(1);
        head.left.left.right = new Node(1);
        printTree(head);

    }

}

题目三

在二叉树中找到一个节点的后继节点

【题目】 现在有一种新的二叉树节点类型如下：

public class Node {

　　public int value;

　　public Node left;

　　public Node right;

　　public Node parent;

　　public Node(int data) { this.value = data; }

}

该结构比普通二叉树节点结构多了一个指向父节点的parent指针。假设有一棵Node类型的节点组成的二叉树，树中每个节点的parent指针都正确地指向自己的父节点，头节点的parent指向null。只给一个在二叉树中的某个节点 node，请实现返回node的后继节点的函数。

在二叉树的中序遍历的序列中，node的下一个节点叫作node的后继节点。

 

中序遍历的顺序。（前继和后继节点）

 

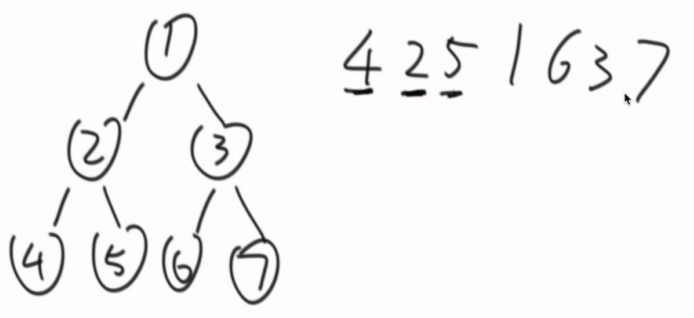
怎么避免遍历整棵树，也能找到后继节点？

规律：x节点，如果有右子树，那么他的后继节点是右子树上最左的节点。（根据遍历顺序左中右，右子树后下一个遍历的就是左）

当x没有右子树，要找哪一个结点的左子树是以x结尾的。

通过x的父指针找到父结点，如果发现x是右孩子，就继续往上，一直到某一节点，是他父结点的左孩子，停止。（注意最右边的7找到的是null，代码层面要做相应的判断）

    

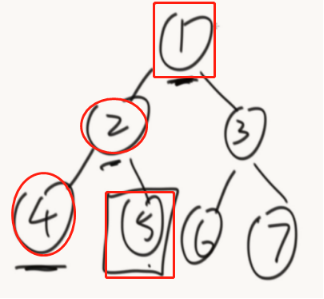
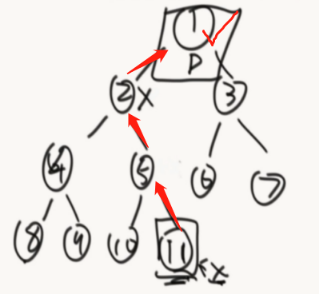
public class Code_03_SuccessorNode {

    public static class Node {
        public int value;
        public Node left;
        public Node right;
        public Node parent;

        public Node(int data) {
            this.value = data;
        }
    }

    public static Node getSuccessorNode(Node node) {
        if (node == null) {
            return node;
        }
        if (node.right != null) {//如果有右子树
            return getLeftMost(node.right);
        } else {//如果没有右子树
            Node parent = node.parent;
            while (parent != null && parent.left != node) {
                node = parent;
                parent = node.parent;
            }
            return parent;
        }
    }

    //获得最左边的节点
    public static Node getLeftMost(Node node) {
        if (node == null) {
            return node;
        }
        while (node.left != null) {
            node = node.left;
        }
        return node;
    }

    public static void main(String[] args) {
        Node head = new Node(6);
        head.parent = null;
        head.left = new Node(3);
        head.left.parent = head;
        head.left.left = new Node(1);
        head.left.left.parent = head.left;
        head.left.left.right = new Node(2);
        head.left.left.right.parent = head.left.left;
        head.left.right = new Node(4);
        head.left.right.parent = head.left;
        head.left.right.right = new Node(5);
        head.left.right.right.parent = head.left.right;
        head.right = new Node(9);
        head.right.parent = head;
        head.right.left = new Node(8);
        head.right.left.parent = head.right;
        head.right.left.left = new Node(7);
        head.right.left.left.parent = head.right.left;
        head.right.right = new Node(10);
        head.right.right.parent = head.right;

        Node test = head.left.left;
        System.out.println(test.value + " next: " + getSuccessorNode(test).value);
        test = head.left.left.right;
        System.out.println(test.value + " next: " + getSuccessorNode(test).value);
        test = head.left;
        System.out.println(test.value + " next: " + getSuccessorNode(test).value);
        test = head.left.right;
        System.out.println(test.value + " next: " + getSuccessorNode(test).value);
        test = head.left.right.right;
        System.out.println(test.value + " next: " + getSuccessorNode(test).value);
        test = head;
        System.out.println(test.value + " next: " + getSuccessorNode(test).value);
        test = head.right.left.left;
        System.out.println(test.value + " next: " + getSuccessorNode(test).value);
        test = head.right.left;
        System.out.println(test.value + " next: " + getSuccessorNode(test).value);
        test = head.right;
        System.out.println(test.value + " next: " + getSuccessorNode(test).value);
        test = head.right.right; // 10's next is null
        System.out.println(test.value + " next: " + getSuccessorNode(test));
    }

}

前驱怎么找？

x如果有左子树，就是左子树最右的节点。

如果x没有左子树，往上找，找到一个父结点的右孩子，是当前节点就停。

    public static Node getPrecursorNode(Node node){
        if (node == null) {
            return node;
        }
        if(node.left != null){
            return getRightMost(node);
        }else{
            Node parent = node.parent;
            while(parent!=null&& parent.right!=node){
                node = parent;
                parent = node.parent;
            }
            return parent;
        }
    }

    //获得最右边的节点
    public static Node getRightMost(Node node) {
        if (node == null) {
            return node;
        }
        while (node.right != null) {
            node = node.right;
        }
        return node;
    }

面试流程

一般亚马逊、谷歌、微软公司，4~5面。

 

要达到，面试官准备给你的题库全彻底完成。

3面4面就是技术面了，比方说设计一个系统停车场系统、图书馆系统

 

如果题目做完，需要问问面试官还有没有题目。万无一失

题目四

介绍二叉树的序列化和反序列化

 

怎么把信息保存成文件形式，以确保下次可以重建一棵树。

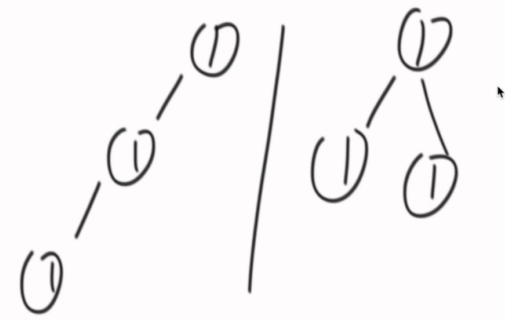
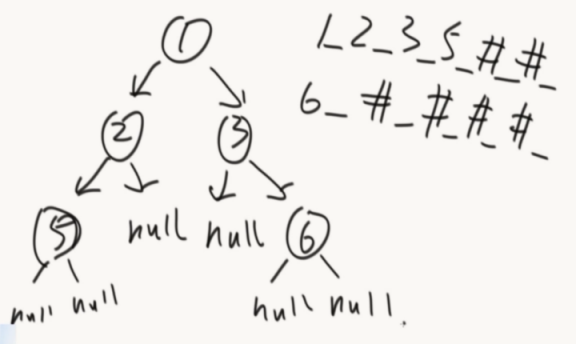
第一种：先序的方式序列化，树怎么变字符串，#表示遇到空

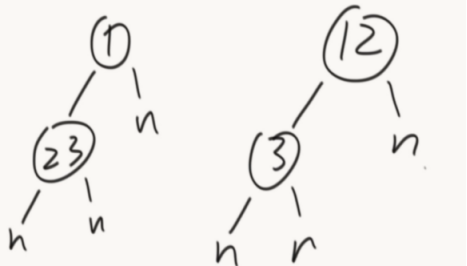
需要#和_是因为能更好的表示一些特殊的结构。

 

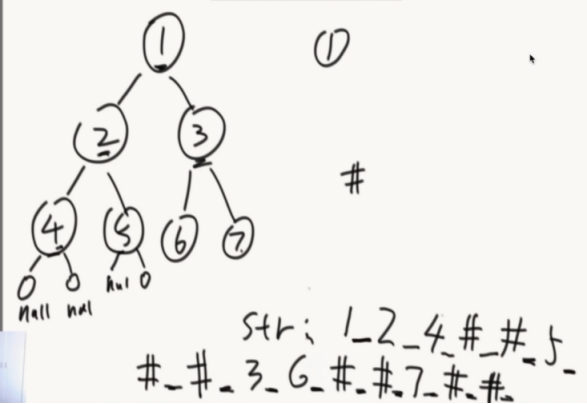
 留下划线的原因是为了识别以下的树形结构：

    public static String serialByPre(Node head) {
        if (head == null) {
            return "#_";
        }
        String res = head.value + "_";
        res += serialByPre(head.left);
        res += serialByPre(head.right);
        return res;
    }

怎么反序列化：怎么序列化的就怎么反序列化

利用_分隔，获得就是每一个节点，利用先序遍历的方式，反序列化

按照中左右的方式，依次建立。碰到空就不为空建立子树，返回父节点建立其他子树。（中序、后序同理）

 

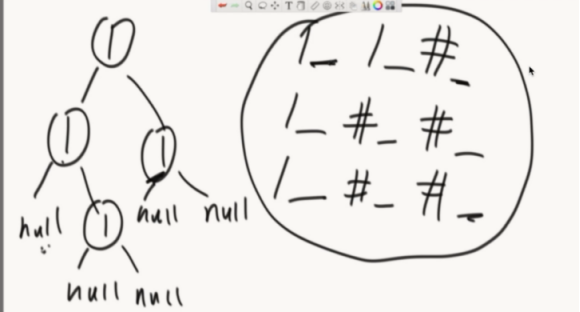
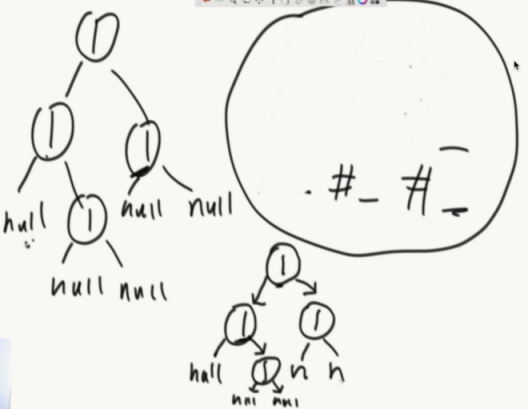
    public static Node reconByPreString(String preStr) {
        String[] values = preStr.split("_");
        Queue<String> queue = new LinkedList<String>();
        //加入到队列中
        for (int i = 0; i != values.length; i++) {
            queue.offer(values[i]);
        }
        return reconPreOrder(queue);
    }

    public static Node reconPreOrder(Queue<String> queue) {
        String value = queue.poll();
        if (value.equals("#")) {
            return null;
        }
        //中左右
        Node head = new Node(Integer.valueOf(value));
        head.left = reconPreOrder(queue);
        head.right = reconPreOrder(queue);
        return head;
    }

OJ测试就是通过把你的二叉树序列化，再和正确答案比对来判断是否正确的。牛客网就是按照层来序列化。

 

按层序列化同理：

 

    public static String serialByLevel(Node head) {
        if (head == null) {
            return "#_";
        }
        String res = head.value + "_";
        Queue<Node> queue = new LinkedList<Node>();
        queue.offer(head);
        while (!queue.isEmpty()) {
            head = queue.poll();
            if (head.left != null) {
                res += head.left.value + "_";
                queue.offer(head.left);
            } else {
                res += "#_";
            }
            if (head.right != null) {
                res += head.right.value + "_";
                queue.offer(head.right);
            } else {
                res += "#_";
            }
        }
        return res;
    }

    public static Node reconByLevelString(String levelStr) {
        String[] values = levelStr.split("_");
        int index = 0;
        Node head = generateNodeByString(values[index++]);
        Queue<Node> queue = new LinkedList<Node>();
        if (head != null) {
            queue.offer(head);
        }
        Node node = null;
        while (!queue.isEmpty()) {
            node = queue.poll();
            node.left = generateNodeByString(values[index++]);
            node.right = generateNodeByString(values[index++]);
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
        return head;
    }

    public static Node generateNodeByString(String val) {
        if (val.equals("#")) {
            return null;
        }
        return new Node(Integer.valueOf(val));
    }

题目五

折纸问题（福利课讲的）

【题目】 请把一段纸条竖着放在桌子上，然后从纸条的下边向上方对折1次，压出折痕后展开。此时 折痕是凹下去的，即折痕突起的方向指向纸条的背面。如果从纸条的下边向上方连续对折2 次，压出折痕后展开，此时有三条折痕，从上到下依次是下折痕、下折痕和上折痕。

给定一 个输入参数N，代表纸条都从下边向上方连续对折N次，请从上到下打印所有折痕的方向。 例如：N=1时，打印： down N=2时，打印： down down up

参考：https://blog.csdn.net/zhou_209/article/details/79437262

题目六

判断一棵二叉树是否是平衡二叉树

 

在树中任何一个节点，它左子树和右子树的高度差不超过一，这叫平衡二叉树。抛出一个套路：递归函数很好用，可以回到一个三次。

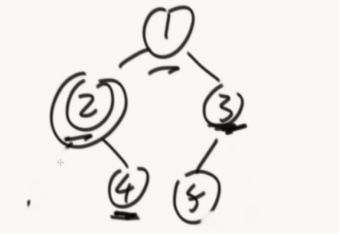
四个信息：左/右是否平衡、左/右的高

所以经过分析每颗子树应该返回，是否平衡和树高的信息。

下面就是码代码阶段：

难度在于要列出可能性。写代码的过程高度套路化。

列出可能性、整理出返回值的类型、整个递归过程按照同样的结构、得到子树的信息、整合子树的信息、加工出我的信息、往上返回、要求结构完全一致，因为是递归函数。

    public static class ReturnData{
        public boolean isBalance;
        public int level;

        public ReturnData(boolean isBalance, int level) {
            this.isBalance = isBalance;
            this.level = level;
        }
    }

    public static ReturnData process(Node head){
        if(head == null){
            return new ReturnData(true,0);
        }
        //如果左子树或者右子树返回了他们不是平衡的，那总体也不会是平衡的
        ReturnData lRData = process(head.left);
        if(!lRData.isBalance){
            return new ReturnData(true,0);
        }
        ReturnData rRData = process(head.right);
        if(!rRData.isBalance){
            return new ReturnData(true,0);
        }
        if(Math.abs(lRData.level - rRData.level) > 1){
            return new ReturnData(true,0);
        }
        return new ReturnData(true,Math.max(lRData.level,rRData.level)+1);
    }

你就想我们会遍历每个节点，我考虑以每个节点为头的整棵树，怎么怎么样都判断完，那么我整个答案就出来了。

这个大套路，整个方法论就这个过程。

左树收集什么信息，右树收集什么信息，列出可能性，这是你要去想的。

高度怎么变化的？

 

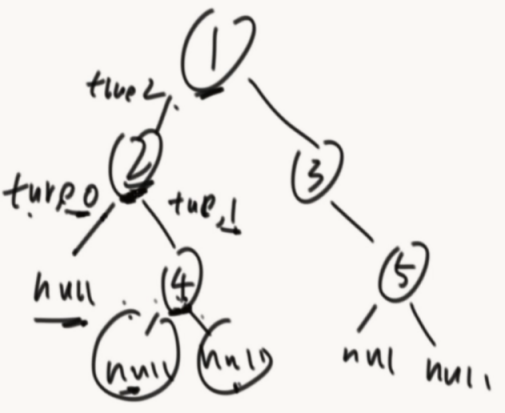
public class Code_06_IsBalancedTree {

    public static class Node {
                ...
    }

    public static boolean isBalance(Node head) {
        boolean[] res = new boolean[1];
        res[0] = true;
        getHeight(head, 1, res);
        return res[0];
    }

    public static int getHeight(Node head, int level, boolean[] res) {
        if (head == null) {
            return level;
        }
        int lH = getHeight(head.left, level + 1, res);
        if (!res[0]) {
            return level;
        }
        int rH = getHeight(head.right, level + 1, res);
        if (!res[0]) {
            return level;
        }
        if (Math.abs(lH - rH) > 1) {
            res[0] = false;
        }
        return Math.max(lH, rH);
    }

    public static void main(String[] args) {
        Node head = new Node(1);
        head.left = new Node(2);
        head.right = new Node(3);
        head.left.left = new Node(4);
        head.left.right = new Node(5);
        head.right.left = new Node(6);
        head.right.right = new Node(7);

        System.out.println(isBalance(head));

    }

}
                    

具体想进阶参考：树形DP

平衡二叉树用于解决效率的问题。

 

题目七

判断一棵树是否是搜索二叉树、判断一棵树是否是完全二叉树

搜索二叉树：左子树比他小，右子树比他大

中序遍历依次升序的就是。（通常来讲不出现重复节点，重复的话可以压缩在同一个list里面）

 

 

代码实现通过修改非递归的中序遍历来判断（对比之前的数和显示的数是否呈现出升序）（递归版怎么改？难度比较大）

    public static boolean isBST(Node head) {
        if (head == null) {
            return true;
        }
        Stack<Node> stack = new Stack<Node>();
        //首先有一个很小的数做初始值
        int flag = Integer.MIN_VALUE;
        while (!stack.isEmpty() || head != null) {
            if (head != null) {
                stack.push(head);
                head = head.left;
            } else {
                head = stack.pop();
                if (head.value < flag) {
                    return false;//不是升序就不是搜索二叉树
                }
                head = head.right;
            }
        }
        return true;
    }

    //Morris遍历版本
    //左子树小、右子树大
    public static boolean isBST(Node head) {
        if (head == null) {
            return true;
        }
        boolean res = true;
        Node pre = null;
        Node cur1 = head;
        Node cur2 = null;
        while (cur1 != null) {
            cur2 = cur1.left;
            if (cur2 != null) {
                while (cur2.right != null && cur2.right != cur1) {
                    cur2 = cur2.right;
                }
                if (cur2.right == null) {
                    cur2.right = cur1;
                    cur1 = cur1.left;
                    continue;
                } else {
                    cur2.right = null;
                }
            }
            if (pre != null && pre.value > cur1.value) {
                res = false;
            }
            pre = cur1;
            cur1 = cur1.right;
        }
        return res;
    }

完全二叉树怎么判断？

按层遍历，以下条件按照顺序判断

1、如果一个子树有右孩子没左孩子肯定不是完二叉。返回false

2、如果一个节点，不是左右孩子都全，出现这种情况，他后面出现的节点，都必须是叶子节点，否则false。

State状态一开始是false，遇到二的情况变true，遇到后续节点不是叶子节点就直接返回false

 

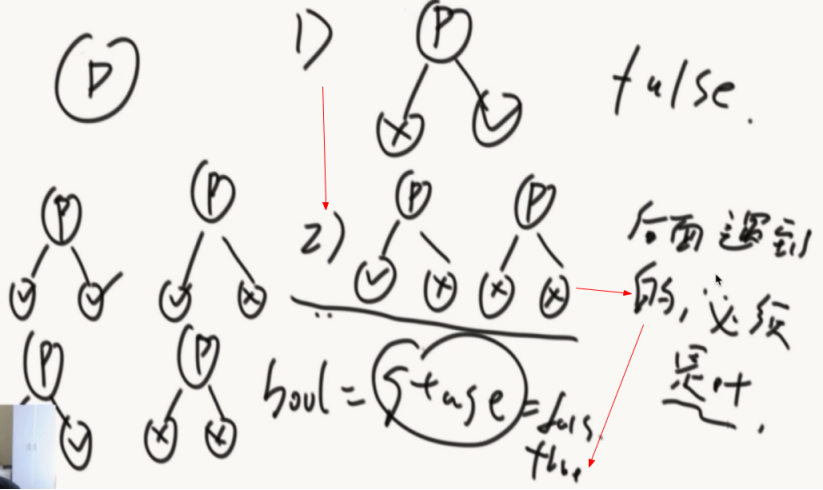
节点5中了第二种情况，接下来的都要是叶子节点。

 

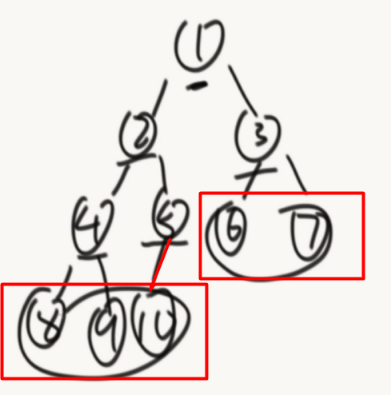
    public static boolean isCBT(Node head) {
        if (head == null) {
            return true;
        }
        Queue<Node> queue = new LinkedList<Node>();
        boolean leaf = false;
        Node l = null;
        Node r = null;
        queue.offer(head);
        while (!queue.isEmpty()) {
            head = queue.poll();
            l = head.left;
            r = head.right;
            if ((leaf && (l != null || r != null)) || (l == null && r != null)) {
                return false;
            }
            if (l != null) {
                queue.offer(l);
            }
            if (r != null) {
                queue.offer(r);
            } else {//如果右子树为空，左子树不为空，接下来的都要是叶子节点
                leaf = true;
            }
        }
        return true;
    }

DQ和Q都可以使用双端链表来实现。（Java中的LinkedList底层实现）

 

题目八

已知一棵完全二叉树，求其节点的个数

要求：时间复杂度低于O(N)，N为这棵树的节点个数

先遍历左边界，获得层高。然后遍历右子树的左边界，如果等于总的左边界的层高，就证明，左子树是满二叉树。

然后通过公式计算出左子树的个数，再递归处理右子树。

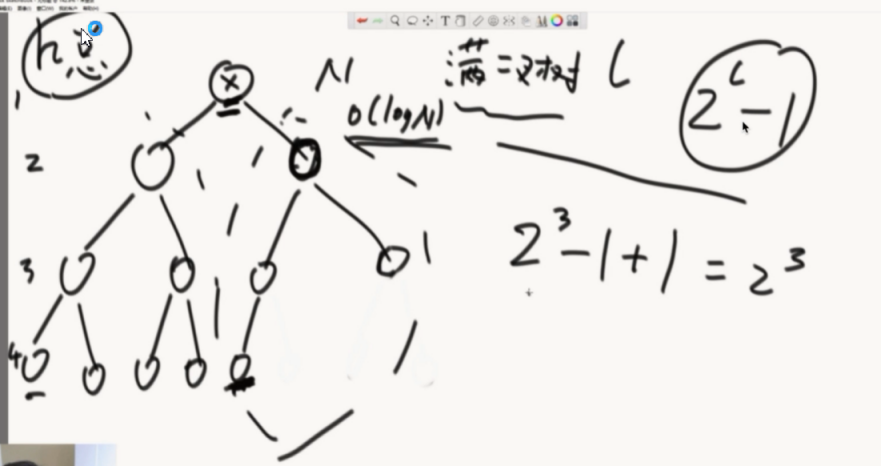
如果右子树的左边界没到最后一层。那就证明，右子树是左树高度-1的满二叉树。然后再递归处理左树。

所以每次拿到一个节点，就判断右树的左边界是否到最后一层，到了左树就是满的，没到右树就是满的，只不过左树和右树满的高度不一样而已，都可以使用公式来计算。剩下的节点递归去求。

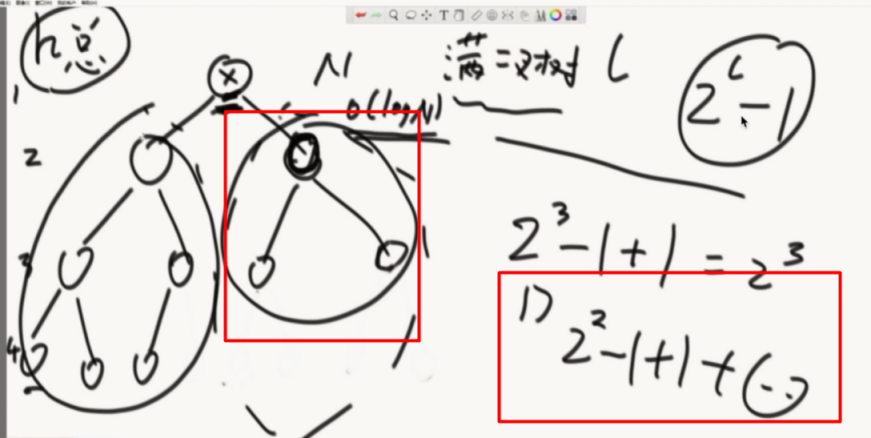
代码解说：

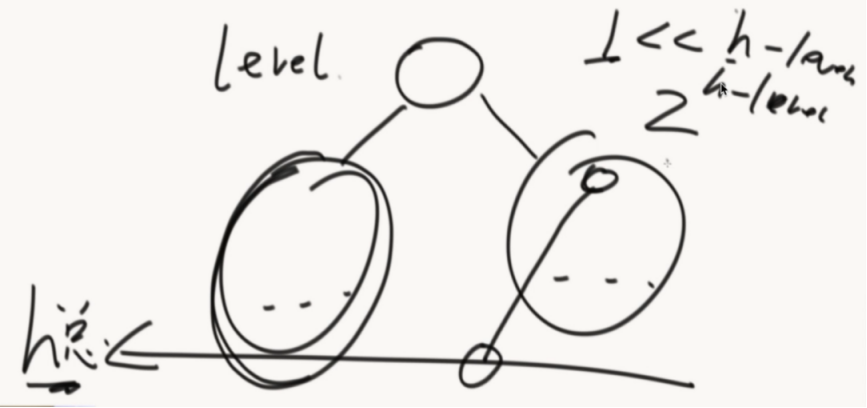
public class Code_08_CompleteTreeNodeNumber {

    public static class Node {
        ...
    }

    public static int nodeNum(Node head) {
        if (head == null) {
            return 0;
        }
        return bs(head, 1, mostLeftLevel(head, 1));
    }
    //当前节点、节点在第几层、整棵树的树高
    public static int bs(Node node, int level, int h) {
        if (level == h) {//如果level来到最后一层，就是叶子节点
            return 1;
        }
        if (mostLeftLevel(node.right, level + 1) == h) {
            return (1 << (h - level)) + bs(node.right, level + 1, h);
        } else {
            return (1 << (h - level - 1)) + bs(node.left, level + 1, h);
        }
    }

    public static int mostLeftLevel(Node node, int level) {
        while (node != null) {
            level++;
            node = node.left;
        }
        return level - 1;
    }

    public static void main(String[] args) {
        Node head = new Node(1);
        head.left = new Node(2);
        head.right = new Node(3);
        head.left.left = new Node(4);
        head.left.right = new Node(5);
        head.right.left = new Node(6);
        System.out.println(nodeNum(head));

    }

}

算法复杂度：

遍历节点 logN   获得左边界 LogN    LogN²

 

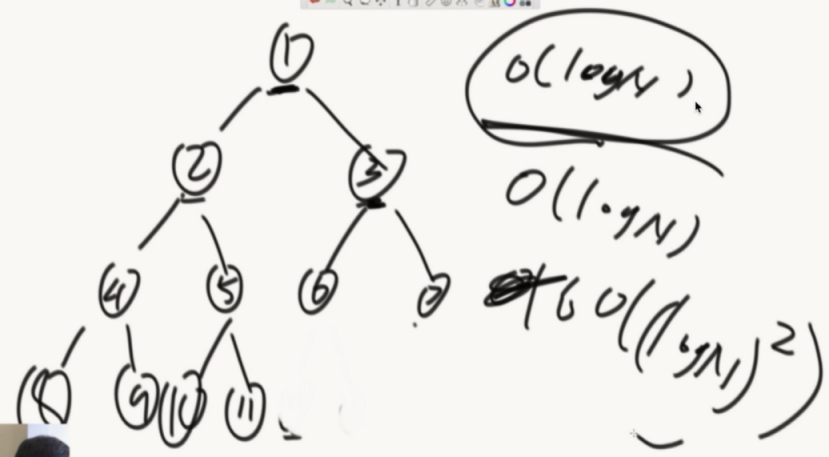
//当前节点把左边界都压栈